Знайти корінь рівняння? Це просто!
В математиці зустрічаються різноманітні рівняння. Їх завжди потрібно вирішувати, тобто шукати всі числа, які зроблять його вірним рівністю. Шляхи пошуку рішень визначаються початковим видом рівняння. Від нього залежатиме і кількість вірних значень змінної, які позначаються, як корінь рівняння. Це число може змінюватись від нуля до нескінченності.
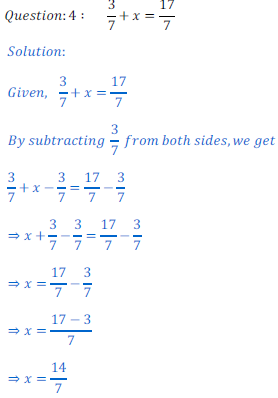
Пошук всіх можливих коренів рівняння є його рішенням. Тобто потрібно виконати ряд математичних дій, які спрощують його. А потім призводять до рівності, в якому міститься тільки невідома і яке-небудь число.
В алгебрі при вирішенні рівнянь можна прийти до такої ситуації, що коріння не буде зовсім. Тоді говорять про те, що воно нерозв'язне. А у відповіді такого рівняння треба записати, що рішень немає.
Але іноді буває і протилежне. Тобто в процесі численних перетворень з'являються сторонні корені. Вони не дадуть вірного рівності при підстановці. Тому числа завжди потрібно перевіряти, щоб уникнути ситуації з зайвими корінням у відповіді. Інакше рівняння не буде вважатися вирішеною.
Алгоритм перетворень: перенести в праву частину рівності доданок «в», замінивши його знак на протилежний; розділити обидві частини отриманої рівності на коефіцієнт «а». 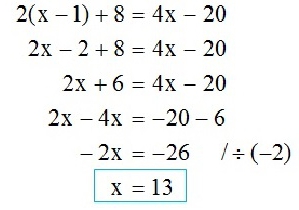
Загальний вид рішення такий:
х = -в/а .
З нього ясно, що відповіддю буде одне число. То є всього один корінь.
х 12 = (- ±Д) /(2 * а) .
Тут завжди вийде дві відповіді. Це пов'язано з тим, що у вихідній формулі стоїть знак «плюс/мінус». Він суттєво змінює значення невідомої.
При рівності «Д» нуля корінь рівняння — це єдине число. Просто тому що квадратний корінь з нуля дорівнює нулю. А значить, додавати і віднімати потрібно буде нуль. Від цього не зміниться. Тому формулу кореня рівняння можна записати без згадки "Д":
х = (- ) /(2 * а).
При від'ємному значенні спробувати витягти з неї квадратний корінь не представляється можливим. Тому коренів такого рівняння не буде. Зауваження. Це вірно для курсу шкільної програми, в якій не вивчаються комплексні числа. Коли вони вводяться, то виходить, що і в цій ситуації відповідей буде два.
х 2 + в * х + с = 0.
Тоді формула коренів квадратного рівняння зводиться до того, щоб виконати рішення двох лінійних:
х 1 + х 2 = -у
і
х 1 * х 2 = с. Воно вирішується за рахунок того, що з першого виводиться вираз для одного з коренів. І це значення потрібно підставити у друге. Так буде знайдений другий корінь, а потім перший.
До цього варіанту завжди можна прийти від загального виду квадратного рівняння. Досить тільки розділити всі коефіцієнти на «а».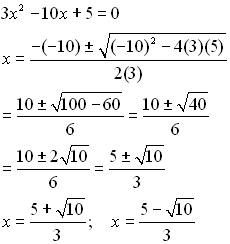
Найчастіше зустрічаються такі питання у завданнях, які мають ступінь більшу, ніж 2 або містять тригонометричні функції. Прикладом, коли потрібно знайти найменший корінь, може служити така рівність:
2 х 5 + 2 х 4 - 3 х 3 - 3 х 2 + х + 1 = 0.
Щоб знайти кожне значення, яке можна назвати "корінь рівняння", це рівність потрібно перетворити. Перша дія: згрупувати його члени попарно: перший з другим і так далі. Потім з кожної пари винести спільний множник.
В кожній дужці залишиться (х + 1). Загальним множником у першої з пар буде 2 х 4 , у другій 3-х 2 . Тепер знову потрібно виконати винесення спільного множника, яким буде однакова дужка.
Після множника (х + 1) буде стояти (2 х 4 - 3 х 2 + 1). Добуток двох множників дорівнює нулю, тільки якщо один з них приймає значення, рівне нулю. Перша дужка дорівнює нулю при х = -1. Це буде одним з коренів рівняння.
Інші будуть отримані рівняння, утвореного другий дужкою, прирівняна до нуля. Воно биквадратное. Для його вирішення потрібно ввести позначення: х 2 = у. Тоді рівняння істотно зміниться і прийме звичний вигляд квадратного рівняння. Його дискриминант дорівнює Д = 1. Він більше нуля, отже коренів буде два. Перший корінь виявляється рівним 1 другий буде 05. Але це значення для «у».
Потрібно повернутися до введеного позначенню. х 12 = ± 1 х 34 = ± 05. Всі корені рівняння: -1; 1; -05; 05. Найменший з них — -1. Це відповідь.
Якщо підставити в це рівняння замість "х" одиницю, то виходить, що 0 = 0. Цей корінь вірний.
Якщо х = -1 то виходить такий же результат. Корінь теж відповідний.
Аналогічно, при значеннях "х" рівних -05 і 05 знову виходить вірне рівність. Всі корені підходять. Цей приклад не дав сторонніх коренів. Таке буває не завжди. Цілком могло виявитися, що найменше значення не підходило б при перевірці. Тоді довелося б вибирати з тих, що залишилися. Висновок: треба пам'ятати про перевірку і уважно підходити до вирішення.
Що мається на увазі під рівнянням і його коренем?
З назви зрозуміло, що воно прирівнює дві величини, які можуть бути представлені числовими або буквеними виразами. Крім того, вони містять ще невідомі величини. Найпростіше рівняння має тільки одну. Видів рівнянь велика кількість, але поняття кореня для них завжди одне і те ж. Корінь рівняння — це таке значення невідомого числа, при якому рівняння приймає стає вірним рівністю. Бувають ситуації, коли таких чисел декілька, тоді невідома називається змінною.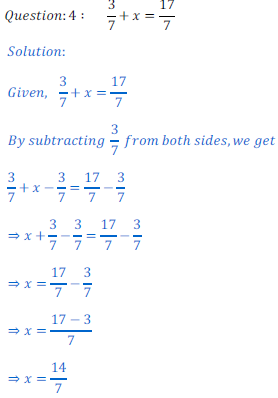
Пошук всіх можливих коренів рівняння є його рішенням. Тобто потрібно виконати ряд математичних дій, які спрощують його. А потім призводять до рівності, в якому міститься тільки невідома і яке-небудь число.
В алгебрі при вирішенні рівнянь можна прийти до такої ситуації, що коріння не буде зовсім. Тоді говорять про те, що воно нерозв'язне. А у відповіді такого рівняння треба записати, що рішень немає.
Але іноді буває і протилежне. Тобто в процесі численних перетворень з'являються сторонні корені. Вони не дадуть вірного рівності при підстановці. Тому числа завжди потрібно перевіряти, щоб уникнути ситуації з зайвими корінням у відповіді. Інакше рівняння не буде вважатися вирішеною.
Про лінійному рівнянні
Воно завжди може бути перетворено у запис наступного виду: а * х + у = 0. У ньому «а» завжди не дорівнює нулю. Щоб зрозуміти скільки коренів має рівняння, його потрібно вирішити в загальному вигляді.Алгоритм перетворень:
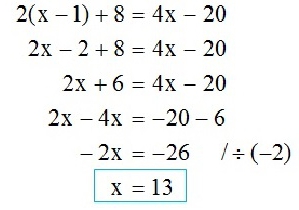
Загальний вид рішення такий:
х = -в/а .
З нього ясно, що відповіддю буде одне число. То є всього один корінь.
Квадратне рівняння
Його загальний вигляд: а * х 2 + в * х + с = 0 . Тут коефіцієнти є будь-якими числами, крім першого, «а», яке не може бути рівним нулю. Адже тоді воно автоматично перетвориться в лінійну. Відповідь на питання, скільки коренів має рівняння, вже не буде настільки однозначним, як це було в попередньому випадку. Все буде залежати від значення дискримінанта. Він обчислюється за формулою Д = в 2 - 4 а * з . Після розрахунків «Д» може бути більше, менше або рівним нулю. У першому випадку коренів рівняння буде два, у другому відповіддю буде «коренів немає», а третя ситуація дасть тільки одне значення невідомої.Формули, які використовують для знаходження коренів квадратного рівняння, містять дискриминант
У загальному випадку, коли «Д» позитивне число, не рівне нулю, потрібно використовувати таку формулу:х 12 = (- ±Д) /(2 * а) .
Тут завжди вийде дві відповіді. Це пов'язано з тим, що у вихідній формулі стоїть знак «плюс/мінус». Він суттєво змінює значення невідомої.
При рівності «Д» нуля корінь рівняння — це єдине число. Просто тому що квадратний корінь з нуля дорівнює нулю. А значить, додавати і віднімати потрібно буде нуль. Від цього не зміниться. Тому формулу кореня рівняння можна записати без згадки "Д":
х = (- ) /(2 * а).
При від'ємному значенні спробувати витягти з неї квадратний корінь не представляється можливим. Тому коренів такого рівняння не буде. Зауваження. Це вірно для курсу шкільної програми, в якій не вивчаються комплексні числа. Коли вони вводяться, то виходить, що і в цій ситуації відповідей буде два.
Формули для обчислення коренів квадратного рівняння, які не використовують дискриминант
Мова йде про теорему Вієта. Вона дійсна в разі, коли квадратне рівняння записується в дещо іншому вигляді:х 2 + в * х + с = 0.
Тоді формула коренів квадратного рівняння зводиться до того, щоб виконати рішення двох лінійних:
х 1 + х 2 = -у
і
х 1 * х 2 = с. Воно вирішується за рахунок того, що з першого виводиться вираз для одного з коренів. І це значення потрібно підставити у друге. Так буде знайдений другий корінь, а потім перший.
До цього варіанту завжди можна прийти від загального виду квадратного рівняння. Досить тільки розділити всі коефіцієнти на «а».
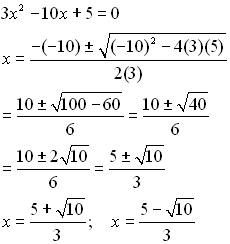
Як бути, якщо потрібно дізнатися найменше значення кореня?
Розв'язувати рівняння і знаходити всі можливі числа, які підійдуть для відповіді. А потім вибрати найменше. Це і буде найменший корінь рівняння.Найчастіше зустрічаються такі питання у завданнях, які мають ступінь більшу, ніж 2 або містять тригонометричні функції. Прикладом, коли потрібно знайти найменший корінь, може служити така рівність:
2 х 5 + 2 х 4 - 3 х 3 - 3 х 2 + х + 1 = 0.
Щоб знайти кожне значення, яке можна назвати "корінь рівняння", це рівність потрібно перетворити. Перша дія: згрупувати його члени попарно: перший з другим і так далі. Потім з кожної пари винести спільний множник.
В кожній дужці залишиться (х + 1). Загальним множником у першої з пар буде 2 х 4 , у другій 3-х 2 . Тепер знову потрібно виконати винесення спільного множника, яким буде однакова дужка.
Після множника (х + 1) буде стояти (2 х 4 - 3 х 2 + 1). Добуток двох множників дорівнює нулю, тільки якщо один з них приймає значення, рівне нулю. Перша дужка дорівнює нулю при х = -1. Це буде одним з коренів рівняння.
Інші будуть отримані рівняння, утвореного другий дужкою, прирівняна до нуля. Воно биквадратное. Для його вирішення потрібно ввести позначення: х 2 = у. Тоді рівняння істотно зміниться і прийме звичний вигляд квадратного рівняння. Його дискриминант дорівнює Д = 1. Він більше нуля, отже коренів буде два. Перший корінь виявляється рівним 1 другий буде 05. Але це значення для «у».
Потрібно повернутися до введеного позначенню. х 12 = ± 1 х 34 = ± 05. Всі корені рівняння: -1; 1; -05; 05. Найменший з них — -1. Це відповідь.
В якості висновку
Нагадування: всі рівняння потрібно перевіряти на те, чи підходить корінь. Може бути, він сторонній? Варто виконати перевірку запропонованого прикладу.Якщо підставити в це рівняння замість "х" одиницю, то виходить, що 0 = 0. Цей корінь вірний.
Якщо х = -1 то виходить такий же результат. Корінь теж відповідний.
Аналогічно, при значеннях "х" рівних -05 і 05 знову виходить вірне рівність. Всі корені підходять. Цей приклад не дав сторонніх коренів. Таке буває не завжди. Цілком могло виявитися, що найменше значення не підходило б при перевірці. Тоді довелося б вибирати з тих, що залишилися. Висновок: треба пам'ятати про перевірку і уважно підходити до вирішення.
Схожі добрі поради по темі

Закон Клапейрона-Менделєєва: формула, формулювання, використання
Кожен школяр, який навчається у десятому класі на одному з уроків фізики стикається з законом Клапейрона-Менделєєва, вивчає формули, формулювання,

Ідеальний газ. Рівняння стану ідеального газу. Ізопроцеси.
Ідеальний газ, рівняння стану ідеального газу, його температура і тиск, об'єм список параметрів і ухвал, якими оперують у відповідному розділі

Адіабатний процес, його суть та формули
Адіабатний процес (в деяких джерелах згадується як адіабатичний) - це термодинамічний процес, що відбувається при відсутності теплообміну з
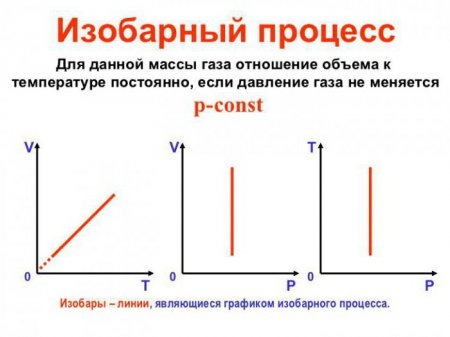
Ізобарний процес, пов'язані з ним рівняння і виведення формули роботи
Ізобарний процес (також званий изобарическим процесом) є однією з термодинамічних процесів, які відбуваються при постійному показнику тиску. Маса
Ділення на нуль. Захоплююча математика
Чому неможливо ділення на нуль, чим пояснити цей принцип елементарної математики? Як обходять цей принцип при вирішенні меж послідовностей?
Деякі моменти про те, як виконується рішення нерівностей
Одна з тем, яка вимагає від учнів максимуму уваги і посидючості, це рішення нерівностей. Такі схожі на рівняння і при цьому сильно від них