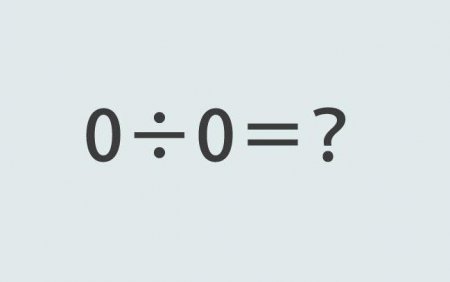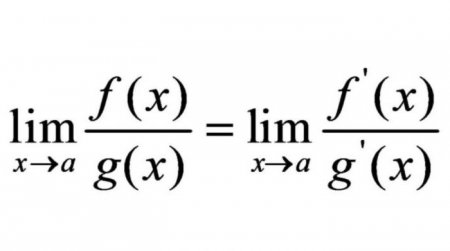Ділення на нуль. Захоплююча математика

Число 0 можна уявити як певну межу, що відокремлює світ реальних чисел від уявних чи негативних. Завдяки двозначному положення, багато операції з цією числовою величиною не підкоряються математичної логіки. Неможливість ділення на нуль – яскравий тому приклад. А дозволені арифметичні дії з нулем можуть бути виконані за допомогою загальноприйнятих визначень.

Історія нуля

Нуль є точкою відліку у всіх стандартних системах числення. Європейці стали використовувати це число порівняно недавно, але мудреці Стародавньої Індії користувалися нулем за тисячу років до того, як порожнє число стало регулярно використовуватися європейськими математиками. Ще раніше індійців нуль був обов'язковою величиною у числовій системі майя. Цей американський народ використовував дванадцятирічну систему числення, а нулем у них починався перший день кожного місяця. Цікаво, що у майя знак, що означає «нуль», повністю збігався зі знаком, що визначає «нескінченність». Таким чином, древні майя робили висновок про тотожність і непізнаваність цих величин.

Математичні дії з нулем

Стандартні математичні операції з нулем можна звести до декільком правилам. Додавання: якщо до довільного числа додати нуль, то воно не змінить свого значення (0+x=x). Віднімання: при відніманні нуля з будь-якого числа значення вичитаемого залишається незмінним (x-0=x).
Множення: будь-яке число, помножене на 0 дає у творі 0 (a*0=0). Розподіл: нуль можна розділити на будь-яке число, не рівне нулю. При цьому значення такої дробу буде 0. А ділення на нуль заборонено. Зведення в ступінь. Цю дію можна виконати з будь-яким числом. Довільне число, зведена в нульову ступінь, дасть 1 (x 0 =1). Нуль в будь ступеня дорівнює 0 (0 а =0). При цьому відразу виникає протиріччя: вираз 0 0 не має сенсу.

Парадокси математики

Про те, що поділ на нуль неможливо, багато знають зі шкільної лави. Але пояснити причину такої заборони чомусь не виходить. У насправді, чому формула ділення на нуль не існує, а от інші дії з цим числом цілком розумні і можливі? Відповідь на це питання дають математики.




Вся справа в тому, що звичні арифметичні дії, які школярі вивчають у початкових класах, насправді далеко не так рівноправні, як нам здається. Всі прості операції з числами можуть бути зведені до двох: складання і множення. Ці дії складають суть самого поняття числа, а інші операції будуються на використанні цих двох.

Додавання і множення

Візьмемо стандартний приклад на віднімання: 10-2=8. У школі його розглядають просто: якщо від десяти предметів відняти два, залишиться вісім. Але математики дивляться на цю операцію зовсім по-іншому. Адже такої операції, як віднімання, для них не існує. Даний приклад можна записати й іншим способом: х+2=10. Для математиків невідома різниця – це просто число, яке треба додати до двох, щоб вийшло вісім. І ніякого віднімання тут не потрібно, потрібно просто знайти відповідне числове значення. Множення і ділення розглядаються так само. У прикладі 12:4=3 можна зрозуміти, що мова йде про поділ восьми предметів на дві рівні кучки. Але насправді це просто перевернута формула запису 3х4=12.Такі приклади на ділення можна наводити нескінченно.

Приклади ділення на 0

Ось тут і потроху стає зрозумілим, чому не можна ділити на нуль. Множення і ділення на нуль підпорядковується своїм правилам. Всі приклади на ділення цієї величини можна сформулювати у вигляді 6:0=х. Але це ж перевернута запис виразу 6 * х=0. Але, як відомо, будь-яке число, помножене на 0 дає у творі лише 0. Це властивість закладено в самому понятті нульової величини. Виходить, що такого числа, яке при множенні на 0 дає якусь відчутну величину, не існує, тобто дана задача не має рішення. Такої відповіді боятися не слід, це природна відповідь для задач такого типу. Просто запис 6:0 не має ніякого сенсу, і вона нічого не може пояснити. Коротко кажучи, цей вираз можна пояснити тим самим безсмертним «ділення на нуль неможливо». Існує операція 0:0? Дійсно, якщо операція множення на 0 законна, можна нуль поділити на нуль? Адже рівняння види 0х 5=0 цілком легально. Замість числа 5 можна поставити 0 твір від цього не зміниться. Дійсно, 0х0=0. Але поділити на 0 і раніше не можна. Як було сказано, поділ – це просто зворотна операція множення. Таким чином, якщо в прикладі 0х5=0 потрібно визначити другий множник, отримуємо 0х0=5. Або 10. Або нескінченність. Поділ нескінченності на нуль — як вам це сподобається? Але якщо у вираз підходить будь-яке число, то воно не має сенсу, ми не можемо з нескінченного безлічі чисел вибрати якусь одну. А раз так, це значить і вираз 0:0 не має сенсу. Виходить, що на нуль не можна ділити навіть сам нуль.

Вища математика

Ділення на нуль — це головний біль для шкільної математики. Досліджуваний в технічних вузах математичний аналіз трохи розширює поняття завдань, які не мають рішення. Наприклад, до вже відомим висловом 0:0 додаються нові, які не мають рішення в шкільних курсах математики:

нескінченність, розділена на нескінченність: :;

нескінченність мінус нескінченність: -;

одиниця, зведена в нескінченну ступінь: 1 ;

нескінченність, помножена на 0: *0;

деякі інші.

Елементарними методами вирішити такі вирази неможливо. Але вища математика завдяки додатковим можливостям для ряду подібних прикладів дає кінцеві рішення. Особливо це видно у розгляді завдань з теорії меж.

Розкриття невизначеності

В теорії меж значення 0 замінюється умовної нескінченно малої змінною величиною. А вирази, в яких при подставлении потрібного значення виходить ділення на нуль, перетворюються. Нижче представлений стандартний приклад розкриття межі за допомогою звичайних алгебраїчних перетворень: Як видно у прикладі, просте скорочення дробу приводить її значення до цілком раціональному відповіді. При розгляді меж тригонометричних функцій їх вираження прагнуть звести до першого чудовому межі. При розгляді меж, в яких знаменник звертається до 0 при подставлении межі, використовують другий чудовий межа.

Метод Лопіталя

У деяких випадках межі виразів можна замінити межею їх похідних. Гійом Лопиталь – французький математик, основоположник французької школи математичного аналізу. Він довів, що межі виразів рівні меж похідних цих виразів. В математичній запису правило виглядає наступним чином. В даний час метод Лопіталя з успіхом застосовується при вирішенні невизначеностей типу 0:0 або :.