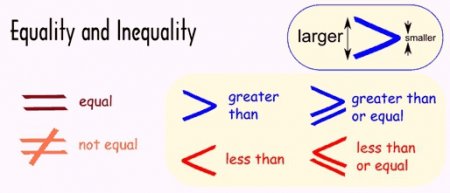
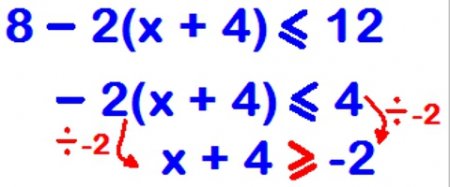Деякі моменти про те, як виконується рішення нерівностей
Одна з тем, яка вимагає від учнів максимуму уваги і посидючості, це рішення нерівностей. Такі схожі на рівняння і при цьому сильно від них відрізняються. Тому що до їх вирішення потрібен особливий підхід. Функцію, яка визначена в ОДЗ, або будь-який число можна додати до обох частин вихідного нерівності. Аналогічним чином можливо множення, але тільки на позитивну функцію або число. Якщо ця дія виконується з негативними функцією або числом, то знак нерівності потрібно замінити на протилежний. Функції, які є неотрицательними, можна зводити в позитивну ступінь.
Іноді рішення нерівностей супроводжується діями, які дають сторонні відповіді. Їх потрібно виключити, порівнявши область ОДЗ і безліч рішень.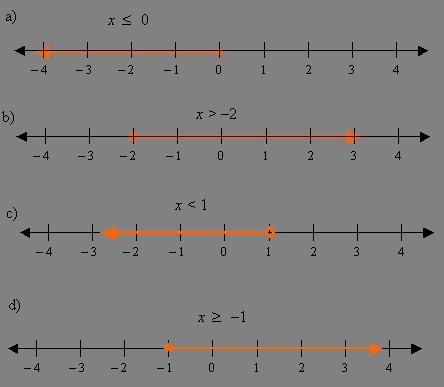
Визначити область, де лежать допустимі значення змінних, тобто ОДЗ. Перетворити нерівність за допомогою математичних операцій так, щоб у його правій частині стояв нуль. Знак нерівності замінити на «=» і вирішити відповідне рівняння. На числовій осі відзначити всі відповіді, які вийшли під час вирішення, а також інтервали ОДЗ. При строгому нерівність точки потрібно намалювати виколотими. Якщо присутній знак рівності, то їх належить зафарбувати. Визначити знак вихідної функції на кожному інтервалі, отриманому з точок ОДЗ і ділять його відповідей. Якщо при переході через точку знак функції не змінюється, то вона входить у відповідь. В противному разі — відкидається. Граничні для ОДЗ точки потрібно додатково перевірити і тільки потім включати чи ні у відповідь. Відповідь, який виходить, потрібно записати у вигляді об'єднаних множин.
Для їх вирішення також допустимо використовувати властивості, зазначені вище. З їх допомогою зручно приводити нерівності до рівності нулю. |х| < a на -a < х < a; |x| > a на х a. Якщо нерівності несуворі, то формули теж вірні, тільки в них, крім знака більше або менше, з'являється «=».
План, за яким виконується рішення системи нерівностей: вирішити кожне з них окремо; зобразити на числовій осі всі інтервали і визначити їх перетину; записати відповідь системи, який і буде об'єднанням того, що вийшло у другому пункті. Використовуючи описані властивості, надати дробу такий вигляд, щоб праворуч від знака залишився тільки нуль. Замінити нерівність «=» і визначити точки, в яких функція дорівнює нулю. Відзначити їх на координатній осі. При цьому числа, отримані в результаті розрахунків у знаменнику, завжди будуть виколоті. Всі інші — виходячи з умови нерівності. Визначити проміжки знакопостоянства. У відповідь записати об'єднання тих проміжків, знак яких відповідає тому, який був у вихідному нерівність.
Вихідне нерівність
умова
равносильная система
n(х) (m(х)) 2
або n(х) більше або дорівнює 0 m(х) менше 0
n(x) = (m(х)) 2
або n(х) більше або дорівнює 0 m(х) менше 0
n(х) < √ m(х)
n(х) більше або дорівнює 0 n(х) менше m(х)
n(х) * m(х) 0
n(х) більше 0 m(х) більше 0
n(х) * m(х) =0
або n(х) дорівнює 0 m(х) –будь
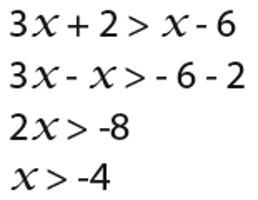 Другий приклад. Потрібно вирішити систему двох рівнянь: 3х + 3 <= 2х + 1 і 3х - 2 <= 4х + 2. Рішення. ОДЗ цих нерівностей теж лежить в області будь-яких чисел, оскільки дані лінійні функції. Далі потрібно діяти поетапно. Спочатку перетворити перше з нерівностей і прирівняти її до нуля. 3х + 3 - 2х - 1 = 0. Тобто х + 2 = 0. Таким чином, х дорівнює -2. Друге нерівність прийме вигляд такого рівняння: 3х - 2 - 4х - 2 = 0. Після перетворення: -х - 4 =0. З нього виходить значення для змінної, рівне -4. Ці два числа потрібно відзначити на осі, зобразивши інтервали. Оскільки нерівність нестроге, то всі точки потрібно зафарбувати. Перший інтервал від мінус нескінченності до -4. Нехай буде вибрано число -5. Перше нерівність дасть значення -3 а друге 1. Значить, цей проміжок не входить у відповідь. Другий інтервал від -4 до -2. Можна вибрати число -3 і підставити його в обидва нерівності. У першому і у другому виходить значення -1. Отже, під дугою «-». На останньому інтервалі від -2 до нескінченності найкращим числом є нуль. Його і потрібно підставити і знайти значення нерівностей. У першому з них виходить додатне число, а другому нуль. Цей проміжок теж потрібно виключити з відповіді. З трьох інтервалів рішенням нерівності є тільки один. Відповідь: х належить[-4; -2]. Третій приклад. |1 - х| > 2 |х - 1|. Рішення. Насамперед потрібно визначити точки, які звертаються в нуль. Для лівого цим числом 2 для правого — 1. їх потрібно зазначити на промені і визначити проміжки знакопостоянства. На першому інтервалі від мінус нескінченності до 1 функція з лівої частини нерівності приймає позитивні значення, а з правої — негативні. Під дугою потрібно записати поруч два знаки «+» і «-». Наступний проміжок від 1 до 2. На ньому обидві функції приймають позитивні значення. Отже, під дугою два плюси. Третій інтервал від 2 до нескінченності дасть такий результат: ліва функція — негативна, права — позитивна. З урахуванням одержаних знаків потрібно обчислити значення нерівності для всіх проміжків. На першому виходить така нерівність: 2 - х > - 2 (х - 1). Мінус перед двійкою у другому нерівність вийшов з-за того, що ця функція негативна. Після перетворення нерівність виглядає так: х > 0. Воно відразу дає значення змінної. Тобто з цього інтервалу у відповідь піде тільки проміжок від 0 до 1. На другому: 2 - х > 2 (х - 1). Перетворення дадуть таку нерівність: -3х + 4 більше нуля. Його нулем значення х = 4/3. З урахуванням знака нерівності виходить, що х повинен бути менше цього числа. Значить, цей інтервал зменшується до проміжку від 1 до 4/3. Останній дає таку запис нерівності: - (2 - х) > 2 (х - 1). Його перетворення призводить до такого: -х > 0. Тобто рівняння вірно при х меншому нуля. Це означає, що на шуканому проміжку нерівність не дає рішень. На перших двох проміжках граничним виявилося число 1. Його потрібно перевірити окремо. Тобто підставити у вихідне нерівність. Виходить: |2 - 1| > 2 |1 - 1|. Підрахунок дає більше 1 0. Це вірне твердження, тому одиниця входить у відповідь. Відповідь: х лежить в проміжку (0; 4/3).
Другий приклад. Потрібно вирішити систему двох рівнянь: 3х + 3 <= 2х + 1 і 3х - 2 <= 4х + 2. Рішення. ОДЗ цих нерівностей теж лежить в області будь-яких чисел, оскільки дані лінійні функції. Далі потрібно діяти поетапно. Спочатку перетворити перше з нерівностей і прирівняти її до нуля. 3х + 3 - 2х - 1 = 0. Тобто х + 2 = 0. Таким чином, х дорівнює -2. Друге нерівність прийме вигляд такого рівняння: 3х - 2 - 4х - 2 = 0. Після перетворення: -х - 4 =0. З нього виходить значення для змінної, рівне -4. Ці два числа потрібно відзначити на осі, зобразивши інтервали. Оскільки нерівність нестроге, то всі точки потрібно зафарбувати. Перший інтервал від мінус нескінченності до -4. Нехай буде вибрано число -5. Перше нерівність дасть значення -3 а друге 1. Значить, цей проміжок не входить у відповідь. Другий інтервал від -4 до -2. Можна вибрати число -3 і підставити його в обидва нерівності. У першому і у другому виходить значення -1. Отже, під дугою «-». На останньому інтервалі від -2 до нескінченності найкращим числом є нуль. Його і потрібно підставити і знайти значення нерівностей. У першому з них виходить додатне число, а другому нуль. Цей проміжок теж потрібно виключити з відповіді. З трьох інтервалів рішенням нерівності є тільки один. Відповідь: х належить[-4; -2]. Третій приклад. |1 - х| > 2 |х - 1|. Рішення. Насамперед потрібно визначити точки, які звертаються в нуль. Для лівого цим числом 2 для правого — 1. їх потрібно зазначити на промені і визначити проміжки знакопостоянства. На першому інтервалі від мінус нескінченності до 1 функція з лівої частини нерівності приймає позитивні значення, а з правої — негативні. Під дугою потрібно записати поруч два знаки «+» і «-». Наступний проміжок від 1 до 2. На ньому обидві функції приймають позитивні значення. Отже, під дугою два плюси. Третій інтервал від 2 до нескінченності дасть такий результат: ліва функція — негативна, права — позитивна. З урахуванням одержаних знаків потрібно обчислити значення нерівності для всіх проміжків. На першому виходить така нерівність: 2 - х > - 2 (х - 1). Мінус перед двійкою у другому нерівність вийшов з-за того, що ця функція негативна. Після перетворення нерівність виглядає так: х > 0. Воно відразу дає значення змінної. Тобто з цього інтервалу у відповідь піде тільки проміжок від 0 до 1. На другому: 2 - х > 2 (х - 1). Перетворення дадуть таку нерівність: -3х + 4 більше нуля. Його нулем значення х = 4/3. З урахуванням знака нерівності виходить, що х повинен бути менше цього числа. Значить, цей інтервал зменшується до проміжку від 1 до 4/3. Останній дає таку запис нерівності: - (2 - х) > 2 (х - 1). Його перетворення призводить до такого: -х > 0. Тобто рівняння вірно при х меншому нуля. Це означає, що на шуканому проміжку нерівність не дає рішень. На перших двох проміжках граничним виявилося число 1. Його потрібно перевірити окремо. Тобто підставити у вихідне нерівність. Виходить: |2 - 1| > 2 |1 - 1|. Підрахунок дає більше 1 0. Це вірне твердження, тому одиниця входить у відповідь. Відповідь: х лежить в проміжку (0; 4/3).
Властивості, які потрібні для знаходження відповіді
Всі вони застосовуються для того, щоб замінити наявну запис рівносильною. Велика їх частина схожа на те, що було в рівняннях. Але є і відмінності.Іноді рішення нерівностей супроводжується діями, які дають сторонні відповіді. Їх потрібно виключити, порівнявши область ОДЗ і безліч рішень.
Використання методу інтервалів
Його суть полягає в тому, щоб звести нерівність до рівняння, в якому у правій частині стоїть нуль.
Трохи про подвійні нерівностях
Вони використовують у запису відразу два знаку нерівності. Тобто деяка функція обмежена умовами відразу двічі. Такі нерівності розв'язуються, як система з двох, коли вихідне розбито на частини. І в методі інтервалів зазначаються відповіді від рішення обох рівнянь.Для їх вирішення також допустимо використовувати властивості, зазначені вище. З їх допомогою зручно приводити нерівності до рівності нулю.
Як йдуть справи з нерівностей, у яких є модуль?
У цьому випадку рішення нерівностей використовує такі властивості, причому вони справедливі для позитивного значення «а». Якщо «х» приймає алгебраїчний вираз, то справедливі такі заміни:Як здійснюється рішення системи нерівностей?
Це знання буде потрібно в тих випадках, коли дано таке завдання або є запис подвійного нерівності або в запису з'явився модуль. У такій ситуації рішенням будуть такі значення змінних, які задовольняли б усіх наявних в запису нерівностям. Якщо таких чисел немає, то система розв'язків не має.План, за яким виконується рішення системи нерівностей:
Як бути з дробовими нерівностей?
Оскільки під час їх вирішення може знадобитися зміна знаку нерівності, то потрібно дуже ретельно і уважно виконувати всі пункти плану. Інакше може вийти протилежний відповідь. Рішення дрібних нерівностей теж використовує метод інтервалів. І план дій буде таким:Ситуації, коли у нерівності з'являється ірраціональність
Іншими словами, в запису присутній математичний корінь. Оскільки в шкільному курсі алгебри велика частина завдань йде для квадратного кореня, то саме він і буде розглянуто. Рішення ірраціональних нерівностей зводиться до того, щоб отримати систему з двох або трьох, які будуть рівносильні вихідного.Вихідне нерівність
умова
равносильная система
n(х) (m(х)) 2
або n(х) більше або дорівнює 0 m(х) менше 0
n(x) = (m(х)) 2
або n(х) більше або дорівнює 0 m(х) менше 0
n(х) < √ m(х)
n(х) більше або дорівнює 0 n(х) менше m(х)
n(х) * m(х) 0
n(х) більше 0 m(х) більше 0
n(х) * m(х) =0
або n(х) дорівнює 0 m(х) –будь
Приклади розв'язання різних видів нерівностей
Для того, щоб додати наочності в теорію про рішення нерівностей, нижче наведено приклади. Перший приклад. 2х - 4 > 1 + х Рішення: для того щоб визначити ОДЗ, достатньо просто уважно подивитися на нерівність. Воно утворене з лінійних функцій, тому визначена при всіх значеннях змінної. Тепер з обох частин нерівності треба відняти (1 + х). Виходить: 2х - 4 - (1 + х) > 0. Після того як будуть розкриті дужки і наведені подібні доданки нерівність прийме такий вигляд: х - 5 > 0. Прирівнявши його до нуля, легко знайти його рішення: х = 5. Тепер цю точку з цифрою 5 потрібно відзначити на координатному промені. Потім перевірити знаки вихідної функції. На першому інтервалі від мінус нескінченності до 5 можна взяти число 0 і підставити його в нерівність, що вийшло після перетворень. Після розрахунків виходить -7 >0. під дугою інтервалу потрібно підписати знак мінуса. На наступному інтервалі від 5 до безкінечності можна вибрати число 6. Тоді виходить, що 1 > 0. Під дугою підписаний знак «+». Цей другий інтервал і буде відповіддю нерівності. Відповідь: х лежить в інтервалі (5; ).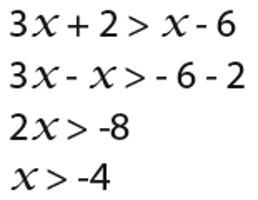
Схожі добрі поради по темі

Ідеальний газ. Рівняння стану ідеального газу. Ізопроцеси.
Ідеальний газ, рівняння стану ідеального газу, його температура і тиск, об'єм список параметрів і ухвал, якими оперують у відповідному розділі
Ділення на нуль. Захоплююча математика
Чому неможливо ділення на нуль, чим пояснити цей принцип елементарної математики? Як обходять цей принцип при вирішенні меж послідовностей?
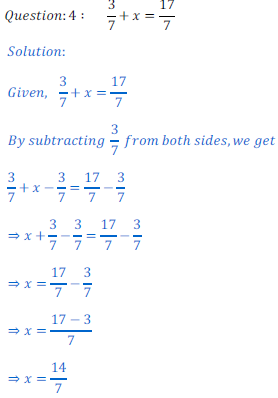
Знайти корінь рівняння? Це просто!
В математиці зустрічаються різноманітні рівняння. Їх завжди потрібно вирішувати, тобто шукати всі числа, які зроблять його вірним. Шляхи пошуку
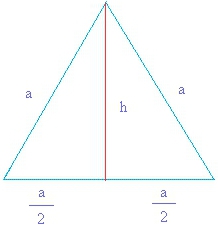
Як дізнатися площу рівностороннього трикутника: основні формули
Знайти площу рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована
Комплексні числа та дії над ними
Комплексні числа не є числами в елементарному значенні цього слова, що застосовуються при підрахунках і вимірюваннях, а є математичними об'єктами,
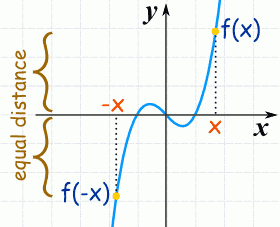
Як провести повне дослідження функції
У цій статті розглянемо план повного дослідження функції, а також наведемо приклади дослідження функції на екстремум, монотонність, асимптоти.