Як провести повне дослідження функції
У цій статті розглянемо схему дослідження функції, а також наведемо приклади дослідження на екстремуми, монотонність, асимптоти даної функції. Область існування (ОДЗ) функції. Перетин функції (якщо є) з осями координат, знаки функції, парність, періодичність. Точки розриву (їх рід). Безперервність. Вертикальні асимптоти. Монотонність і точки екстремуму. Точки перегину. Опуклість. Дослідження функції на нескінченності, на асимптоти: горизонтальні та похилі. Побудова графіка.
 Приклад: y = 1 : 3x 3 – 6 : 2x 2 + 5x. ОДЗ: хєR y' = x 2 + 6x + 5.
Приклад: y = 1 : 3x 3 – 6 : 2x 2 + 5x. ОДЗ: хєR y' = x 2 + 6x + 5.
Знайдемо проміжки постійних знаків y' . Оскільки y' - елементарна функція, то вона може змінювати знаки тільки в точках, де вона перетворюється в нуль або не існує. Її ОДЗ: хєR . Знайдемо точки, похідна в яких дорівнює 0 (нулю): y' = 0; x = -1; -5. Отже, y зростаюча на (-; -5] і на [-1; +∞), y нисходящая на [1; 2] .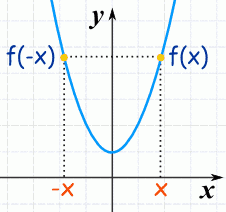 Теорема (необхідна умова). Якщо x 0 - точка екстремуму (локального) функції g , то похідна не існує або дорівнює в цій т. 0 (нулю). Визначення. Критичними називають точки з неіснуючої або дорівнює 0 (нулю) похідної. Саме дані точки підозрілі на екстремум. Теорема (достатня умова № 1). Якщо функція g неперервна в деякому окрузі т. x 0 і знак змінює через цю точку похідна при переході, то дана точка є т. екстремуму g . Теорема (достатня умова № 2). Нехай функція в деякій окрузі точки диференційовних двічі і g' = 0 а g > 0 (g" < 0) , тоді ця точка є точкою максимуму (max) або мінімуму (min) функції.
Теорема (необхідна умова). Якщо x 0 - точка екстремуму (локального) функції g , то похідна не існує або дорівнює в цій т. 0 (нулю). Визначення. Критичними називають точки з неіснуючої або дорівнює 0 (нулю) похідної. Саме дані точки підозрілі на екстремум. Теорема (достатня умова № 1). Якщо функція g неперервна в деякому окрузі т. x 0 і знак змінює через цю точку похідна при переході, то дана точка є т. екстремуму g . Теорема (достатня умова № 2). Нехай функція в деякій окрузі точки диференційовних двічі і g' = 0 а g > 0 (g" < 0) , тоді ця точка є точкою максимуму (max) або мінімуму (min) функції.
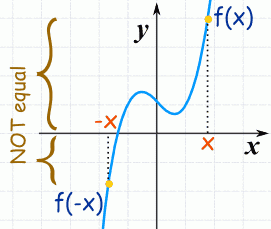 Функція буде строго опуклою вниз на (а, b) , якщо - графік лежить нижче січної на проміжку. Функцію називають опуклою вгору (опуклою) на проміжку (а, b) якщо для будь-т очек з (а, b) графік функції на проміжку лежить не нижче січної, що проходить через абсциси в цих точках . Функція строго опуклою вгору на (а, b ), якщо - графік на проміжку лежить вище січною. Якщо функція у деякому окрузі точки неперервна і через т. x 0 при переході функція змінює опуклість то ця точка називається точкою перегину функції.
Функція буде строго опуклою вниз на (а, b) , якщо - графік лежить нижче січної на проміжку. Функцію називають опуклою вгору (опуклою) на проміжку (а, b) якщо для будь-т очек з (а, b) графік функції на проміжку лежить не нижче січної, що проходить через абсциси в цих точках . Функція строго опуклою вгору на (а, b ), якщо - графік на проміжку лежить вище січною. Якщо функція у деякому окрузі точки неперервна і через т. x 0 при переході функція змінює опуклість то ця точка називається точкою перегину функції.
План Знайти похідну g'(x) . Шукати значення функції g в цих точках і на кінцях відрізка. Знайдені значення порівняти і вибрати найменше та найбільше. Зауваження. Якщо потрібно провести дослідження функції на кінцевому інтервалі (а, b) , або на нескінченному (-; b); (-; +) на max і min значення, то в плані замість значень функції на кінцях проміжку шукають відповідні односторонні границі: замість f(a) шукають f(a+) = limf(x) замість f(b) шукають f(-b) . Так можна знайти ОДЗ функції на проміжку, тому що абсолютні екстремуми не обов'язково існують в даному випадку. Виражають цю величину через інші величини з умови задачі так, щоб вона була функцією тільки від однієї змінної (якщо це можливо). Визначають проміжок зміни цієї змінної. Проводять дослідження функції на проміжку на max і min значення. Завдання. Потрібно побудувати майданчик прямокутної форми, використавши а метрів сітки, біля стіни так, щоб з одного боку вона прилягала до стіни, а з інших трьох була огороджена сіткою. При якому співвідношенні сторін площа такого майданчика буде найбільшою? S = xy функція 2 змінних. S = x(a - 2x) - функція 1-ї змінної ; x є [0; a:2]. S = ax - 2x 2 ; S' = a - 4x = 0 xєR, x = a : 4. S(a : 4) = a 2 : 8 - найбільше значення; S(0) =0. Знайдемо іншу сторону прямокутника: у = a : 2. Співвідношення сторін: y : x = 2. Відповідь. Найбільша площа дорівнюватиме a 2 /8 якщо сторона , яка паралельна стіні, в 2 рази більше іншого боку.
ОДЗ: хє(-; 1) U (1; ). Загального вигляду функція ні парна, ні непарна), відносно точки 0 (нуль) не симетрична. Знаки функції. Елементарна функція, тому може змінювати знак тільки в точках, де вона дорівнює 0 (нулю), або не існує. Елементарна функція, тому неперервна на ОДЗ: (-; 1) U (1; ). Розрив: х = 1; limx 3 : (1 - x) 2 = - Розрив 2-го роду (нескінченний), тому є вертикальна асимптота в точці 1; х = 1 - рівняння вертикальної асимптоти. 5. y' = x 2 (3 - x) : (1 - x) 3 ; ОДЗ (y'): x /= 1; х = 1 - критична точка. y' = 0; 0; 3 - критичні точки. 6. y" = 6x : (1 - x) 4 ; Критичні т.: 1 0; x = 0 - т. перегину, y(0) = 0. 7. limx 3 : (1 - 2x + x 2 ) = - немає горизонтальної асимптоти, але може бути похила. k = 1 – число; b = 2 – число. Отже, є похила асимптота y = x + 2 на + і на - . Приклад 2 Дано y = (x 2 + 1) : (x - 1). Провести і сследованіе. Побудувати графік.
1. Область існування - вся числова пряма, крім т. x = 1 .
2. y перетинає OY (якщо це можливо) в т. (0;g(0)) . Знаходимо y(0) = -1 - т. перетину OY . Точки перетину графіка з OX знаходимо, розв'язавши рівняння y = 0 . Рівняння дійсних коренів не має, тому ця функція не перетинає OX .
3. Функція неперіодична. Розглянемо вираз
g(-x) /= g(x) і g(-x) /= g(x) . Це означає, що це функція загального виду (ні парна, ні непарна).
4. Т. x = 1 розрив має другого роду. У всіх інших точках функція неперервна.
5. Дослідження функції на екстремум: (x 2 - 2x - 1) : (x - 1) 2 = y' і вирішимо рівняння y' = 0. Отже, 1 - 2 1 + 2 1 - критичні точки або точки можливого екстремуму. Ці точки розбивають числову пряму на чотири інтервалу .
На кожному інтервалі похідна має певний знак, який можна встановити методом інтервалів або обчислення значень похідної в окремих точках. На інтервалах (-; 1 - 2 ) U ( 1 + 2 ; ) , позитивна похідна, отже, функція зростає; якщо хє ( 1 - 2 ; 1) U (1; 1 + 2 ) , то функція убуває, тому що на цих інтервалах похідна негативна. Через т. x 1 при переході (рух слід зліва направо) похідна змінює знак з "+" на "-", тому в цій точці має локальний максимум, знайдемо
y max = 2 - 2 2 .
При переході через x 2 похідна змінює знак з "-" на "+", тому в цій точці має локальний мінімум, причому
y mix = 2 + 22.
Т. x = 1 не т. екстремуму.
6. 4 : (x - 1) 3 = y". На (-; 1 ) 0 > y" , слідчо, на цьому інтервалі крива опукла; якщо хє ( 1 ; ) - крива вгнута. В т очке 1 не визначена функція, тому ця точка не точка перегину.
7. З результатів пункту 4 слід, що x = 1 - вертикальна асимптота кривої.
Горизонтальні асимптоти відсутні.
x + 1 = y - похила асимптота даної кривої. Інших асимптот немає.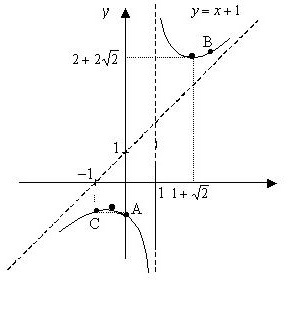 8. Враховуючи проведені дослідження, будуємо графік (см. малюнок вище).
8. Враховуючи проведені дослідження, будуємо графік (см. малюнок вище).
Схема
Дослідження на монотонність
Теорема. Якщо функція g неперервна на [a, b] , диференційована на (а; b) і g'(x) >= 0 (g'(x)<=0) , хє(а; b) , то g зростаюча (спадна) на [a, b] .
Знайдемо проміжки постійних знаків y' . Оскільки y' - елементарна функція, то вона може змінювати знаки тільки в точках, де вона перетворюється в нуль або не існує. Її ОДЗ: хєR . Знайдемо точки, похідна в яких дорівнює 0 (нулю): y' = 0; x = -1; -5. Отже, y зростаюча на (-; -5] і на [-1; +∞), y нисходящая на [1; 2] .
Дослідження на екстремум
Т. x 0 називають точкою максимуму (max) на множині А функції g тоді, коли приймається в цій точці функцією найбільше значення g(x 0 ) >= g(x), хєА . Т. x 0 називають точкою мінімуму (min) функції g на множині А тоді, коли приймається в цій точці функцією значення найменшу g(x 0 ) <= g(x), хєА. На множині А точки максимуму (max) і мінімуму (min) іменуються точками екстремуму g . Такі екстремуми ще називають абсолютними екстремумами на множині . Якщо x 0 - точка екстремуму функції g у певному своєму окрузі, то x 0 називається точкою локального або місцевого екстремуму (max або min) функції g.
Дослідження на опуклість
Функцію називають опуклою вниз (або увігнутою) на інтервалі (а, b) тоді, коли графік функції розташований не вище січної на проміжку для будь-яких x з (а, b) , яка проходить через ці точки .
Дослідження на асимптоти
Визначення. Пряму називають асимптотой g(x) якщо при нескінченному відстані від початку координат до неї наближається точка графіка функції: d(M,l). Асимптоти можуть бути вертикальні, горизонтальні і похилі. Вертикальна пряма з рівнянням x = x 0 буде асимптотой вертикальної графіка функції g якщо в т. x 0 нескінченний розрив, тобто хоча б одна ліва або права межа в цій точці - нескінченність.Дослідження функції на відрізку значення найменше та найбільше
Якщо функція неперервна на [a, b] , то за теоремою Вейєрштрасса існує значення найбільше і найменше значення на цьому відрізку, тобто існують т окуляри, які належать [a, b] такі, що g(x 1 ) <= g(x) < g(x 2 ), x 2 є[a, b]. З теореми про монотонність та екстремуми отримуємо наступну схему дослідження функції на відрізку на найменше та найбільше значення.План
Застосування похідної до розв'язування прикладних задач на екстремум деяких величин
Дослідження функції. Приклади
Приклад 1 Є y=x 3 : (1-x) 2 . Провести дослідження.1. Область існування - вся числова пряма, крім т. x = 1 .
2. y перетинає OY (якщо це можливо) в т. (0;g(0)) . Знаходимо y(0) = -1 - т. перетину OY . Точки перетину графіка з OX знаходимо, розв'язавши рівняння y = 0 . Рівняння дійсних коренів не має, тому ця функція не перетинає OX .
3. Функція неперіодична. Розглянемо вираз
g(-x) /= g(x) і g(-x) /= g(x) . Це означає, що це функція загального виду (ні парна, ні непарна).
4. Т. x = 1 розрив має другого роду. У всіх інших точках функція неперервна.
5. Дослідження функції на екстремум: (x 2 - 2x - 1) : (x - 1) 2 = y' і вирішимо рівняння y' = 0. Отже, 1 - 2 1 + 2 1 - критичні точки або точки можливого екстремуму. Ці точки розбивають числову пряму на чотири інтервалу .
На кожному інтервалі похідна має певний знак, який можна встановити методом інтервалів або обчислення значень похідної в окремих точках. На інтервалах (-; 1 - 2 ) U ( 1 + 2 ; ) , позитивна похідна, отже, функція зростає; якщо хє ( 1 - 2 ; 1) U (1; 1 + 2 ) , то функція убуває, тому що на цих інтервалах похідна негативна. Через т. x 1 при переході (рух слід зліва направо) похідна змінює знак з "+" на "-", тому в цій точці має локальний максимум, знайдемо
y max = 2 - 2 2 .
При переході через x 2 похідна змінює знак з "-" на "+", тому в цій точці має локальний мінімум, причому
y mix = 2 + 22.
Т. x = 1 не т. екстремуму.
6. 4 : (x - 1) 3 = y". На (-; 1 ) 0 > y" , слідчо, на цьому інтервалі крива опукла; якщо хє ( 1 ; ) - крива вгнута. В т очке 1 не визначена функція, тому ця точка не точка перегину.
7. З результатів пункту 4 слід, що x = 1 - вертикальна асимптота кривої.
Горизонтальні асимптоти відсутні.
x + 1 = y - похила асимптота даної кривої. Інших асимптот немає.

Схожі добрі поради по темі

Що таке полюс? Визначення
У даній статті будуть розглянуті проблеми тлумачення слова полюс. Значень, в принципі, досить багато. У широкому розумінні цим терміном позначається
Немембранні всіх органел клітини: види, будова, функції
Якими бувають всіх органел клітини? Як влаштовані мембранні та немембранні всіх органел? Які функції виконує кожен з них?
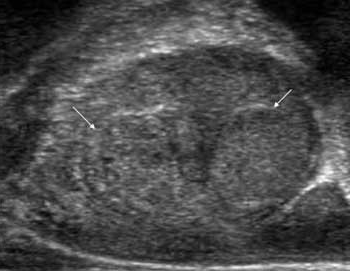
УЗД простати: підготовка, як робиться
Один з методів, що дозволяють оцінити стан передміхурової залози - це УЗД простати. Завдяки йому можна виявити патології сечостатевої системи, а
Деякі моменти про те, як виконується рішення нерівностей
Одна з тем, яка вимагає від учнів максимуму уваги і посидючості, це рішення нерівностей. Такі схожі на рівняння і при цьому сильно від них
Інформаційно-пошукові системи: Nigma та її особливості
Можна сказати, що інформаційно-пошукові системи дуже цікаве явище. Однією з найбільш досконалих серед них в нашій країні можна назвати проект Nigma.

Автомобільні високовольтні дроти: функції і призначення
Високовольтні дроти використовуються в системі запалювання автомобілів. Їх основна функція - передача електричних імпульсів від котушки запалювання