Як дізнатися площу рівностороннього трикутника: основні формули
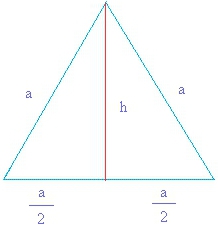
Знайти площа рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована особливість саме цієї фігури і математичні вирази суттєво спрощені. Перший випадок тільки вимагає заміни всіх сторін однаковим значенням і врахування того, що всі кути трикутника рівні 60o. Потім залишиться провести нескладні перетворення, які і приведуть до формул, даними в готовому вигляді трохи нижче.
Величина
Її позначення
сторона
а
площа
S
висота
н
радіуси кіл вписаної та описаної
r і R, відповідно
Розрахунок площі трикутника в цьому випадку буде здійснюватися за формулою: S = 3/4 * а 2 . Вона легко виходить з тієї, яка відома для довільної фігури з трьома сторонами. Просто у формулі потрібно врахувати те, що всі сторони трикутника рівні. Якщо говорити більш точно, то потрібно формула Герона: S = (p(p-a)(p-b)(p-c)). Значення полупериметра для рівностороннього трикутника буде одно 3а/2. Таким чином, в кожній дужці під коренем вийде вираз(3а/2) - а). Воно дасть після перетворення а/2.
Так як дужок три, то у цього виразу з'явиться третя ступінь. А значить, воно перетвориться в а 3 /8. Його ще потрібно помножити на півпериметр, який визначається як сума сторін, розділена на 2. Вийде вираз: 3а 4 /16. Після вилучення квадратного кореня як раз і залишиться той вираз, що дано у першій формулі для площі рівностороннього трикутника.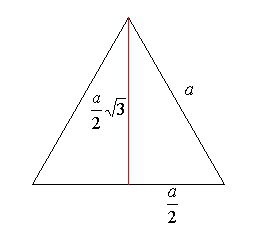 Тому немає необхідності запам'ятовувати багато формул. Можна просто запам'ятати одну — Герона. З неї шляхом простих математичних перетворень виходять всі інші, наприклад, для рівностороннього трикутника.
Тому немає необхідності запам'ятовувати багато формул. Можна просто запам'ятати одну — Герона. З неї шляхом простих математичних перетворень виходять всі інші, наприклад, для рівностороннього трикутника.
S = 33 * r 2 . Цю формулу теж легко отримати з тієї, яка дана для довільного трикутника. В ній радіус множиться на суму сторін і ділиться на 4. Оскільки сторони мають однакову значення, що сума заміниться на 3а. Тепер потрібно прибрати «а», щоб залишилося тільки значення радіуса. Для цього потрібно вираз, в якому сторона ділиться на добуток 2 і синуса противолежащего стороні кута. Так як кут дорівнює 60°, то значення синуса буде 3/2. Тоді сторона виразиться через радіус так: а = 3R. Після нескладного перетворення можна прийти до того виразу для площі, яке дано спочатку.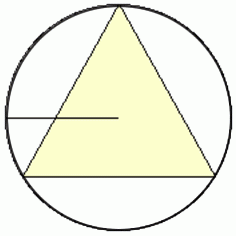 Тому формулу можна не запам'ятовувати. Тільки тримати в пам'яті співвідношення радіусів вписаного й описаного близько рівностороннього трикутника кіл.
Тому формулу можна не запам'ятовувати. Тільки тримати в пам'яті співвідношення радіусів вписаного й описаного близько рівностороннього трикутника кіл. 
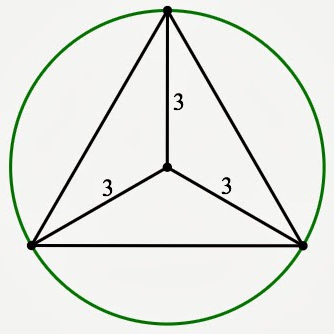
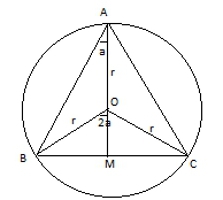

Формула 1: відома сторона
У цій та наступних формулах прийняті стандартні позначення величин трикутника. Докладніше можна подивитися у запропонованій таблиці.Величина
Її позначення
сторона
а
площа
S
висота
н
радіуси кіл вписаної та описаної
r і R, відповідно
Розрахунок площі трикутника в цьому випадку буде здійснюватися за формулою: S = 3/4 * а 2 . Вона легко виходить з тієї, яка відома для довільної фігури з трьома сторонами. Просто у формулі потрібно врахувати те, що всі сторони трикутника рівні. Якщо говорити більш точно, то потрібно формула Герона: S = (p(p-a)(p-b)(p-c)). Значення полупериметра для рівностороннього трикутника буде одно 3а/2. Таким чином, в кожній дужці під коренем вийде вираз(3а/2) - а). Воно дасть після перетворення а/2.
Так як дужок три, то у цього виразу з'явиться третя ступінь. А значить, воно перетвориться в а 3 /8. Його ще потрібно помножити на півпериметр, який визначається як сума сторін, розділена на 2. Вийде вираз: 3а 4 /16. Після вилучення квадратного кореня як раз і залишиться той вираз, що дано у першій формулі для площі рівностороннього трикутника.

Формула 2: дан радіус вписаного кола
Цей вислів дуже нагадує попередній запис. Але все ж є суттєві відмінності: використовується інша буква, ірраціональність пішла в знаменник, з'явився множник 3 і зникла цифра 4. Загалом, її легко запам'ятати.S = 33 * r 2 . Цю формулу теж легко отримати з тієї, яка дана для довільного трикутника. В ній радіус множиться на суму сторін і ділиться на 4. Оскільки сторони мають однакову значення, що сума заміниться на 3а. Тепер потрібно прибрати «а», щоб залишилося тільки значення радіуса. Для цього потрібно вираз, в якому сторона ділиться на добуток 2 і синуса противолежащего стороні кута. Так як кут дорівнює 60°, то значення синуса буде 3/2. Тоді сторона виразиться через радіус так: а = 3R. Після нескладного перетворення можна прийти до того виразу для площі, яке дано спочатку.
Формула 3: дана описана окружність і її радіус
Вона дуже схожа на першу. Тільки у її чисельнику з'являється цифра 3 і змінилася буква на R. S = 33/4 * R 2 . Оскільки радіус в два рази більше того, що розглядалося в попередньому пункті, то зрозуміло, як вона виходить. В ній просто замість r ставиться R/2. І проводяться необхідні перетворення.
Формула 4: відома висота
У цьому випадку площа рівностороннього трикутника дорівнює: S = н 2 /3. Щоб зрозуміти, як виходить така формула, потрібно знову скористатися спільною для всіх трикутників. Вона виглядає як добуток сторони на висоту і на 1/2 . Тепер, щоб дізнатися площу рівностороннього трикутника, доведеться згадати або вивести математичний вираз для висоти. Її нескладно дізнатися, якщо скористатися тим фактом, що висота утворює прямокутний трикутник. Значить, висота може бути знайдена як катет - теореми Піфагора. Другий катет дорівнює половині сторони, так як висота є ще і медіаною (це відоме властивість рівностороннього трикутника). Тоді висота буде визначатися як квадратний корінь із різниці двох квадратів. Перший «а», а другий «а/2». Після зведення у другу ступінь і добування кореня залишається: н = (3/2)*а. З нього а = 2н/3. Після підстановки його в основну для всіх трикутників формулу вийде той вираз, який зазначено на початку розділу.Приклад №1
Умова. Обчислити площу рівностороннього трикутника, якщо відомо, що його сторона має значення 4 см. Рішення. Оскільки відомо значення сторін фігури, то необхідно користуватися першою формулою. Спочатку потрібно звести в квадрат число 4. Від цього дії вийде число 16. Тепер воно скорочується з четвіркою, що стоїть в знаменнику. І в результаті в чисельнику залишається 4 і 3 а знаменник стає рівним одиниці, значить, його можна просто не записувати. Це результат, який і потрібно знайти в задачі. Відповідь: 43 см 2 .
Приклад №2
Умова. Всі сторони рівностороннього трикутника дорівнюють 22 дм. Обчислити його площу. Рішення. Міркування такі ж, як у першій задачі. Тільки значення сторони квадрата буде іншим. У ньому потрібно окремо звести у другий ступінь 2 і ірраціональність. І результат буде таким: 4*2 = 8. Після скорочення зі знаменником залишається 2 3 в чисельнику дробу, а знаменник зникає. Відповідь: 23 дм 2 .Приклад №3
Умова. В рівносторонній трикутник вписано окружність, її радіус 25 см. Необхідно обчислити площу трикутника. Рішення. Для розрахунку шуканої величини буде потрібно скористатися другою формулою. Спочатку значення радіуса потрібно звести в квадрат. Вийде 625. Потім це значення необхідно помножити на 3. Результатом цього стане число 1875. Але це ще не кінцеве значення: в ньому буде множник 3 який присутній у формулі. Відповідь: 18753 см 2 .
Приклад №4
Умова. Потрібно визначити, чому дорівнює площа рівностороннього трикутника, якщо відома його висота — 3 дм. Рішення. Природно, що потрібно вибрати четверту формулу. З її допомогою найпростіше знайти відповідь цієї задачі. Достатньо лише піднести до квадрату число 3 тобто висоту, що дасть значення 9. А потім розділити його на 3 що стоїть в формулі. Оскільки в математиці не прийнято залишати ірраціональність в знаменнику відповіді, то від нього потрібно позбутися. Для цього дріб 9/3 потрібно помножити на дріб з однаковими чисельником і знаменником, а саме 3/3. Від цього дії в чисельнику з'явиться значення 93 а в знаменнику з'явиться число 3. Цю дріб можна і потрібно скоротити на 3. Це кінцевий результат. Відповідь: площа — 33 дм 2 .
Приклад №5
Умова. Дано рівносторонній трикутник, площа якого дорівнює 27 см 2 . По цій величині потрібно дізнатися довжину сторони фігури. Рішення. Оскільки мова йде про стороні, то підійде перша формула. З неї можна одразу вивести математичне вираз, який дозволить визначити сторону трикутника. Для цього площу потрібно помножити на 4 і розділити на квадратний корінь з трьох. Так вийде значення для сторони в квадраті. Щоб отримати просто сторону, потрібно витягти корінь. Вираз для сторони буде виглядати так: а = 2 * (S/3). Так як площа відома, то можна відразу приступати до обчислень. Підкореневий вираз виглядає як приватне 27 і 3. Потрібно позбавитися від ірраціональності в знаменнику. Вийде 273 розділене на 3. Після скорочення в знаменнику залишається 1 яку можна не писати, а в чисельнику залишається 93. Наступною дією буде витяг кореня з отриманого виразу. Перший множник дає значення 3. А ось другий - 3 - вимагає до себе уваги. Щоб спростити завдання, можна витягти ці корені і округлити значення. 3 = 173; тепер з нього ще раз витягаємо корінь і отримуємо 132. Залишилося тільки помножити його на 2 і отримати шуканий результат. Відповідь: сторона дорівнює 264 см.Схожі добрі поради по темі
Як обчислити площу піраміди: підстави, бічну і повну?
При підготовці до ЄДІ з математики учням доводиться систематизувати знання з алгебри та геометрії. Хочеться об'єднати всі відомості, наприклад, про
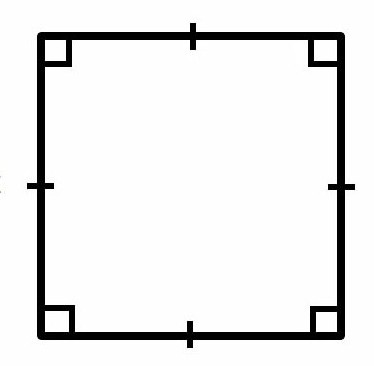
Завдання про площу квадрата і багато іншого
Такий дивовижний і знайомий квадрат. Він симетричний відносно свого центру і осей, проведених по діагоналях і через центри сторін. А шукати площа
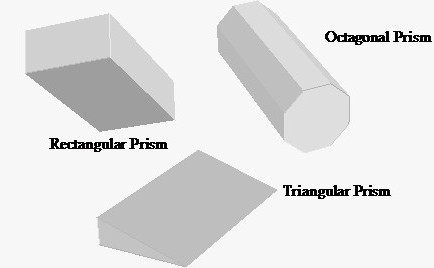
Площа підстави призми: від трикутної до багатокутної
Різні призми несхожі один на одного. У той же час у них багато спільного. Щоб знайти площу основи призми, потрібно розібратися в тому, який вигляд
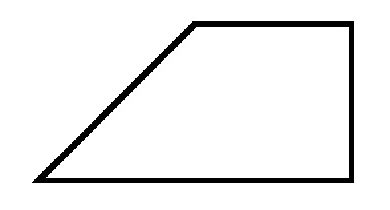
Прямокутна трапеція: всі формули та приклади завдань
Завдання з трапецією не здаються складними в ряді фігур, які вивчені раніше. Як окремий випадок розглядається прямокутна трапеція. А при пошуку її

Види трикутників. Кути трикутника
Найпростіший багатокутник, який вивчається в школі — це трикутник. Він більш зрозумілий для учнів і зустрічає менше труднощів. Незважаючи на те, що
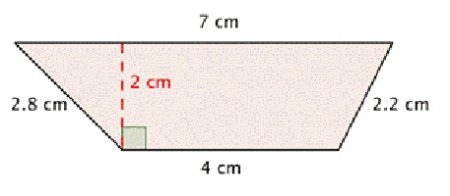
Як знайти висоту трапеції: формули на всі випадки життя
На просте питання «Як знайти висоту трапеції?» існує декілька відповідей, і все тому, що можуть бути надані різні вихідні величини. Тому і формули
