Як обчислити площу піраміди: підстави, бічну і повну?
При підготовці до ЄДІ з математики учням доводиться систематизувати знання з алгебри та геометрії. Хочеться об'єднати всі відомі відомості, наприклад, про те, як обчислити площу піраміди. Причому починаючи від заснування і бічних граней до площі всієї поверхні. Якщо з бічними гранями ситуація зрозуміла, так як вони є трикутниками, то основа завжди різне.
Правильний трикутник Тобто рівносторонній. Той, у якого всі сторони рівні і позначені літерою «а». У цьому випадку площа основи піраміди обчислюється за формулою: S = (а 2 * ?3) /4. Квадрат Формула для обчислення його площі найпростіша, тут «а» - знову сторона: S = а 2 . Довільний правильний n-кутник У сторони багатокутника те ж позначення. Для кількості кутів використовується латинська літера n. S = (n * а 2 ) /(4 * tg (180 ° /n)).
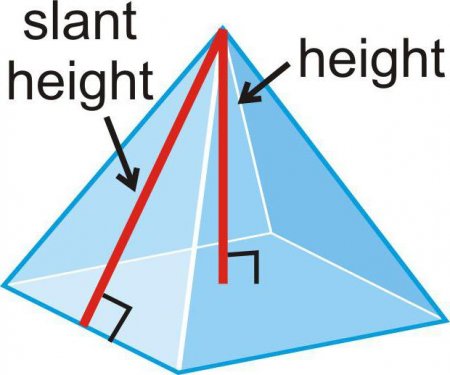
Площа рівнобедреного трикутника обчислюється за формулою, в якій половина твору підстави множиться на висоту. Ця висота в піраміді називається апофемой. Її позначення - «А». Загальна формула для площі бічної поверхні виглядає так: S = 1/2 Р*А, де Р — периметр основи піраміди. Бувають ситуації, коли не відомі сторони підстави, але дані бічні ребра (в) і плоский кут при вершині (?). Тоді покладається використовувати таку формулу, щоб обчислити бічну площа піраміди: S = n/2 * 2 sin ? .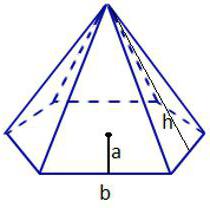
Перші розрахунки прості і призводять до такого числа: 49 мм 2 . Для другого значення потрібно обчислити півпериметр: (7 + 16*2):2 = 195 мм. Тепер можна обчислювати площу рівнобедреного трикутника: ?(195*(195-7)*(195-16) 2 ) = ?29859375 = 54644 мм 2 . Таких трикутників всього чотири, тому при підрахунку підсумкового числа його потрібно помножити на 4. Виходить: 49 + 4*54644 = 267576 мм 2 . Відповідь . Шукане значення 267576 мм 2 .
Як бути при знаходженні площі підстави піраміди?
Воно може бути абсолютно будь фігурою: від довільного трикутника до n-кутника. І це підстава, крім відмінності в кількості кутів, може бути правильною фігурою або неправильною. В цікавлять школярів завданнях з ЄДІ зустрічаються тільки завдання з правильними фігурами в підставі. Тому мова буде йти тільки про них.Правильний трикутник Тобто рівносторонній. Той, у якого всі сторони рівні і позначені літерою «а». У цьому випадку площа основи піраміди обчислюється за формулою: S = (а 2 * ?3) /4. Квадрат Формула для обчислення його площі найпростіша, тут «а» - знову сторона: S = а 2 . Довільний правильний n-кутник У сторони багатокутника те ж позначення. Для кількості кутів використовується латинська літера n. S = (n * а 2 ) /(4 * tg (180 ° /n)).
Як вступити до обчислення площі бічної та повної поверхні?
Оскільки в основі лежить правильна фігура, то всі грані піраміди виявляються рівними. Причому кожна з них є рівнобедреним трикутником, оскільки бічні ребра рівні. Тоді для того, щоб обчислити бічну площа піраміди, потрібно формула, що складається з суми однакових одночленов. Число доданків визначається кількістю сторін підстави.Площа рівнобедреного трикутника обчислюється за формулою, в якій половина твору підстави множиться на висоту. Ця висота в піраміді називається апофемой. Її позначення - «А». Загальна формула для площі бічної поверхні виглядає так: S = 1/2 Р*А, де Р — периметр основи піраміди. Бувають ситуації, коли не відомі сторони підстави, але дані бічні ребра (в) і плоский кут при вершині (?). Тоді покладається використовувати таку формулу, щоб обчислити бічну площа піраміди: S = n/2 * 2 sin ? .

Завдання № 1
Умова. Знайти загальну площу піраміди, якщо в його основі лежить рівносторонній трикутник зі стороною 4 см, а апофема має значення ?3 см. Рішення. Його починати потрібно з розрахунку периметра підстави. Оскільки це правильний трикутник, то Р = 3*4 = 12 см. Оскільки апофема відома, то можна відразу вирахувати площу всій бічній поверхні: 1/2 *12*?3 = 6?3 см 2 . Для трикутника в основі вийде таке значення площі: (4 2 *?3) /4 = 4?3 см 2 . Для визначення усієї площі буде потрібно скласти два одержані значення: 6?3 + 4?3 = 10?3 см 2 . Відповідь. 10?3 см 2 .Завдання № 2
Умова . Є правильна чотирикутна піраміда. Довжина сторони підстави дорівнює 7 мм, бічне ребро — 16 мм. Необхідно дізнатися площа її поверхні. Рішення. Оскільки багатогранник — чотирикутний і правильний, то в його основі лежить квадрат. Дізнавшись площі основи і бічних граней, вдасться порахувати площа піраміди. Формула для квадрата дана вище. А в бічних граней відомі всі сторони трикутника. Тому можна використати формулу Герона для обчислення їх площ.Перші розрахунки прості і призводять до такого числа: 49 мм 2 . Для другого значення потрібно обчислити півпериметр: (7 + 16*2):2 = 195 мм. Тепер можна обчислювати площу рівнобедреного трикутника: ?(195*(195-7)*(195-16) 2 ) = ?29859375 = 54644 мм 2 . Таких трикутників всього чотири, тому при підрахунку підсумкового числа його потрібно помножити на 4. Виходить: 49 + 4*54644 = 267576 мм 2 . Відповідь . Шукане значення 267576 мм 2 .
Завдання № 3
Умова . У правильної чотирикутної піраміди необхідно обчислити площу. В ній відома сторона квадрата — 6 см і висота — 4 см. Рішення. Найпростіше скористатися формулою з твором периметра і апофемы. Перше значення знайти просто. Друге трохи складніше. Доведеться згадати теорему Піфагора і розглянути прямокутний трикутник. Він утворений висотою піраміди і апофемой, яка є гіпотенузою. Другий катет дорівнює половині сторони квадрата, оскільки висота багатогранника падає в його середину. Шукана апофема (гіпотенуза прямокутного трикутника дорівнює ?(3 2 + 4 2 ) = 5 (см). Тепер можна обчислити шукану величину: 1/2 *(4*6)*5+6 2 = 96 (см 2 ). Відповідь. 96 см 2 .Завдання № 4
Умова. Дана правильна шестикутна піраміда. Сторони її основи дорівнюють 22 мм, бічні ребра — 61 мм. Чому дорівнює площа бічної поверхні цього многогранника? Рішення. Міркування в неї такі ж, як були описані в задачі №2. Тільки там була дана піраміда з квадратом в основі, а тепер це шестикутник. Першим ділом обчислюється площа підстави за вказаною вище формулою: (6*22 2 ) /(4*tg (180 ° /6)) = 726/(tg30?) = 726?3 см 2 . Тепер необхідно дізнатися півпериметр рівнобедреного трикутника, який є бічною гранню. (22+61*2):2 = 72 см. Залишилося за формулою Герона порахувати площа кожного такого трикутника, а потім помножити її на шість і скласти з тієї, що вийшла для підстави. Розрахунки за формулою Герона: ?(72*(72-22)*(72-61) 2 )=?435600=660 см 2 . Обчислення, які дадуть площа бічної поверхні: 660*6 = 3960 см 2 . Залишилося їх скласти, щоб дізнатися всю поверхню: 521747?5217 см 2 . Відповідь. Підстави - 726?3 см 2 , бічній поверхні - 3960 см 2 уся площа - 5217 см 2 .Схожі добрі поради по темі
Площа підстави призми: від трикутної до багатокутної
Різні призми несхожі один на одного. У той же час у них багато спільного. Щоб знайти площу основи призми, потрібно розібратися в тому, який вигляд
Прямокутна трапеція: всі формули та приклади завдань
Завдання з трапецією не здаються складними в ряді фігур, які вивчені раніше. Як окремий випадок розглядається прямокутна трапеція. А при пошуку її
Приклади того, як обчислити площу циліндра
Існує велика кількість задач, пов'язаних з циліндром. У них потрібно знаходити радіус і висоту тіла або його вигляд перерізу. Плюс до всього, іноді
Всі тонкощі того, як обчислити площу паралелепіпеда
Паралелепіпед - найпоширеніша фігура з тих, що оточують людей. Більшість приміщень являють собою саме його. Особливо важливо знати площа
Всі варіанти того, як знайти площу трапеції
Багатолика трапеція Вона може бути довільною, равнобедренной або прямокутної. І в кожному випадку потрібно знати, як знайти площу трапеції. Звичайно,
Як дізнатися площу рівностороннього трикутника: основні формули
Знайти площу рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована