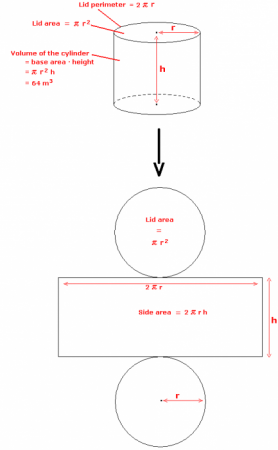
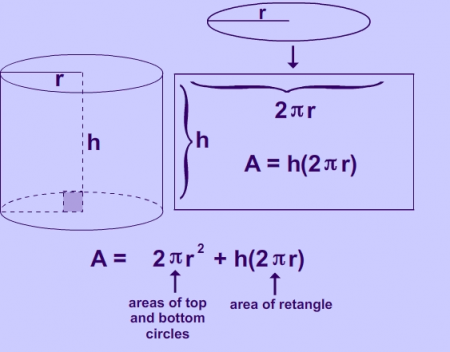
Приклади того, як обчислити площу циліндра
Існує велика кількість задач, пов'язаних з циліндром. У них потрібно знаходити радіус і висоту тіла або його вигляд перерізу. Плюс до всього, іноді потрібно обчислити площу циліндра і його обсяг. 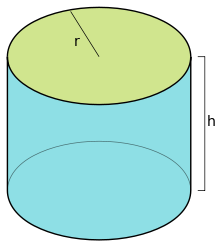
Підстав у два циліндра. Вони дорівнюють один одному і з'єднані відрізками, які сполучають відповідні точки підстав. Вони називаються утворюють циліндра. Всі твірні паралельні один одному і рівні. Саме вони складають бічну поверхню тіла.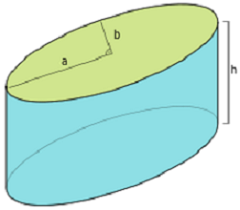 У загальному випадку циліндр — це похиле тіло. Якщо утворюють складають прямий кут з підставами, то говорять вже про прямий фігурі. Цікаво, що круговий циліндр є тілом обертання. Він виходить від повороту прямокутника навколо однієї з його сторін.
У загальному випадку циліндр — це похиле тіло. Якщо утворюють складають прямий кут з підставами, то говорять вже про прямий фігурі. Цікаво, що круговий циліндр є тілом обертання. Він виходить від повороту прямокутника навколо однієї з його сторін. Висота. Вона є найкоротшим відстанню між основами циліндра. Якщо він прямий, то висота збігається з твірною. Радіус. Збігається з тим, який можна провести в підставі. Вісь. Це пряма лінія, яка містить центри обох підстав. Вісь завжди паралельна всім утворюючим. У прямому циліндрі вона перпендикулярна підстав. Осьовий переріз. Воно утворюється при перетині циліндра площиною, що містить вісь. Дотична площина. Вона проходить через одну з утворюючих і перпендикулярна осьового перерізу, яке проведено через цю твірну. 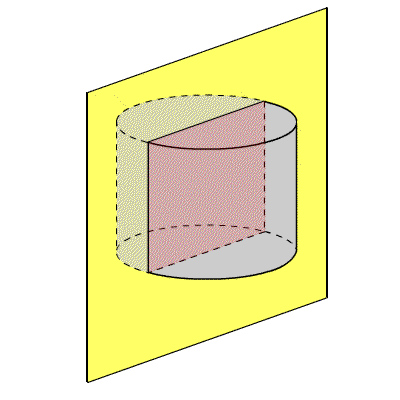
S пліч = l * н, де н — твірна, l — довжина кола. Причому останній параметр обчислюється за формулою: l = 2 * r, тут r — радіус кола, - число "пі", що дорівнює 314. Оскільки підстава - коло, то його площа обчислюється за допомогою такого виразу: S осн = * r 2 .

Яке тіло є циліндром?
У курсі шкільної програми вивчається кругової, тобто є таким підставі, циліндр. Але виділяють ще і еліптичний вигляд даної фігури. З назви ясно, що його підставою буде еліпс або овал.Підстав у два циліндра. Вони дорівнюють один одному і з'єднані відрізками, які сполучають відповідні точки підстав. Вони називаються утворюють циліндра. Всі твірні паралельні один одному і рівні. Саме вони складають бічну поверхню тіла.

Основні елементи циліндра
Основні елементи циліндра виглядають наступним чином.
Як пов'язаний циліндр з вписаною в нього або описаної біля нього призмою?
Іноді зустрічаються задачі, в яких потрібно обчислити площу циліндра, а відомі при цьому деякі елементи пов'язаної з ним призми. Як співвідносяться ці фігури? Якщо призма вписана в циліндр, то її заснування – рівні многокутники. Причому вони вписані у відповідні підстави циліндра. Бічні ребра призми збігаються з утворюючими. У описаної призми в підставах перебувають правильні багатокутники. Вони описані близько кіл циліндра, які є підставами. Площини, які містять грані призми, стосуються циліндра по твірним.Про площі бічної поверхні і основи для прямого кругового циліндра
Якщо зробити розгортку бічної поверхні, то вийде прямокутник. Його сторони будуть збігатися з твірною і довжиною окружності підстави. Тому бокова площа циліндра дорівнює добутку цих двох величин. Якщо записати формулу, то вийде наступне:S пліч = l * н, де н — твірна, l — довжина кола. Причому останній параметр обчислюється за формулою: l = 2 * r, тут r — радіус кола, - число "пі", що дорівнює 314. Оскільки підстава - коло, то його площа обчислюється за допомогою такого виразу: S осн = * r 2 .

Про площі всієї поверхні прямого кругового циліндра
Так як вона утворена двома підставами і бічною поверхнею, то потрібно скласти ці три величини. Тобто повна площа циліндра буде обчислюватись за формулою: S підлогу = 2 * r * n + 2 * r 2 . Часто її записують в іншому вигляді: S підлогу = 2 * r (н + r).Про площах похилого кругового циліндра
Що стосується підстав, то там всі формули ті ж, адже вони як і раніше кола. А ось бічна поверхня вже не дає прямокутника. Для розрахунку площі бічної поверхні похилого циліндра потрібно перемножити значення твірної та периметра перерізу, яке буде перпендикулярно обраної утворюючої. Формула виглядає так: S пліч = х * Р, де х — довжина твірної циліндра, Р — периметр перерізу. Переріз, до речі, краще вибирати таке, щоб воно утворювало еліпс. Тоді будуть спрощені розрахунки його периметра. Довжина еліпса обчислюється за формулою, яка дає приблизний відповідь. Але його часто буває достатньо для завдань шкільного курсу: l = * (а + в), де «а» і «в» — півосі еліпса, тобто відстані від центру до найближчої і найдальшої його точок. Площа всієї поверхні потрібно обчислювати за допомогою такого виразу: S підлогу = 2 * r 2 + х * Р.Чому дорівнюють деякі перерізу прямого кругового циліндра?
Коли переріз проходить через вісь, то його площа визначається як добуток утворює і діаметра підстави. Це пояснюється тим, що воно має вигляд прямокутника, сторони якого збігаються з позначеними елементами. Щоб знайти площу перерізу циліндра, що є паралельним осьовому, потрібно теж формула для прямокутника. У цій ситуації одна його сторона, як і раніше буде збігатися з висотою, а інша дорівнює хорді підстави. Остання ж збігається з лінією перетину з основи. Коли перетин перпендикулярно осі, то вона має вигляд кола. Причому його площа така ж, як у підстави фігури. Можливо ще перетин під деяким кутом до осі. Тоді в перерізі виходить овал або його частина.Приклади завдань
Завдання №1. Дан прямий циліндр, площа підстави якого 1256 см 2 . Необхідно обчислити повну площа циліндра, якщо його висота дорівнює 3 см. Рішення. Необхідно скористатися формулою для повної площі прямого кругового циліндра. Але в ній не вистачає даних, а саме радіусу основи. Зате відома площа кола. З неї легко обчислити радіус. Він виявляється рівним квадратному кореню з приватного, яке виходить від ділення площі підстави на пі. Після поділу 1256 на 314 виходить 4. Квадратний корінь з 4 — це 2. Тому радіус буде мати саме таке значення. Тепер можна підрахувати площу бічної поверхні. Для цього слід помножити пі на дальність, висоту і 2. Твір буде виглядати так: 314 * 3 * 2 * 2. Підсумком дій є: 3768 см 2 . Для того щоб порахувати повну площу потрібно скласти два підстави (1256 см 2 ) і бічну поверхню (3768 см 2 ). У результаті виходить число 5024 см 2 . Відповідь: S підлогу = 5024 см 2 . Завдання №2. Циліндр з радіусом 5 см припинений площиною, паралельною осі. Відстань від перерізу до осі дорівнює 3 см. Висота циліндра — 4 см. Потрібно знайти площу перерізу. Рішення. Форма перерізу — прямокутна. Одна його сторона збігається з висотою циліндра, а інша дорівнює хорде. Якщо перша величина відома, то другу потрібно знайти. Для цього слід зробити додаткове побудова. На підставі проводимо два відрізки. Обидва вони будуть починатися в центрі кола. Перша буде закінчуватися в центрі хорди і дорівнювати відомому відстані до осі. Друга — на кінці хорди. Вийде прямокутний трикутник. У ньому відомі гіпотенуза і один з катетів. Гіпотенуза збігається з радіусом. Другий катет дорівнює половині хорди. Невідомий катет, помножений на 2 дасть шукану довжину хорди. Обчислимо його значення. Для того щоб знайти невідомий катет, потрібно звести в квадрат гіпотенузи і відомий катет, відняти від першого друге і витягти квадратний корінь. Квадрати рівні 25 і 9. Їх різниця – 16. Після витягання квадратного кореня залишається 4. Це шуканий катет. Хорда буде дорівнює 4 * 2 = 8 (см). Тепер можна обчислити площу перетину: 8 * 4 = 32 (см 2 ). Відповідь: S січ дорівнює 32 см 2 . Завдання №3. Необхідно обчислити площу осьового перерізу циліндра. Відомо, що в нього вписаний куб з ребром 10 см. Рішення. Осьовий переріз циліндра співпадає з прямокутником, який проходить через чотири вершини куба і містить діагоналі його підстав. Сторона куба є твірною циліндра, а діагональ підстави збігається з діаметром. Добуток цих двох величин дасть площа, яку треба дізнатися в задачі. Для пошуку діаметра потрібно скористатися знанням того, що в основі куба – квадрат, а його діагональ утворює прямокутний трикутник рівносторонній. Гіпотенуза його є шуканої діагоналлю фігури. Для її розрахунку потрібно формула теореми Піфагора. Потрібно звести в квадрат сторону куба, помножити її на 2 і витягти квадратний корінь. Десять по другій ступені — це сто. Помножене на 2 — двісті. Квадратний корінь з 200 дорівнює 102. Переріз – це знову прямокутник зі сторонами 10 і 102. Його площа легко порахувати, перемноживши ці значення. Відповідь. S січ = 1002 см 2 .Схожі добрі поради по темі

Двигун зовнішнього згорання: види, принцип роботи, особливості
В даний час всім відомо, що людством використовуються двигуни внутрішнього згоряння. Однак так було не завжди. Перші зразки таких пристроїв були
Площа підстави призми: від трикутної до багатокутної
Різні призми несхожі один на одного. У той же час у них багато спільного. Щоб знайти площу основи призми, потрібно розібратися в тому, який вигляд
Прямокутна трапеція: всі формули та приклади завдань
Завдання з трапецією не здаються складними в ряді фігур, які вивчені раніше. Як окремий випадок розглядається прямокутна трапеція. А при пошуку її
Всі варіанти того, як знайти площу трапеції
Багатолика трапеція Вона може бути довільною, равнобедренной або прямокутної. І в кожному випадку потрібно знати, як знайти площу трапеції. Звичайно,
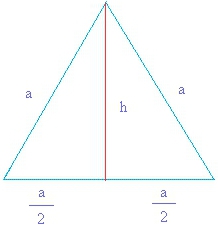
Як дізнатися площу рівностороннього трикутника: основні формули
Знайти площу рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована

Як зробити циліндр своїми руками: керівництво по експлуатації
Колись, ще на початку минулого століття циліндр був невід'ємною частиною туалету всіх справжніх джентльменів. Зараз цей предмет гардероба пішов