Всі варіанти того, як знайти площу трапеції
Багатолика трапеція Вона може бути довільною, равнобедренной або прямокутної. І в кожному випадку потрібно знати, як знайти площу трапеції. Звичайно, простіше всього запам'ятати основні формули. Але іноді простіше скористатися тією, яка виведена з урахуванням всіх особливостей конкретної геометричної фігури.
висота, тобто відрізок, перпендикулярний обом підстав; середня лінія, яка має своїми кінцями середини бічних сторін.
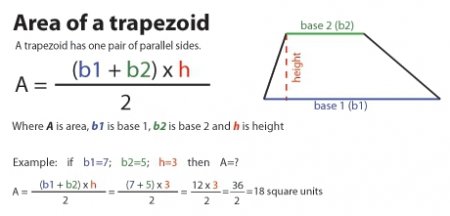
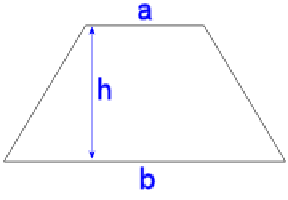 Якщо позначити підстави літерами а 1 і а 2 , висоту — н, то формула для площі буде виглядати так: S = ((а 1 + а 2 )/2)*н.
Якщо позначити підстави літерами а 1 і а 2 , висоту — н, то формула для площі буде виглядати так: S = ((а 1 + а 2 )/2)*н.
S = ((д 1 * д 2 )/2) * sin . В цьому виразі можна легко замінити на . Результат не зміниться.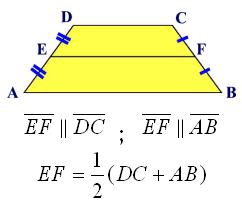
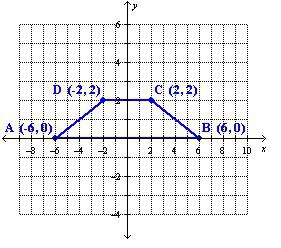
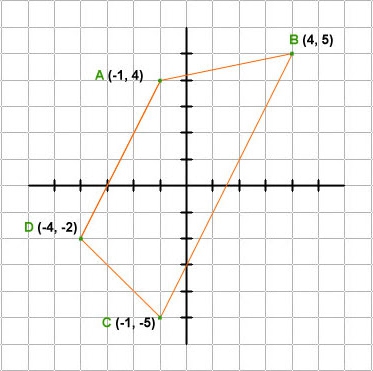 № 3. Умова. Елементи равнобедренной трапеції мають такі значення: нижня основа - 14 см, верхнє — 4 см, гострий кут — 45o. Потрібно обчислити її площу. Рішення. Нехай менше підставу має позначення ЗС. Висота, проведена з точки В, буде називатися ВН. Оскільки кут 45o, то трикутник АВН вийде і прямокутний рівнобедрений. Значить, АН=ВН. Причому АН дуже легко знайти. Вона дорівнює половині різниці підстав. Тобто(14 - 4) /2 = 10 /2 = 5 (см). Підстави відомі, висота злічено. Можна користуватися першою формулою, яка тут була розглянута для довільної трапеції. S= ((14 + 4) /2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2 ). Відповідь: Шукана площа дорівнює 45 см 2 . № 4. Умова. Є довільна трапеція АВСД. На її бічних сторонах взяті точки О і Е, так що Е паралельна підставі АТ. Площа трапеції АОЕД в п'ять разів більше, ніж у ВІВСІ. Обчислити значення Е, якщо відомі довжини підстав. Рішення. Потрібно провести дві паралельні прямі АВ: першу через точку С, її перетин з Е — точка Т; другу через Е і точкою перетину з АД буде М. Нехай невідома Е=х. Висота меншою трапеції ВІВСІ — н 1 , більшою АОЕД — н 2 . Оскільки площі цих двох трапецій співвідносяться як 1 до 5 то можна записати таке рівняння: (х + а 2 ) * н 1 = 1/5 (х + а 1 ) * н 2 або н 1 /н 2 = (х + а 1 ) /(5(х + а 2 )). Висоти і сторони трикутників пропорційні побудови. Тому можна записати ще одне рівність: н 1 /н 2 = (х - а 2 ) /(а 1 - х). У двох останніх записах в лівій частині стоять рівні величини, значить, можна написати, що (х + а 1 ) /(5(х + а 2 )) дорівнює (х - а 2 ) /(а 1 - х). Тут потрібно провести ряд перетворень. Спочатку перемножити хрест навхрест. З'являться дужки, які вкажуть на різницю квадратів, після застосування цієї формули вийде короткий рівняння. У ньому потрібно розкрити дужки і перенести всі доданки з невідомої «х» в ліву сторону, а потім витягти квадратний корінь. Відповідь : х = {(а 1 2 + 5 а 2 2 ) /6}.
№ 3. Умова. Елементи равнобедренной трапеції мають такі значення: нижня основа - 14 см, верхнє — 4 см, гострий кут — 45o. Потрібно обчислити її площу. Рішення. Нехай менше підставу має позначення ЗС. Висота, проведена з точки В, буде називатися ВН. Оскільки кут 45o, то трикутник АВН вийде і прямокутний рівнобедрений. Значить, АН=ВН. Причому АН дуже легко знайти. Вона дорівнює половині різниці підстав. Тобто(14 - 4) /2 = 10 /2 = 5 (см). Підстави відомі, висота злічено. Можна користуватися першою формулою, яка тут була розглянута для довільної трапеції. S= ((14 + 4) /2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2 ). Відповідь: Шукана площа дорівнює 45 см 2 . № 4. Умова. Є довільна трапеція АВСД. На її бічних сторонах взяті точки О і Е, так що Е паралельна підставі АТ. Площа трапеції АОЕД в п'ять разів більше, ніж у ВІВСІ. Обчислити значення Е, якщо відомі довжини підстав. Рішення. Потрібно провести дві паралельні прямі АВ: першу через точку С, її перетин з Е — точка Т; другу через Е і точкою перетину з АД буде М. Нехай невідома Е=х. Висота меншою трапеції ВІВСІ — н 1 , більшою АОЕД — н 2 . Оскільки площі цих двох трапецій співвідносяться як 1 до 5 то можна записати таке рівняння: (х + а 2 ) * н 1 = 1/5 (х + а 1 ) * н 2 або н 1 /н 2 = (х + а 1 ) /(5(х + а 2 )). Висоти і сторони трикутників пропорційні побудови. Тому можна записати ще одне рівність: н 1 /н 2 = (х - а 2 ) /(а 1 - х). У двох останніх записах в лівій частині стоять рівні величини, значить, можна написати, що (х + а 1 ) /(5(х + а 2 )) дорівнює (х - а 2 ) /(а 1 - х). Тут потрібно провести ряд перетворень. Спочатку перемножити хрест навхрест. З'являться дужки, які вкажуть на різницю квадратів, після застосування цієї формули вийде короткий рівняння. У ньому потрібно розкрити дужки і перенести всі доданки з невідомої «х» в ліву сторону, а потім витягти квадратний корінь. Відповідь : х = {(а 1 2 + 5 а 2 2 ) /6}.
Кілька слів про трапеції та її елементах
Будь-чотирикутник, у якого дві сторони паралельні, можна назвати трапецією. У загальному випадку вони не рівні і називаються підставами. Більша з них — нижня, а інше — верхнє. Дві інші сторони виявляються бічними. У довільній трапеції вони мають різну довжину. Якщо ж вони рівні, то фігура стає равнобедренной. Якщо раптом кут між будь бічною стороною і підставою виявиться рівним 90 градусів, то трапеція є прямокутною. Всі ці особливості можуть допомогти у вирішенні задачі про те, як знайти площу трапеції. Серед елементів фігури, які можуть виявитися незамінними у вирішенні завдань, можна виділити такі:За якою формулою обчислити площу, якщо відомі підстави і висота?
Це вираз дається основним, тому що найчастіше можна дізнатися ці величини, навіть коли вони не надані явно. Отже, щоб зрозуміти, як знайти площу трапеції, потрібно скласти обидва підстави і розділити їх на два. Отримане значення потім ще помножити на значення висоти.
Формула, за якою обчислюється площа, якщо дано її висота і середня лінія
Якщо подивитися уважно на попередню формулу, то легко помітити, що в ній явно присутній значення середньої лінії. А саме, сума підстав, поділена на два. Нехай середня лінія буде позначена буквою l, тоді формула для площі стане такою: S = l * н.Можливість знайти площу по діагоналях
Цей спосіб допоможе, якщо відомий кут, утворений ними. Припустимо, що діагоналі позначені літерами д 1 і д 2 , а кути між ними — і . Тоді формула того, як знайти площу трапеції, буде записана наступним чином:S = ((д 1 * д 2 )/2) * sin . В цьому виразі можна легко замінити на . Результат не зміниться.

Як дізнатися площа, якщо відомі всі сторони фігури?
Бувають і такі ситуації, коли в цій фігурі відомі саме сторони. Ця формула виходить громіздкою і її складно запам'ятати. Але можливо. Нехай бокові сторони мають позначення: в 1 і в 2 основу а 1 більше, ніж а 2 . Тоді формула площі прийме такий вигляд: S = ((а 1 + а 2 ) /2) * {у 1 2 -[(а1 - а2)2 + в1 2 - в2 2) /(2 * (а1 - а2))] 2 }.Способи обчислення площі равнобедренной трапеції
Перший пов'язаний з тим, що в неї можна вписати коло. І, знаючи її радіус (він позначається буквою r), а також кут при основі — , можна скористатися такою формулою: S = (4 * r 2 ) /sin . Остання загальна формула, яка заснована на знанні всіх сторін фігури, істотно спрощується за рахунок того, що бічні сторони мають однакове значення: S = ((а 1 + а 2 ) /2) * {у 2 -[(а1 - а2)2 /(2 * (а1 - а2))] 2 }.Методи обчислення площі прямокутної трапеції
Зрозуміло, що підійде будь-який з перерахованих для довільної фігури. Але іноді корисно знати про особливості такої трапеції. Вона полягає в тому, що різниця квадратів довжин діагоналей дорівнює різниці, складеної з квадратів підстав. Часто формули для трапеції забуваються, у той час як вираження для площ прямокутника і трикутника пам'ятаються. Тоді можна застосувати простий спосіб. Розділити трапецію на дві фігури, якщо вона прямокутна, або три. Одна точно буде прямокутником, а друга, або дві, що залишилися, трикутниками. Після обчислення площ цих фігур залишиться їх тільки скласти. Це досить простий спосіб того, як знайти площу прямокутної трапеції.Як бути, якщо відомі координати вершин трапеції?
У цьому випадку потрібно скористатися виразом, який дозволяє визначити відстань між точками. Його можна застосувати три рази: для того, щоб дізнатися обидва підстави і одну висоту. А потім просто застосувати першу формулу, яка описана трохи вище. Для ілюстрації такого методу можна навести такий приклад. Дано вершини з координатами А(5; 7), (8; 7), (10; 1), D(1; 1). Потрібно дізнатися площа фігури. До того як знайти площу трапеції, по координатах потрібно обчислити довжини підстав. Буде потрібно така формула: довжина відрізка = {(різниця перших координат точок) 2 + (різниця друге координат точок) 2 }. Верхнє підставу позначено АВ, значить, його довжина дорівнює {(8-5) 2 + (7-7) 2 } = 9 = 3. Нижнє — СД = {(10-1) 2 + (1-1) 2 } = 81 = 9. Тепер потрібно провести висоту з вершини на основу. Нехай її початок буде в точці А. Кінець відрізка виявиться на нижньому підставі в точці з координатами (5; 1), нехай це буде точка Н. Довжина відрізка АН вийде рівною {(5-5) 2 + (7-1) 2 } = 36 = 6. Залишилося тільки підставити получавшиеся значення у формулу площі трапеції: S= ((3 + 9) /2) * 6 = 36. Задача вирішена без одиниць вимірювання, тому що не вказаний масштаб координатної сітки. Він може бути як міліметр, так і метр.
Приклади завдань
№ 1. Умова. Відомий кут між діагоналями довільній трапеції, він дорівнює 30 градусам. Менша діагональ має значення 3 дм, а друга більше її в 2 рази. Необхідно порахувати площу трапеції. Рішення. Для початку потрібно дізнатися довжину другої діагоналі, тому що без цього не вдасться порахувати відповідь. Обчислити її нескладно, 3 * 2 = 6 (дм). Тепер потрібно скористатися відповідною формулою для площі: S= ((3 * 6) /2) * sin 30o = 18/2 * 1/2 = 45 (дм 2 ). Задача вирішена. Відповідь: площа трапеції дорівнює 45 дм 2 . № 2. Умова. У трапеції АВСД підставами є відрізки АТ і ВС. Точка Е - середина сторони СД. З неї проведено перпендикуляр до прямої АВ, кінець цього відрізка позначений літерою Н. Відомо, що довжини АВ і ЕН дорівнюють відповідно 5 і 4 см. Потрібно обчислити площу трапеції. Рішення. Для початку потрібно зробити креслення. Оскільки значення перпендикуляра менше сторони, до якої він проведений, то трапеція буде трохи витягнутої вгору. Так ЄП виявиться всередині фігури. Щоб виразно побачити хід рішення завдання, потрібно виконати додаткове побудова. А саме, провести пряму, яка паралельна стороні АВ. Точки перетину цієї прямої з АД — Р, а з продовженням ВС — Г. Вийшла фігура ВХРА — паралелограм. Причому його площа дорівнює очікуваної. Це пов'язано з тим, що трикутники, які вийшли при додатковому побудові, рівні. Це випливає з рівності сторони та двох прилеглих до неї кутів, один — вертикальний, інший - навхрест лежить. Знайти площа паралелограма можна за формулою, яка містить твір боку і висоти, опущеної на неї. Таким чином, площа трапеції дорівнює 5 * 4 = 20 см 2 . Відповідь: S = 20 см 2 .
Схожі добрі поради по темі
Прямокутна трапеція: всі формули та приклади завдань
Завдання з трапецією не здаються складними в ряді фігур, які вивчені раніше. Як окремий випадок розглядається прямокутна трапеція. А при пошуку її

Лицемір – це що за людина?
Михайло Пришвін одного разу сказав: «Лицемір – це людина, що вимірює вчинки не своєю совістю, а думкою інших». А Фрейд був переконаний в тому, що

Сукні-трапеції – ідеальне рішення для будь-якого типу фігури!
Сучасні моделі жіночих суконь вражають своєю різноманітністю. Але як підібрати свій ідеальний фасон, який не тільки приховає недоліки фігури, але і
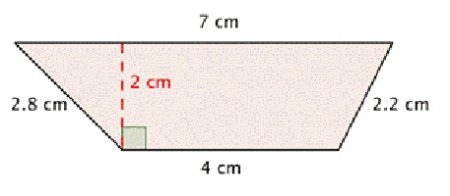
Як знайти висоту трапеції: формули на всі випадки життя
На просте питання «Як знайти висоту трапеції?» існує декілька відповідей, і все тому, що можуть бути надані різні вихідні величини. Тому і формули
Як дізнатися площу рівностороннього трикутника: основні формули
Знайти площу рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована

Масивна шия - як накачати трапецію
У деяких людей розвиток одних м'язів відбувається з неймовірною швидкістю, у той час як інші розвиваються повільно і постійно. Або ж просто вони не