Прямокутна трапеція: всі формули та приклади завдань
Завдання з трапецією не здаються складними в ряді фігур, які вивчені раніше. Як окремий випадок розглядається прямокутна трапеція. А при пошуку її площі іноді буває зручніше розбити її на дві вже знайомі: квадрат і трикутник. Варто тільки трохи подумати, і рішення обов'язково знайдеться.
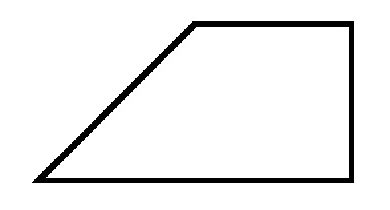
Інші кути у прямокутній трапеції - це завжди гострий і тупий. Причому їх сума завжди буде дорівнює 180 градусам. Кожна діагональ утворює з її меншою бічною стороною прямокутний трикутник. А висота, проведена з вершини з тупим кутом, ділить фігуру на дві. Одна з них прямокутник, а інша - прямокутний трикутник. До речі, ця сторона завжди дорівнює висоті трапеції.
Величина
Її позначення
a
більша підстава
b
менше підставу прямокутної трапеції
c, h
перпендикулярна до підстав бічна сторона, висота
d
похила-бічна сторона
гострий кут
тупий кут
м
середня лінія трапеції
д 1
менша діагональ
д 2
велика діагональ
з = d *sin; c = (a - b) * tg ; c = (d 2 - (a - b) 2 ). Перша випливає з прямокутного трикутника. І говорить про те, що катет до гіпотенузі дає синус противолежащего кута. У тому ж трикутнику другий катет дорівнює різниці двох підстав. Тому справедливо твердження, яке прирівнює тангенс кута до стосовно катетів. З того самого трикутника можна вивести формулу, ґрунтуючись на знанні теореми Піфагора. Це третє записане вираз.
Можна записати формули для іншої бічної сторони. Їх теж три: d = (a - b) /cos ; d = c /sin ; d = (c 2 + (а – b) 2 ). Перші дві знову виходять із співвідношення сторін у тому ж прямокутному трикутнику, а друга виводиться з теореми Піфагора.
d1 = (з 2 + b 2 ) або по-іншому, замінивши «з» на «h»: d1 = (h 2 + b 2 ). Аналогічним чином виходять формули для другої діагоналі: d2 = (з 2 + b 2 ) або d 2 = (h 2 + а 2 ).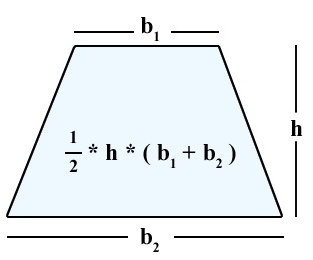
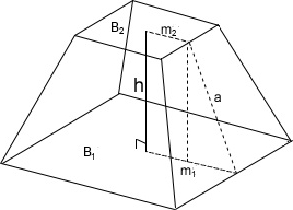
Визначення прямокутної трапеції та її властивості
У довільній трапеції підстави паралельні, а бічні сторони можуть мати довільне значення кутів до них. Якщо розглядається прямокутна трапеція, то в ній одна із сторін завжди перпендикулярна підстав. Тобто два кута в ній будуть рівні 90 градусам. Причому вони завжди належать суміжних вершин або, іншими словами, одній бічній стороні.
Інші кути у прямокутній трапеції - це завжди гострий і тупий. Причому їх сума завжди буде дорівнює 180 градусам. Кожна діагональ утворює з її меншою бічною стороною прямокутний трикутник. А висота, проведена з вершини з тупим кутом, ділить фігуру на дві. Одна з них прямокутник, а інша - прямокутний трикутник. До речі, ця сторона завжди дорівнює висоті трапеції.
Які позначення прийняті в представлених формулах?
Всі величини, що використовуються в різних виразах, що описують трапецію, зручно відразу обумовити і представити в таблиці:Величина
Її позначення
a
більша підстава
b
менше підставу прямокутної трапеції
c, h
перпендикулярна до підстав бічна сторона, висота
d
похила-бічна сторона
гострий кут
тупий кут
м
середня лінія трапеції
д 1
менша діагональ
д 2
велика діагональ
Формули, які описують елементи прямокутної трапеції
Найпростіша з них пов'язує висоту і меншу бічну сторону: c = h. Ще кілька формул для цієї сторони прямокутної трапеції:з = d *sin; c = (a - b) * tg ; c = (d 2 - (a - b) 2 ). Перша випливає з прямокутного трикутника. І говорить про те, що катет до гіпотенузі дає синус противолежащего кута. У тому ж трикутнику другий катет дорівнює різниці двох підстав. Тому справедливо твердження, яке прирівнює тангенс кута до стосовно катетів. З того самого трикутника можна вивести формулу, ґрунтуючись на знанні теореми Піфагора. Це третє записане вираз.

Можна записати формули для іншої бічної сторони. Їх теж три: d = (a - b) /cos ; d = c /sin ; d = (c 2 + (а – b) 2 ). Перші дві знову виходять із співвідношення сторін у тому ж прямокутному трикутнику, а друга виводиться з теореми Піфагора.
Якою формулою можна скористатися для розрахунку площі?
Тій, що надана для довільної трапеції. Тільки треба врахувати, що заввишки є сторона, перпендикулярна до таких підстав. S = (a + b) * h /2. Ці величини не завжди дано явно. Тому щоб обчислити площу прямокутної трапеції, потрібно виконати деякі математичні викладки.
Як бути, якщо потрібно обчислити діагоналі?
В цьому випадку потрібно побачити, що вони утворюють два прямокутних трикутника. Отже, завжди можна скористатися теоремою Піфагора. Тоді перша діагональ буде виражатися так:d1 = (з 2 + b 2 ) або по-іншому, замінивши «з» на «h»: d1 = (h 2 + b 2 ). Аналогічним чином виходять формули для другої діагоналі: d2 = (з 2 + b 2 ) або d 2 = (h 2 + а 2 ).
Завдання №1
Умова . Площа прямокутної трапеції відома і дорівнює 120 дм 2 . Її висота має довжину 8 дм. Необхідно обчислити всі сторони трапеції. Додатковою умовою є те, що одна підстава менше іншого на 6 дм. Рішення. Оскільки дана прямокутна трапеція, у якої відома висота, то одразу ж можна сказати про те, що одна із сторін дорівнює 8 дм, тобто менша бічна сторона. Тепер можна порахувати іншу: d = (з 2 + (а – b) 2 ). Причому тут відразу дані і сторона, і різниця підстав. Останнє дорівнює 6 дм, це відомо з умови. Тоді d буде дорівнювати квадратному кореню (64 + 36), тобто з 100. Так знайдена ще одна бічна сторона дорівнює 10 дм. Суму підстав можна знайти з формули для площі. Вона буде дорівнює подвоєному значенню площі, розділеному на висоту. Якщо вважати, то виходить 240 /8. Отже, сума підстав — це 30 дм. З іншого боку, їх різниця дорівнює 6 дм. Об'єднавши ці рівняння, можна порахувати обидва підстави: а + b = 30 і а - b = 6. Можна висловити а (b + 6), підставити його в перше рівність. Тоді вийде, що 2b буде дорівнювати 24. Тому просто b виявиться 12 дм. Тоді остання сторона дорівнює 18 дм. Відповідь. Сторони прямокутної трапеції: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Завдання №2
Умова. Дана прямокутна трапеція. Її більша бічна сторона дорівнює сумі підстав. Її висота має довжину 12 см. Побудований прямокутник, сторони якого дорівнюють підстав трапеції. Необхідно обчислити площу цього прямокутника. Рішення. Почати потрібно з шуканого. Потрібна площа визначиться як добуток a і b. Обидві ці величини не відомі. Потрібно використовувати додаткові рівності. Одне з них побудовано на твердженні з умови: d = а + b. Необхідно скористатися третьою формулою для цієї сторони, яка дана вище. Вийде: d 2 = з 2 + (a – b) 2 або (a + b) 2 = з 2 + (a – b) 2 . Необхідно зробити перетворення, підставивши замість його значення з умови - 12. Після розкриття дужок і зведення подібних доданків виходить, що 144 = 4 ab. На початку рішення йшлося про те, що а*b дає шукану площу. Тому в останньому виразі можна замінити це твір S. Простий розрахунок дасть значення площі. S = 36 см 2 . Відповідь. Шукана площа 36 см 2 .
Завдання №3
Умова. Площа прямокутної трапеції 1503 см2. Гострий кут дорівнює 60 градусам. Таке ж значення має кут між маленьким підставою і меншою діагоналлю. Потрібно обчислити меншу діагональ. Рішення. Властивості кутів трапеції виходить, що її тупий кут дорівнює 120o. Тоді діагональ ділить його на рівні, тому що одна його частина вже 60 градусів. Тоді і кут між діагоналлю і другою підставою теж 60 градусів. Тобто трикутник, утворений великою підставою, похилій бічною стороною і меншою діагоналлю, є рівностороннім. Таким чином, шукана діагональ дорівнює а, як і бічна сторона d = а. Тепер потрібно розглянути прямокутний трикутник. У ньому третій кут дорівнює 30 градусам. Значить катет, що лежить проти нього, дорівнює половині гіпотенузи. Тобто менша основа трапеції дорівнює половині шуканої діагоналі: b = a/2. З нього ж потрібно знайти висоту, рівну бічній стороні, перпендикулярній підстав. Сторона тут катет. З теореми Піфагора: з = (a/2) * 3. Тепер залишилося тільки підставити всі величини в формулу площі: 1503 = (a + a/2) * (a/2 * 3) /2. Рішення цього рівняння дає корінь 20 Відповідь. Менша діагональ має довжину 20 см.Схожі добрі поради по темі
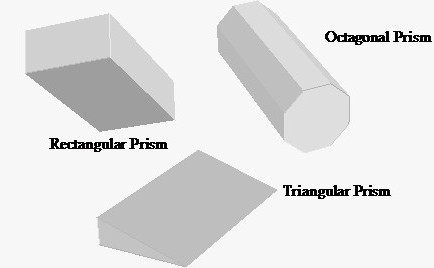
Площа підстави призми: від трикутної до багатокутної
Різні призми несхожі один на одного. У той же час у них багато спільного. Щоб знайти площу основи призми, потрібно розібратися в тому, який вигляд
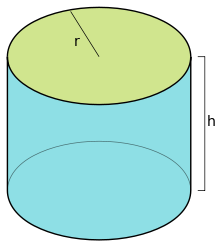
Приклади того, як обчислити площу циліндра
Існує велика кількість задач, пов'язаних з циліндром. У них потрібно знаходити радіус і висоту тіла або його вигляд перерізу. Плюс до всього, іноді
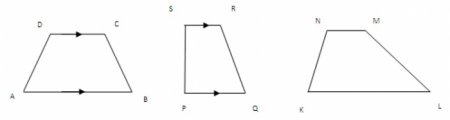
Всі варіанти того, як знайти площу трапеції
Багатолика трапеція Вона може бути довільною, равнобедренной або прямокутної. І в кожному випадку потрібно знати, як знайти площу трапеції. Звичайно,

Види трикутників. Кути трикутника
Найпростіший багатокутник, який вивчається в школі — це трикутник. Він більш зрозумілий для учнів і зустрічає менше труднощів. Незважаючи на те, що
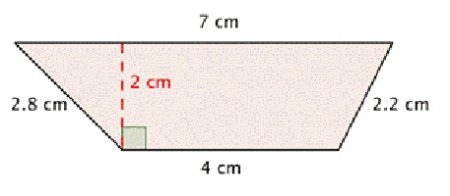
Як знайти висоту трапеції: формули на всі випадки життя
На просте питання «Як знайти висоту трапеції?» існує декілька відповідей, і все тому, що можуть бути надані різні вихідні величини. Тому і формули
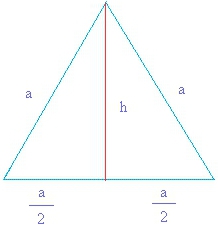
Як дізнатися площу рівностороннього трикутника: основні формули
Знайти площу рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована
