Площа підстави призми: від трикутної до багатокутної
Різні призми несхожі один на одного. У той же час у них багато спільного. Щоб знайти площу основи призми, потрібно розібратися в тому, який вигляд вона має.
Іноді в задачах фігурує висота. Вона є перпендикуляром до таких підстав. Діагоналлю багатогранника є відрізок, який з'єднує попарно дві будь-які вершини, що не належать одній грані. Слід зазначити, що площа підстави прямої призми або похилій не залежить від кута між ними і бічними гранями. Якщо у них однакові фігури у верхній і нижній гранях, то їх площі будуть рівними.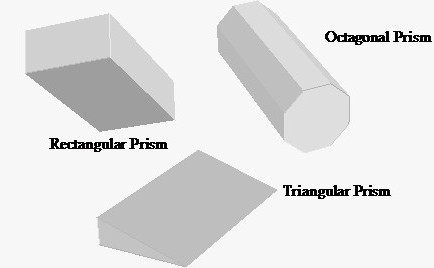
Якщо підстава — прямокутник, то його площа визначається так: S = ав, де а, в — сторони прямокутника. Коли мова йде про чотирикутної призми, то площа підстави призми обчислюється за формулою для квадрата. Тому що саме він виявляється лежачим в основі. S = а 2 . У разі коли підстава — це паралелепіпед, буде потрібно така рівність: S = а * н а . Буває таке, що дано сторона паралелепіпеда і один з кутів. Тоді для обчислення висоти потрібно скористатися додатковою формулою: н а = в * sin А. Причому кут А прилягає до сторони «в», а висота н а противолежащая до цього кутку. Якщо в основі призми лежить ромб, то для визначення його площі буде потрібна та ж формула, що для паралелограма (так як він є його окремим випадком). Але можна скористатися і такою: S = 1/2 d 1 d 2 . Тут d 1 і d 2 - дві діагоналі ромба.
Загальна теорія
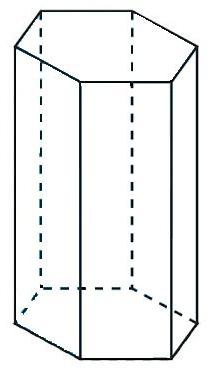
Призмою є будь-багатогранник, бічні сторони якого мають вигляд паралелограма. При цьому в її основі може виявитися будь-багатогранник - від трикутника до n-кутника. Причому підстави призми завжди дорівнюють один одному. Що не відноситься до бічним граням — вони можуть істотно відрізнятися за розмірами. При вирішенні завдань зустрічається не тільки площа основи призми. Може знадобитися знання бічній поверхні, тобто всіх граней, які не є підставами. Повною поверхнею вже буде об'єднання всіх граней, які складають призму.Іноді в задачах фігурує висота. Вона є перпендикуляром до таких підстав. Діагоналлю багатогранника є відрізок, який з'єднує попарно дві будь-які вершини, що не належать одній грані. Слід зазначити, що площа підстави прямої призми або похилій не залежить від кута між ними і бічними гранями. Якщо у них однакові фігури у верхній і нижній гранях, то їх площі будуть рівними.

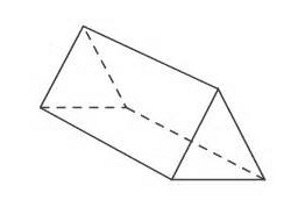
Трикутна призма
Вона має в основі фігуру, яка має три вершини, тобто трикутник. Він, як відомо, буває різним. Якщо трикутник прямокутний, то досить згадати, що його площа визначається половиною твори катетів. Математична запис виглядає так: S = 1/2 ав. Щоб дізнатися площа основи трикутної призми в загальному вигляді, знадобляться формули Герона і та, в якій береться половина сторони на висоту, проведену до неї. Перша формула повинна бути записана так: S = ?(р (р-а) (р-в) (р-с)). У цьому записі присутній півпериметр (р), тобто сума трьох сторін, поділена на два. Друга: S = 1/2 н а * а. Якщо потрібно дізнатися площа основи трикутної призми, яка є правильною, то трикутник виявляється рівностороннім. Для нього існує своя формула: S = 1/4 а 2 * ?3.
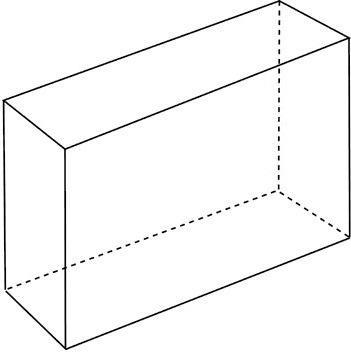
Чотирикутна призма
Її підставою є будь-який з відомих чотирикутників. Це може бути прямокутник або квадрат, паралелепіпед або ромб. В кожному випадку для того, щоб обчислити площу підстави призми, буде потрібна своя формула.Якщо підстава — прямокутник, то його площа визначається так: S = ав, де а, в — сторони прямокутника. Коли мова йде про чотирикутної призми, то площа підстави призми обчислюється за формулою для квадрата. Тому що саме він виявляється лежачим в основі. S = а 2 . У разі коли підстава — це паралелепіпед, буде потрібно така рівність: S = а * н а . Буває таке, що дано сторона паралелепіпеда і один з кутів. Тоді для обчислення висоти потрібно скористатися додатковою формулою: н а = в * sin А. Причому кут А прилягає до сторони «в», а висота н а противолежащая до цього кутку. Якщо в основі призми лежить ромб, то для визначення його площі буде потрібна та ж формула, що для паралелограма (так як він є його окремим випадком). Але можна скористатися і такою: S = 1/2 d 1 d 2 . Тут d 1 і d 2 - дві діагоналі ромба.

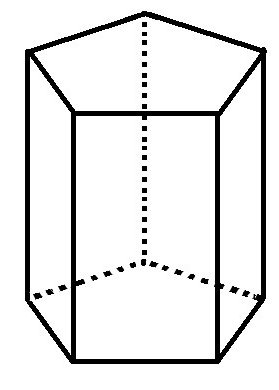
Правильна п'ятикутна призма
Цей випадок передбачає розбиття багатокутника на трикутники, площі яких дізнатися простіше. Хоча буває, що фігури можуть бути з іншою кількістю вершин. Оскільки основа призми — правильний п'ятикутник, то він може бути поділений на п'ять рівносторонніх трикутників. Тоді площа основи призми дорівнює площі одного такого трикутника (формулу можна подивитися вище), помноженій на коефіцієнт п'ять.
Правильна шестикутна призма
За принципом, описаним для п'ятикутної призми, вдається розбити шестикутник підстави на 6 рівносторонніх трикутників. Формула площі підстави такої призми подібна до попередньої. Тільки в неї площа рівностороннього трикутника слід множити на шість. Формула буде виглядати таким чином: S = 3/2 а 2 * ?3.
Завдання
№ 1. Дана правильна пряма чотирикутна призма. Її діагональ дорівнює 22 см, висота багатогранника — 14 см. Обчислити площу основи призми і всій поверхні. Рішення. Основою призми є квадрат, але його сторона не відома. Знайти її значення можна з діагоналі квадрата (х), яка пов'язана з діагоналлю призми (d) і її висотою (н). х 2 = d 2 - н 2 . З іншого боку, цей відрізок «х» є гіпотенузою в трикутник, катети якого дорівнюють стороні квадрата. Тобто х 2 = а 2 + а 2 . Таким чином виходить, що а 2 = (d 2 - н 2 )/2. Підставити замість d число 22 а «н» замінити його значенням — 14 то виходить, що сторона квадрата дорівнює 12 см. Тепер просто дізнатися площа підстави: 12 * 12 = 144 см 2 . Щоб дізнатися площа всієї поверхні, потрібно скласти подвоєне значення площі основи і учетверенную бічну. Останню легко знайти за формулою для прямокутника: перемножити висоту багатогранника і сторону основи. Тобто 14 та 12 це число буде дорівнює 168 см 2 . Загальна площа поверхні призми виявляється 960 см 2 . Відповідь. Площа основи призми дорівнює 144 см 2 . Всій поверхні - 960 см 2 . № 2. Дана правильна трикутна призма. В основі лежить трикутник зі стороною 6 см. При цьому діагональ бічної грані становить 10 см. Обчислити площі: основи і бічної поверхні. Рішення. Так як правильна призма, то її підставою є рівносторонній трикутник. Тому його площа виявляється дорівнює 6 в квадраті, помноженому на 1/4 і на корінь квадратний з 3. Просте обчислення приводить до результату: 9?3 см 2 . Це площа однієї підстави призми. Всі бічні грані однакові і являють собою прямокутники зі сторонами 6 і 10 см. Щоб обчислити їх площі, достатньо перемножити ці числа. Потім помножити їх на три, бо бічних граней призми у саме стільки. Тоді площа бічної поверхні виявляється раною 180 см 2 . Відповідь. Площі: підстави - 9?3 см 2 , бічної поверхні призми - 180 см 2 .Схожі добрі поради по темі
Як обчислити площу піраміди: підстави, бічну і повну?
При підготовці до ЄДІ з математики учням доводиться систематизувати знання з алгебри та геометрії. Хочеться об'єднати всі відомості, наприклад, про

Як раніше називали Молуккські острови?
Молуккські острови – воістину райське місце на землі, що характеризується мальовничою природою в усьому її різноманітті. Пейзажі Молуккських островів
Прямокутна трапеція: всі формули та приклади завдань
Завдання з трапецією не здаються складними в ряді фігур, які вивчені раніше. Як окремий випадок розглядається прямокутна трапеція. А при пошуку її
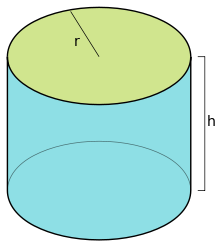
Приклади того, як обчислити площу циліндра
Існує велика кількість задач, пов'язаних з циліндром. У них потрібно знаходити радіус і висоту тіла або його вигляд перерізу. Плюс до всього, іноді
Всі тонкощі того, як обчислити площу паралелепіпеда
Паралелепіпед - найпоширеніша фігура з тих, що оточують людей. Більшість приміщень являють собою саме його. Особливо важливо знати площа
Всі варіанти того, як знайти площу трапеції
Багатолика трапеція Вона може бути довільною, равнобедренной або прямокутної. І в кожному випадку потрібно знати, як знайти площу трапеції. Звичайно,
