Всі тонкощі того, як обчислити площу паралелепіпеда
Паралелепіпед - найпоширеніша фігура з тих, що оточують людей. Більшість приміщень являють собою саме його. Особливо важливо знати площа паралелепіпеда, хоча б його бічних граней, під час ремонту. Адже потрібно точно знати, скільки матеріалу придбати.
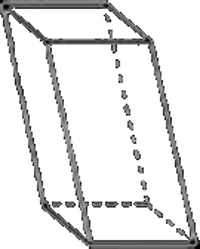 Прямий. Паралелепіпед, бічні грані якого є прямокутниками, а в основі лежить фігура з довільними величинами кутів. Прямокутний. Окремий випадок попереднього виду: в його основі знаходиться прямокутник.
Прямий. Паралелепіпед, бічні грані якого є прямокутниками, а в основі лежить фігура з довільними величинами кутів. Прямокутний. Окремий випадок попереднього виду: в його основі знаходиться прямокутник. 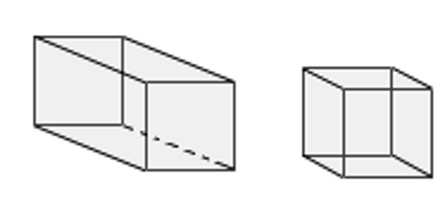 Куб. Особливий тип прямого паралелепіпеда, в якому всі грані представлені квадратами.
Куб. Особливий тип прямого паралелепіпеда, в якому всі грані представлені квадратами. Межі, які лежать навпроти один одного, не тільки паралельні, а й рівні. Діагоналі паралелепіпеда точкою перетину діляться на рівні частини. Більш загальний випадок, якщо відрізок з'єднує дві точки на поверхні тіла і проходить через точку перетину діагоналей, то він ділиться цією точкою навпіл. Для прямокутного паралелепіпеда справедливо рівність, в якому в одній його частині варто квадрат діагоналі, а в іншій - сума квадратів його висоти, ширини і довжини. 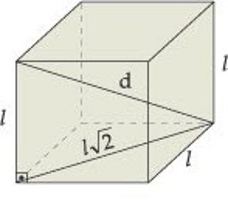
В останньому записі S ос ., тобто площа основи паралелепіпеда, може бути обчислена за формулою паралелограма. Іншими словами, потрібно вираз, в якому потрібно перемножити бік і висоту, опущену на неї.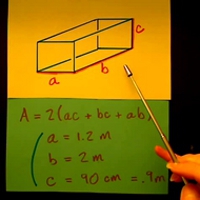
S пліч = 2 * с * (а + в) Щоб обчислити повну площу прямокутного паралелепіпеда, потрібно таке вираз: S = 2 * (ав + вс + ас) Якщо виявиться необхідним дізнатися площа його основи, то досить згадати, що це прямокутник, а значить, достатньо помножити «а» і «в».
А з-за того, що його підстави - такі ж квадрати, повна площа визначиться за формулою: S = 6 * а 2

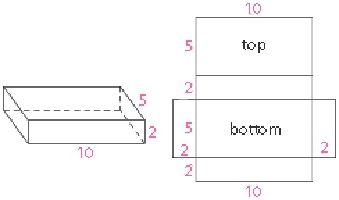 Завдання третє. Умова . Дана правильна чотирикутна призма зі стороною підстави 20 дм. Необхідно знайти її бічне ребро. Відомо, що площа паралелепіпеда дорівнює 1760 дм 2 . Рішення. Починати міркування потрібно з формули для площі всієї поверхні тіла. Тільки в ній потрібно врахувати, що ребра «а» і «в» рівні. Це випливає з твердження про те, що правильна призма. Значить, в його основі лежить чотирикутник з рівними сторонами. Звідси а = в = 20 дм. Враховуючи цю обставину, формула площі спроститься до такої: S = 2 * (а 2 + 2єс). В нею відомо все, крім шуканої величини «з», яка як раз і є бічним ребром паралелепіпеда. Щоб його знайти, потрібно виконати перетворення:
Завдання третє. Умова . Дана правильна чотирикутна призма зі стороною підстави 20 дм. Необхідно знайти її бічне ребро. Відомо, що площа паралелепіпеда дорівнює 1760 дм 2 . Рішення. Починати міркування потрібно з формули для площі всієї поверхні тіла. Тільки в ній потрібно врахувати, що ребра «а» і «в» рівні. Це випливає з твердження про те, що правильна призма. Значить, в його основі лежить чотирикутник з рівними сторонами. Звідси а = в = 20 дм. Враховуючи цю обставину, формула площі спроститься до такої: S = 2 * (а 2 + 2єс). В нею відомо все, крім шуканої величини «з», яка як раз і є бічним ребром паралелепіпеда. Щоб його знайти, потрібно виконати перетворення: розділити всі нерівність 2; потім перенести доданки так, щоб зліва виявилося доданок 2єс, а праворуч - поділена на 2 площа і квадрат «а», причому останній буде зі знаком «-»; потім поділити рівність на 2а. У підсумку вийде вираз: з = (S/2 - а 2 ) /(2а) Після підстановки всіх відомих величин і виконання дій виходить, що бічне ребро дорівнює 12 дм. Відповідь . Бічне ребро «з» дорівнює 12 дм. Завдання четверте. Умова. Дано прямокутний паралелепіпед. Одна із його граней має площу, рівну 12 см 2 . Необхідно обчислити довжину ребра, яке перпендикулярно цій межі. Додаткова умова: об'єм тіла дорівнює 60 см 3 . Рішення. Нехай відома площа тієї межі, яка розташована обличчям до спостерігачеві. Якщо прийняти за стандартні позначення літери для вимірювань паралелепіпеда, то на підставі ребра будуть «а» і «в», вертикальне - «з». Виходячи з цього, площа відомої межі визначиться як твір «а» на «с». Тепер потрібно скористатися відомим об'ємом. Його формула для прямокутного паралелепіпеда дає твір всіх трьох величин: «а», «в» і «с». Тобто відома площа, помножена на «в», дає обсяг. Звідси виходить, що шукане ребро можна обчислити з рівняння: 12 * в = 60. Елементарний розрахунок дає результат 5. Відповідь. Шукане ребро дорівнює 5 см. Завдання п'яте. Умова. Дан прямий паралелепіпед. В його основі лежить паралелограм зі сторонами 6 і 8 см, гострий кут між якими дорівнює 30o. Бічне ребро має довжину 5 см. Потрібно обчислити повну площу паралелепіпеда. Рішення. Це той випадок, коли потрібно дізнатися площі всіх граней окремо. Або, точніше, трьох пар: заснування і дві бічні. Оскільки в основі розташований паралелограм, то його площа обчислюється як добуток сторони на висоту до неї. Сторона відома, а висота - ні. Її потрібно порахувати. Для цього потрібно значення гострого кута. Висота утворює в параллелограмме прямокутний трикутник. У ньому катет дорівнює добутку синуса гострого кута, який йому противолежит, на гіпотенузу. Нехай відома сторона паралелограма - це «а». Тоді висота буде записана як в * sin 30o. Таким чином, площа основи дорівнює а * в * sin 30o. З бічними гранями все простіше. Вони - прямокутники. Тому їх площі - це твір одного боку на іншу. Перша — а*, друга — * с. Залишилося об'єднати в одну формулу і порахувати: S = 2 * (а * в * sin 30o + а * з + в * с ) Після підстановки всіх величин виходить, що шукана площа дорівнює 188 см 2 . Відповідь. S = 188 см 2 .
Що він собою являє?
Це призма з чотирикутним підставою. Тому у неї чотири бічні грані, які є параллелограммами. Тобто таке тіло має всього 6 граней. Для визначення паралелепіпеда в просторі у нього визначають площу і об'єм. Перша може бути як окремо для кожної грані, так і для всієї поверхні. До того ж виділяють ще і площа тільки бічних граней.Які існують види паралелепіпедів?
Похилий. Такий, у якого бокові грані утворюють з основою кут, відмінний від 90 градусів. У нього верхній і нижній чотирикутники не лежать один навпроти одного, а зрушені.

Деякі математичні особливості паралелепіпеда
Може виникнути ситуація, коли вони виявляться корисними в тому, щоб знайти площу паралелепіпеда.
Площі прямого паралелепіпеда
Якщо позначити висоту тіла як «н», а периметр основи буквою Р ос , то вся бічна поверхня може бути обчислена за формулою: S пліч = Р ос * н Використовуючи цю формулу і визначивши площу основи, можна порахувати повну площа: S = S пліч + 2 * S осВ останньому записі S ос ., тобто площа основи паралелепіпеда, може бути обчислена за формулою паралелограма. Іншими словами, потрібно вираз, в якому потрібно перемножити бік і висоту, опущену на неї.

Площі прямокутного паралелепіпеда
Прийнято стандартне позначення довжини, ширини і висоти такого тіла літерами «а», «в» і «с» відповідно. Площа бічної поверхні буде виражатися формулою:S пліч = 2 * с * (а + в) Щоб обчислити повну площу прямокутного паралелепіпеда, потрібно таке вираз: S = 2 * (ав + вс + ас) Якщо виявиться необхідним дізнатися площа його основи, то досить згадати, що це прямокутник, а значить, достатньо помножити «а» і «в».
Площі куба
Його бічна поверхня утворена чотирма квадратами. Значить, щоб її знайти, потрібно скористатися відомою для квадрата формулою і помножити її на чотири. S пліч = 4 * а 2А з-за того, що його підстави - такі ж квадрати, повна площа визначиться за формулою: S = 6 * а 2

Площі похилого паралелепіпеда
Оскільки його межі - це паралелограми, то потрібно дізнатися площа кожного з них і потім скласти. На щастя, противолежащие рівні. Тому обчислювати площі потрібно тільки три рази, а потім помножити їх на два. Якщо записати це у вигляді формули, то вийде наступне: S пліч = (S 1 + S 2 ) * 2 S = (S 1 + S 2 + S 3 ) * 2 Тут S 1 і S 2 є площами двох бічних граней, а S 3 - підстави.Завдання по темі
Завдання перше. Умова. Необхідно дізнатися довжину діагоналі куба, якщо площа всій його поверхні дорівнює 200 мм 2 . Рішення. Почати потрібно з отримання виразу для шуканої величини. Її квадрат дорівнює трьом квадратах сторони куба. Це означає, що діагональ дорівнює «а», помноженої на корінь з 3. Але сторона куба невідома. Тут потрібно скористатися тим, що відома площа всієї поверхні. З формули виходить, що «а» дорівнює квадратному кореню з приватного S і 6. Залишилося тільки порахувати. Ребро куба виявляється рівним (200/6), що дорівнює 10/3 (мм). Тоді діагональ вийде рівною(10/3) * 3 = 10 (мм). Відповідь. Діагональ куба дорівнює 10 мм. Завдання друге. Умова. Необхідно обчислити площу поверхні куба, якщо відомо, що його об'єм дорівнює 343 см 2 . Рішення. Потрібно скористатися тією ж формулою для площі куба. В ній знову невідомо ребро тіла. Але зате даний обсяг. З формули для куба дуже просто дізнатися «а». Воно буде дорівнює кореню кубічному з 343. Простий підрахунок дає таке значення для ребра: а = 7 см. Тепер залишилося тільки порахувати його квадрат і помножити на 6. а 2 = 7 2 = 49 звідси площа виявиться рівною 49 * 6 = 294 (см 2 ). Відповідь. S = 294 см 2 .
Схожі добрі поради по темі
Як обчислити площу піраміди: підстави, бічну і повну?
При підготовці до ЄДІ з математики учням доводиться систематизувати знання з алгебри та геометрії. Хочеться об'єднати всі відомості, наприклад, про
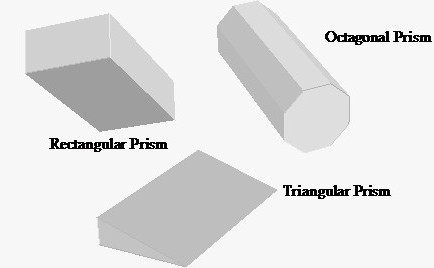
Площа підстави призми: від трикутної до багатокутної
Різні призми несхожі один на одного. У той же час у них багато спільного. Щоб знайти площу основи призми, потрібно розібратися в тому, який вигляд
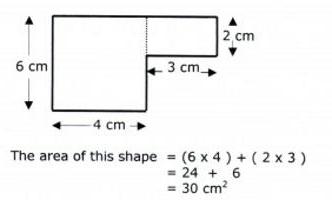
Як порахувати площу прямокутника: практичні поради
Одна з перших формул, яка вивчається в математиці, пов'язана з тим, як порахувати площу прямокутника. Вона ж є і найбільш часто використовуваною.

Іграшки з підручних матеріалів своїми руками
Радувати свого малюка хочеться кожен день. Але як бути, коли коштів постійно купувати нові іграшки не вистачає? Вихід є – зробити іграшки з підручних

Коли вийде «На грані» 2 сезон? - Дата виходу.
Новий серіал «На грані» розповідає про непростий період для кожного з жителів планети. Адже і армія, і уряд США прикладають Детальніше ->
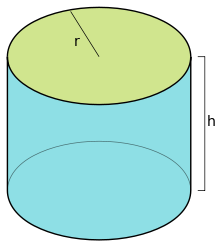
Приклади того, як обчислити площу циліндра
Існує велика кількість задач, пов'язаних з циліндром. У них потрібно знаходити радіус і висоту тіла або його вигляд перерізу. Плюс до всього, іноді
