Як знайти висоту трапеції: формули на всі випадки життя
На просте питання «Як знайти висоту трапеції?» існує декілька відповідей, і все тому, що можуть бути надані різні вихідні величини. Тому і формули будуть відрізнятися. Ці формули можна запам'ятати, але вони нескладно виводяться. Потрібно тільки застосовувати раніше вивчені теореми.
довільна трапеція
равнобедренная трапеція
назва
а
а
нижня основа
у
у
верхнє підставу
з, d
з
бокові сторони
н
н
висота
m
m
середня лінія
d 1 , d 2
d 1
діагоналі
s
s
площа
,
кути при нижньому підставі
,
,
кути на перетині діагоналей
н = (з 2 - (((а - в) 2 + з 2 - d 2 )/(2(а - в))) 2 ). Номер 1. Не найкоротша, але і зустрічається в задачах досить рідко. Зазвичай можна скористатися іншими даними. Формула, яка підкаже, як знайти висоту равнобедренной трапеції в тій же ситуації, набагато коротше: н = (з 2 - (а - в) 2 /4). Номер 2.
н = (d 1 * d 2 * sin ) /(а + в) або н = (d 1 * d 2 * sin ) /(а + в). Номер 5. Це для загального вигляду фігури. Якщо дана равнобедренная, то запис перетвориться так: н = (d 1 2 * sin ) /(а + в) або н = (d 1 2 * sin ) /(а + в). Номер 6. Коли в задачі йдеться про середньої лінії трапеції, то формули для пошуку її висоти стають такими: н = (d 1 * d 2 * sin ) /2m або н = (d 1 * d 2 * sin ) /2m. Номер 5а. н = (d 1 2 * sin ) /2m або н = (d 1 2 * sin ) /2m. Номер 6а.
Потрібно провести висоти з вершин В і С. Точки, які вкажуть кінці висот будуть позначені Н 1 і Н 2 , відповідно. Оскільки у фігурі ВСН 1 Н 2 всі кути прямі, то вона є прямокутником. Це означає, що відрізок Н 1 Н 2 дорівнює 6 см. Тепер потрібно розглянути два трикутника. Вони рівні, так як є прямокутними з однаковими гипотенузами і вертикальними катетами. Звідси випливає, що і менші катети у них рівні. Тому їх можна визначити як приватне від різниці. Остання вийде від вирахування з нижньої основи верхнього. Ділитися воно буде на 2. Тобто 12 - 6 потрібно поділити на 2. АН 1 = Н 2 Д = 3 (см). Тепер з теореми Піфагора потрібно знайти висоту трапеції. Вона необхідна для знаходження синуса кута. ВН 1 = (5 2 - 3 2 ) = 4 (см). Скориставшись знанням про те, як синус гострого кута трикутник з прямим кутом, можна записати такий вираз: sin = ВН 1 /АВ = 08. Відповідь. Шуканий синус дорівнює 08. №2. На знаходження висоти трапеції за відомим тангенсу. Умова. У равнобедренной трапеції потрібно обчислити висоту. Відомо, що її основи дорівнюють 15 і 28 см. Дан тангенс гострого кута: 11/13. Рішення. Позначення вершин таке ж, як у попередній задачі. Знову потрібно провести дві висоти з верхніх кутів. За аналогією з рішенням першої задачі потрібно знайти АН 1 = Н 2 Д, які визначаться як різниця 28 і 15 поділена на два. Після підрахунків виходить: 65 см. Оскільки тангенс — це відношення двох катетів, то можна записати таке рівняння: tg = АН 1 /ВН 1 . Причому це відношення дорівнює 11/13 (за умовою). Так як АН 1 відомий, то можна обчислити висоту: ВН 1 = (11 * 65) /13. Прості розрахунки дають результат у 55 см. Відповідь. Шукана висота дорівнює 55 см. №3. На обчислення висоти за відомим діагоналях. Умова. Про трапеції відомо, що її діагоналі дорівнюють 13 і 3 см. Потрібно дізнатися її висоту, якщо сума підстав становить 14 см. Рішення. Нехай позначення фігури буде таким же, як раніше. Припустимо, що АС — менша діагональ. З вершини потрібно провести шукану висоту і позначити її СН. Тепер потрібно виконати додаткове побудова. З кута потрібно провести пряму, паралельну більшої діагоналі і знайти точку її перетину з продовженням боку АТ. Це буде Д 1 . Вийшла нова трапеція, всередині якої накреслено трикутник АСД 1 . Він-то і потрібен для подальшого розв'язання задачі. Шукана висота виявиться ще і їй же в трикутнику. Тому можна скористатися формулами, вивченими в іншій темі. Висота трикутника визначається як добуток числа 2 і площі, поділена на сторону, до якої вона проведена. А сторона виявляється дорівнює сумі підстав вихідної трапеції. Це виходить з правила, за яким виконано додаткове побудова. У цьому трикутнику всі сторони відомі. Для зручності введемо позначення х = 3 см, у = 13 см, z = 14 см. Тепер можна порахувати площу, скориставшись теоремою Герона. Півпериметр буде дорівнює р = (х + у + z)/2 = (3 + 13 + 14) /2 = 15 (см). Тоді формула для площі після підстановки значень буде виглядати так: S= (15 * (15 - 3) * (15 - 13) * (15 - 14)) = 610 (см 2 ). Тепер потрібно порахувати висоту: н= (2 * 610) /14 = 610 /7 (см). Відповідь. Висота дорівнює 610 /7 см. №4. Для пошуку висоти по сторонам. Умова. Дана трапеція, три сторони якого дорівнюють 10 см, а четверта 24 см. Потрібно дізнатися її висоту. Рішення. Оскільки фігура равнобедренная, то потрібно формула під номером 2. У неї потрібно просто підставити всі значення і порахувати. Це буде виглядати так: н = (10 2 - (10 - 24) 2 /4) = 51 (см). Відповідь. н = 51 см.
№4. Для пошуку висоти по сторонам. Умова. Дана трапеція, три сторони якого дорівнюють 10 см, а четверта 24 см. Потрібно дізнатися її висоту. Рішення. Оскільки фігура равнобедренная, то потрібно формула під номером 2. У неї потрібно просто підставити всі значення і порахувати. Це буде виглядати так: н = (10 2 - (10 - 24) 2 /4) = 51 (см). Відповідь. н = 51 см.
Прийняті позначення у формулах
У всіх наведених нижче математичних записах вірні такі прочитання букв.довільна трапеція
равнобедренная трапеція
назва
а
а
нижня основа
у
у
верхнє підставу
з, d
з
бокові сторони
н
н
висота
m
m
середня лінія
d 1 , d 2
d 1
діагоналі
s
s
площа
,
кути при нижньому підставі
,
,
кути на перетині діагоналей
У вихідних даних: всі сторони
Для того, щоб знайти висоту трапеції в загальному випадку потрібно скористатися такою формулою:н = (з 2 - (((а - в) 2 + з 2 - d 2 )/(2(а - в))) 2 ). Номер 1. Не найкоротша, але і зустрічається в задачах досить рідко. Зазвичай можна скористатися іншими даними. Формула, яка підкаже, як знайти висоту равнобедренной трапеції в тій же ситуації, набагато коротше: н = (з 2 - (а - в) 2 /4). Номер 2.
У задачі дано: бокові сторони і кути при нижньому підставі
Приймають, що кут прилягає до бічної сторони з позначенням «з», відповідно кут стороні d. Тоді формула для того, як знайти висоту трапеції, в загальному вигляді буде такою: н = з * sin = d * sin . Номер 3. Якщо фігура равнобедренная, то можна скористатися таким варіантом: н = з * sin = ((а - в) /2) * tg . Номер 4.Відомі: діагоналі і кути між ними
Зазвичай до цих даних приєднуються ще відомі величини. Наприклад, заснування або середня лінія. Якщо дані підстави, то для відповіді на питання, як знайти висоту трапеції, стане в нагоді така формула:н = (d 1 * d 2 * sin ) /(а + в) або н = (d 1 * d 2 * sin ) /(а + в). Номер 5. Це для загального вигляду фігури. Якщо дана равнобедренная, то запис перетвориться так: н = (d 1 2 * sin ) /(а + в) або н = (d 1 2 * sin ) /(а + в). Номер 6. Коли в задачі йдеться про середньої лінії трапеції, то формули для пошуку її висоти стають такими: н = (d 1 * d 2 * sin ) /2m або н = (d 1 * d 2 * sin ) /2m. Номер 5а. н = (d 1 2 * sin ) /2m або н = (d 1 2 * sin ) /2m. Номер 6а.
Серед відомих величин: площа з підставами або середньою лінією
Це, мабуть, найбільш короткі і прості формули того, як знайти висоту трапеції. Для довільної фігури вона буде такою: н = 2S /(а + в). Номер 7. Вона ж, але з певною середньою лінією: н = S /m. Номер 7а. Як не дивно, але для равнобедренной формули трапеції будуть виглядати так само.Завдання
№1. На визначення кутів при нижньому підставі трапеції. Умова. Дана равнобедренная трапеція, бічна сторона якої 5 см. Її основи дорівнюють 6 і 12 см. Потрібно знайти синус гострого кута. Рішення. Для зручності слід ввести позначення. Нехай ліва нижня вершина буде А всі інші за годинниковою стрілкою: В, С, Д. Таким чином, нижня основа буде позначено АТ, верхнє — НД.Потрібно провести висоти з вершин В і С. Точки, які вкажуть кінці висот будуть позначені Н 1 і Н 2 , відповідно. Оскільки у фігурі ВСН 1 Н 2 всі кути прямі, то вона є прямокутником. Це означає, що відрізок Н 1 Н 2 дорівнює 6 см. Тепер потрібно розглянути два трикутника. Вони рівні, так як є прямокутними з однаковими гипотенузами і вертикальними катетами. Звідси випливає, що і менші катети у них рівні. Тому їх можна визначити як приватне від різниці. Остання вийде від вирахування з нижньої основи верхнього. Ділитися воно буде на 2. Тобто 12 - 6 потрібно поділити на 2. АН 1 = Н 2 Д = 3 (см). Тепер з теореми Піфагора потрібно знайти висоту трапеції. Вона необхідна для знаходження синуса кута. ВН 1 = (5 2 - 3 2 ) = 4 (см). Скориставшись знанням про те, як синус гострого кута трикутник з прямим кутом, можна записати такий вираз: sin = ВН 1 /АВ = 08. Відповідь. Шуканий синус дорівнює 08. №2. На знаходження висоти трапеції за відомим тангенсу. Умова. У равнобедренной трапеції потрібно обчислити висоту. Відомо, що її основи дорівнюють 15 і 28 см. Дан тангенс гострого кута: 11/13. Рішення. Позначення вершин таке ж, як у попередній задачі. Знову потрібно провести дві висоти з верхніх кутів. За аналогією з рішенням першої задачі потрібно знайти АН 1 = Н 2 Д, які визначаться як різниця 28 і 15 поділена на два. Після підрахунків виходить: 65 см. Оскільки тангенс — це відношення двох катетів, то можна записати таке рівняння: tg = АН 1 /ВН 1 . Причому це відношення дорівнює 11/13 (за умовою). Так як АН 1 відомий, то можна обчислити висоту: ВН 1 = (11 * 65) /13. Прості розрахунки дають результат у 55 см. Відповідь. Шукана висота дорівнює 55 см. №3. На обчислення висоти за відомим діагоналях. Умова. Про трапеції відомо, що її діагоналі дорівнюють 13 і 3 см. Потрібно дізнатися її висоту, якщо сума підстав становить 14 см. Рішення. Нехай позначення фігури буде таким же, як раніше. Припустимо, що АС — менша діагональ. З вершини потрібно провести шукану висоту і позначити її СН. Тепер потрібно виконати додаткове побудова. З кута потрібно провести пряму, паралельну більшої діагоналі і знайти точку її перетину з продовженням боку АТ. Це буде Д 1 . Вийшла нова трапеція, всередині якої накреслено трикутник АСД 1 . Він-то і потрібен для подальшого розв'язання задачі. Шукана висота виявиться ще і їй же в трикутнику. Тому можна скористатися формулами, вивченими в іншій темі. Висота трикутника визначається як добуток числа 2 і площі, поділена на сторону, до якої вона проведена. А сторона виявляється дорівнює сумі підстав вихідної трапеції. Це виходить з правила, за яким виконано додаткове побудова. У цьому трикутнику всі сторони відомі. Для зручності введемо позначення х = 3 см, у = 13 см, z = 14 см. Тепер можна порахувати площу, скориставшись теоремою Герона. Півпериметр буде дорівнює р = (х + у + z)/2 = (3 + 13 + 14) /2 = 15 (см). Тоді формула для площі після підстановки значень буде виглядати так: S= (15 * (15 - 3) * (15 - 13) * (15 - 14)) = 610 (см 2 ). Тепер потрібно порахувати висоту: н= (2 * 610) /14 = 610 /7 (см). Відповідь. Висота дорівнює 610 /7 см.

Схожі добрі поради по темі
Прямокутна трапеція: всі формули та приклади завдань
Завдання з трапецією не здаються складними в ряді фігур, які вивчені раніше. Як окремий випадок розглядається прямокутна трапеція. А при пошуку її
Всі тонкощі того, як обчислити площу паралелепіпеда
Паралелепіпед - найпоширеніша фігура з тих, що оточують людей. Більшість приміщень являють собою саме його. Особливо важливо знати площа
Всі варіанти того, як знайти площу трапеції
Багатолика трапеція Вона може бути довільною, равнобедренной або прямокутної. І в кожному випадку потрібно знати, як знайти площу трапеції. Звичайно,
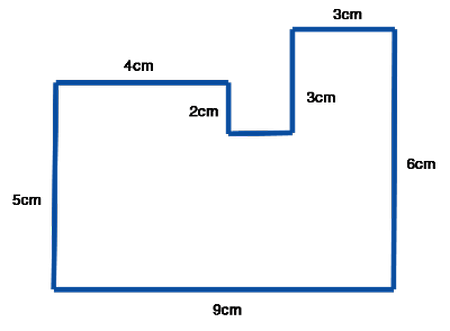
Периметр квадрата і прямокутника. Способи визначення і приклади рішення.
Часто на просторах інтернету можна знайти глузування з приводу того, як знання з математики не допомагають полегшити життя людини. Такі жарти марні,

Профорієнтація в школі та її структура
У цій статті мова піде про структурні елементи профорієнтаційної роботи: профінформації, профконсультації та профотборе, а також про заходи та
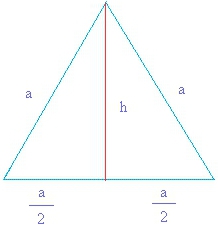
Як дізнатися площу рівностороннього трикутника: основні формули
Знайти площу рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована