Периметр квадрата і прямокутника. Способи визначення і приклади рішення.
Часто на просторах інтернету можна знайти глузування з приводу того, як знання з математики - інтеграли, диференціали, тригонометричні функції та інші розділи предмета - не допомагають полегшити життя людини. Такі жарти марні, адже як виручає уміння правильно розраховувати периметр квадрата, прямокутника та інших геометричних фігур в будівельних роботах. Витрата матеріалу: плитки, шпалер, підлогового покриття - не визначити без розуміння елементарних математичних формул і геометричних фігур.
Рівність усіх боків. Наявність чотирьох кутів величиною 90 градусів. Паралельність сторін. Поворотна симетрія. При обертанні фігури її вигляд залишається незмінним. Можливість описати і вписати окружність. Діагоналі при перетині ділять один одного навпіл. Площа фігури характеризує заповнене квадратом місце в двомірному просторі. Периметр фігури не що інше, як сума довжин його сторін. З попередньої властивості випливає, що одиницями вимірювання величини периметра будуть одиниці довжини: м, см, дм та інші. 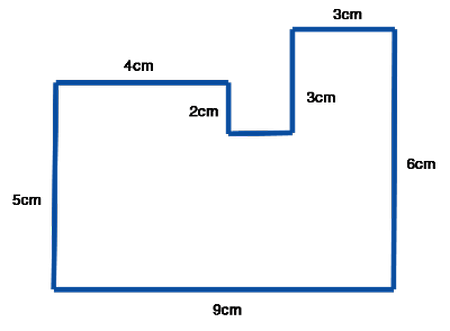
Для підрахунку плінтусів для завершення ремонту в квадратному приміщенні, необхідно знати довжину кімнати. Для цього необхідно порахувати її периметр.
Загальноприйняте позначення такої величини – літера Н. Кожній фігурі з урахуванням її властивостей притаманна своя формула для визначення периметра. Рівність протилежних сторін. Рівність діагоналей. Можливість описати окружність. Висоти прямокутника дорівнюють його сторонам. Сума кутів дорівнює 360 градусів, і всі кути прямі. Паралельність протилежних сторін. Перпендикулярність прилеглих сторін. Сума квадратів діагоналей прямокутника дорівнює сумі квадратів його сторін. Перетинаючись, діагоналі ділять один одного навпіл. Неможливість вписати в фігуру окружність. 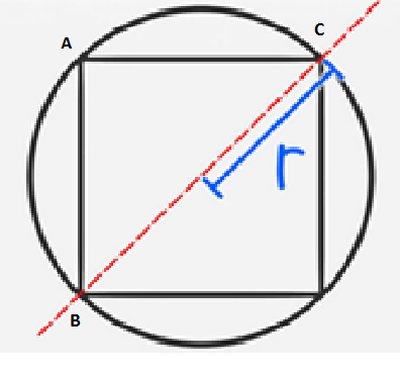 Перший варіант – знаходження периметра по радіусу описаного кола. Вписаним вважається квадрат, вершини якого знаходяться на колі. Радіус кола дорівнює 1/2 довжини діагоналі. Виходить, що діаметр дорівнює діагоналі. Тепер необхідно розглянути прямокутний трикутник, який вийшов в результаті поділу діагоналлю квадрата. Рішення задачі зводиться до знаходження сторін цього трикутника. НД – це відома величина, діаметр описаного кола. Припустимо, що він дорівнює 3 см. Теорема Піфагора у випадку з рівними сторонами трикутника, буде виглядати так: 2с 2 =3 2 . У формулі позначення с – довжина сторони трикутника і квадрата; 3 – відома величина гіпотенузи. Звідси, з=9/2. Знаючи сторону квадрата, його периметр порахувати не проблема. Особливістю вписаного кола є поділ сторін квадрата навпіл. Тому радіус дорівнює половині довжини сторони квадрата. Тоді сторона з=2*радіус. Периметр квадрата в цьому випадку дорівнює 4*2*радіус або 8 радіусах колу.
Перший варіант – знаходження периметра по радіусу описаного кола. Вписаним вважається квадрат, вершини якого знаходяться на колі. Радіус кола дорівнює 1/2 довжини діагоналі. Виходить, що діаметр дорівнює діагоналі. Тепер необхідно розглянути прямокутний трикутник, який вийшов в результаті поділу діагоналлю квадрата. Рішення задачі зводиться до знаходження сторін цього трикутника. НД – це відома величина, діаметр описаного кола. Припустимо, що він дорівнює 3 см. Теорема Піфагора у випадку з рівними сторонами трикутника, буде виглядати так: 2с 2 =3 2 . У формулі позначення с – довжина сторони трикутника і квадрата; 3 – відома величина гіпотенузи. Звідси, з=9/2. Знаючи сторону квадрата, його периметр порахувати не проблема. Особливістю вписаного кола є поділ сторін квадрата навпіл. Тому радіус дорівнює половині довжини сторони квадрата. Тоді сторона з=2*радіус. Периметр квадрата в цьому випадку дорівнює 4*2*радіус або 8 радіусах колу. 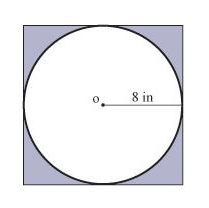
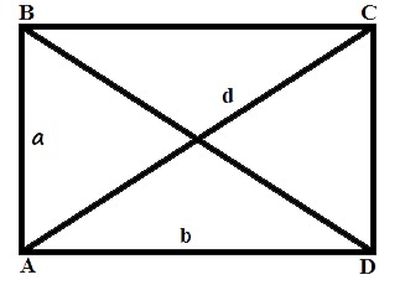 Діагональ прямокутника аналогічно квадрату ділить фігуру навпіл, утворюючи прямокутний трикутник. Проте завдання ускладнюється тим, що сторони цього трикутника нерівні. У випадку з відомою величиною однієї із сторін і діагоналі, другу можна знайти, слідуючи теоремою Піфагора: д 2 =а 2 +в 2 , де а і в – сторони фігури, а д – діагональ. Якщо невідома ні одна з сторін, тоді в справу вступають знання тригонометрії: синуси, косинуси і інші функції. Знаходження периметра по описаної окружності і відомому діаметру зводиться до того, що діаметр дорівнює довжині діагоналі фігури. Далі рішення задачі визначається по наявності відомих величин. Якщо дані кути, тоді через тригонометричні функції. Якщо дана сторона, відповідь буде знайдено через теорему Піфагора.
Діагональ прямокутника аналогічно квадрату ділить фігуру навпіл, утворюючи прямокутний трикутник. Проте завдання ускладнюється тим, що сторони цього трикутника нерівні. У випадку з відомою величиною однієї із сторін і діагоналі, другу можна знайти, слідуючи теоремою Піфагора: д 2 =а 2 +в 2 , де а і в – сторони фігури, а д – діагональ. Якщо невідома ні одна з сторін, тоді в справу вступають знання тригонометрії: синуси, косинуси і інші функції. Знаходження периметра по описаної окружності і відомому діаметру зводиться до того, що діаметр дорівнює довжині діагоналі фігури. Далі рішення задачі визначається по наявності відомих величин. Якщо дані кути, тоді через тригонометричні функції. Якщо дана сторона, відповідь буде знайдено через теорему Піфагора. 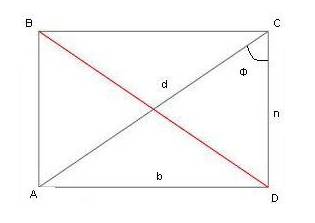 З тригонометрії необхідно згадати наступне: синус кута в прямокутному трикутнику дорівнює відношенню протилежного катета до гіпотенузі. Синус 30° (існують таблиці, за якими можна визначити значення тригонометричних функцій для правильних кутів) дорівнює 1/2. Виходить 1/2 = відношенню до d . Невідома величина буде дорівнює d /2=20/2=10 см. Для розрахунку периметра слід знайти другу сторону фігури. Можна через теорему Піфагора, так як відомі довжини гіпотенузи і одного з катетів або знову через відношення сторін для косинуса кута. Косинус кута ф виражається як відношення прилеглого катета до гіпотенузі і дорівнює 3/2. 3/2= n/d , n=(d *3)/2 або 10*3. Після вилучення кореня з 3 отримуємо довжину сторони трикутника: 10*173=173 см. Периметр дорівнює 2(173+10)=2*273=546 см.
З тригонометрії необхідно згадати наступне: синус кута в прямокутному трикутнику дорівнює відношенню протилежного катета до гіпотенузі. Синус 30° (існують таблиці, за якими можна визначити значення тригонометричних функцій для правильних кутів) дорівнює 1/2. Виходить 1/2 = відношенню до d . Невідома величина буде дорівнює d /2=20/2=10 см. Для розрахунку периметра слід знайти другу сторону фігури. Можна через теорему Піфагора, так як відомі довжини гіпотенузи і одного з катетів або знову через відношення сторін для косинуса кута. Косинус кута ф виражається як відношення прилеглого катета до гіпотенузі і дорівнює 3/2. 3/2= n/d , n=(d *3)/2 або 10*3. Після вилучення кореня з 3 отримуємо довжину сторони трикутника: 10*173=173 см. Периметр дорівнює 2(173+10)=2*273=546 см.
Властивості квадрата
Будь-які обчислення в математиці базуються на властивостях об'єкта. Щоб відповісти на питання: «Чому дорівнює периметр квадрата?» - рекомендується згадати відмінні характеристики цієї фігури.
Для підрахунку плінтусів для завершення ремонту в квадратному приміщенні, необхідно знати довжину кімнати. Для цього необхідно порахувати її периметр.
Периметр
В перекладі з грецької мови слово означає «вимірювати навколо». Термін застосовний до всіх замкнутих фігур: квадрата, кола, прямокутника, трикутника, трапеції і іншим. Знання щодо визначення периметра елементарних фігур необхідні для вирішення складних геометричних задач з об'єктами неправильної форми. Наприклад, для розрахунку плінтусів в кімнату плануванням типу «Р», або як ще називають, «чобітком», потрібно визначити периметр квадрата і прямокутника. Адже форма приміщення складається з цих елементарних фігур.Загальноприйняте позначення такої величини – літера Н. Кожній фігурі з урахуванням її властивостей притаманна своя формула для визначення периметра.
Властивості прямокутника
Периметр квадрата
В залежності від установлених (відомих) параметрів квадрата, існують різні формули для визначення його периметра. Простий завданням є розрахунок периметра при встановленій довжині його боку (з). В цьому випадку Р=с+с+с+с або 4*с. Наприклад, довжина сторони квадрата 7 см, тоді периметр фігури буде 28 см (4*7). У першому випадку все зрозуміло, але як знайти периметр квадрата, знаючи його площа? І тут все гранично ясно. Оскільки площа фігури визначається множенням одного боку на іншу, а у квадрата всі сторони рівні, необхідно витягти корінь з відомої величини. Приклад: є квадрат з площею 25 дм 2 . Корінь з 25 дорівнює 5 – ця величина характеризує довжину сторони квадрата. Тепер, підставляючи знайдену величину - 5 дм 2 - в первісну формулу периметра, можна вирішити завдання. Відповіддю буде значення в 20 дм. тобто 4 помножили на 5 отримали шукану величину.Квадрат і коло
З властивостей даної фігури випливає, що в квадрат можна вписати окружність і також її описати навколо фігури.

Периметр прямокутника
Сама елементарна формула визначення периметра прямокутника через відомі величини його сторін виглядає так: Р=2(а+b), де а і b - довжини сторін фігури.
Прямокутник і тригонометричні функції
Для наочності наведено приклад розв'язання задачі. Дано: прямокутника АВСД; довжина діагоналі ( d ) 20 см; кут ф – 30°. Знайти периметр фігури.
Периметр і відношення сторін
У шкільній програмі зустрічаються задачі з геометрії, коли довжини сторін прямокутника виражені їхнім ставленням один до одного. Розгляд рішення подібної задачі представлено нижче. Відомо, що сума довжин усіх сторін прямокутника, тобто його периметр дорівнює 84 см. Відношення довжини (д) до ширини (ш) – 3:2. Знайти сторони фігури. Рішення: нехай довжина буде 3х, а ширина 2х, згідно співвідношенню з умови задачі. Формула периметра прямокутника з отриманими даними довжин сторін буде наступною: 3х+3х+2х+2х = 84. Далі, 10х = 84 х=84 см. Підставивши х у вираз довжини і ширини прямокутника, можна знайти шукані величини. Довжина: 3*84 = 252 см; ширина: 2*84 = 168 см. Стаття присвячена вирішенню найбільш часто зустрічаються завдань у шкільній програмі. І це далеко не всі способи знаходження периметра квадрата і прямокутника.Схожі добрі поради по темі

Що таке периметр і його застосування на практиці
Не багато формули з курсу шкільної математики ми застосовуємо в повсякденному житті. Однак, є такі рівняння, які мають застосування, якщо не на
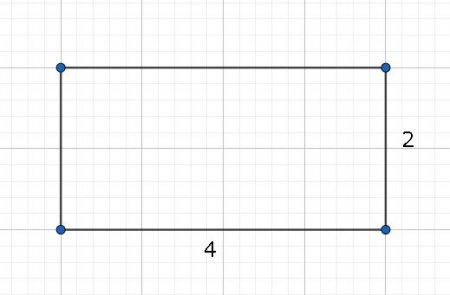
Що таке площа в математиці? Одиниці площі
Є проблеми з елементарною геометрією? Ця стаття допоможе вам вирішити одну з них. Тут ви дізнаєтеся про те, що таке площа в математиці, про одиниці

Зображення геометричних фігур для дітей
Займатися освітою своїх дітей з самого раннього віку - одна з найважливіших завдань батьків. Потрібно вчити дітей рахувати, читати невеликі
Завдання про площу квадрата і багато іншого
Такий дивовижний і знайомий квадрат. Він симетричний відносно свого центру і осей, проведених по діагоналях і через центри сторін. А шукати площа
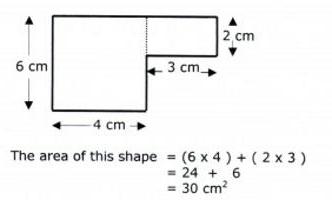
Як порахувати площу прямокутника: практичні поради
Одна з перших формул, яка вивчається в математиці, пов'язана з тим, як порахувати площу прямокутника. Вона ж є і найбільш часто використовуваною.

Геометричні фігури для дітей - розвиток дошкільників
Стаття містить інформацію про те, як розвивати образне і логічне мислення дошкільників за допомогою геометричних фігур.

