Завдання про площу квадрата і багато іншого
Такий дивовижний і знайомий квадрат. Він симетричний відносно свого центру і осей, проведених по діагоналях і через центри сторін. А шукати площа квадрата або його обсяг взагалі не становить великої праці. Особливо якщо відома довжина його сторони.
Третє пов'язано з довжиною діагоналей. Вони теж виявляються рівними один одному. Причому перетинаються під прямими кутами і в точках середини.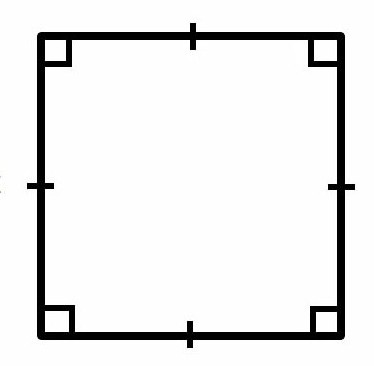
Формула в загальному вигляді виглядає так: S = (Р/4) 2 .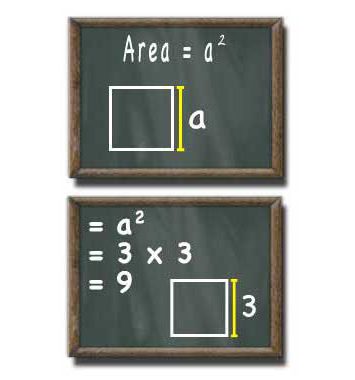 № 2. Дізнайтеся площа квадрата з периметром, рівним 32 мм. Рішення. Досить просто підставити значення периметра в написану вище формулу. Хоча можна спочатку дізнатися сторону квадрата, а вже потім його площу. В обох випадках у діях спочатку буде йти ділення, а потім зведення в ступінь. Прості розрахунки призводять до того, що площа представленого квадрата дорівнює 64 мм 2 . Відповідь. Шукана площа дорівнює 64 мм 2 . № 3. Сторона квадрата дорівнює 4 дм. Розміри прямокутника: 2 і 6 дм. У який з цих двох фігур більше площа? На скільки? Рішення. Нехай сторона квадрата буде позначена буквою а 1 , тоді довжина і ширина прямокутника а 2 і в 2 . Для визначення площі квадрата значення а 1 покладається звести в квадрат, а прямокутника — перемножити а 2 і в 2 . Це нескладно.
№ 2. Дізнайтеся площа квадрата з периметром, рівним 32 мм. Рішення. Досить просто підставити значення периметра в написану вище формулу. Хоча можна спочатку дізнатися сторону квадрата, а вже потім його площу. В обох випадках у діях спочатку буде йти ділення, а потім зведення в ступінь. Прості розрахунки призводять до того, що площа представленого квадрата дорівнює 64 мм 2 . Відповідь. Шукана площа дорівнює 64 мм 2 . № 3. Сторона квадрата дорівнює 4 дм. Розміри прямокутника: 2 і 6 дм. У який з цих двох фігур більше площа? На скільки? Рішення. Нехай сторона квадрата буде позначена буквою а 1 , тоді довжина і ширина прямокутника а 2 і в 2 . Для визначення площі квадрата значення а 1 покладається звести в квадрат, а прямокутника — перемножити а 2 і в 2 . Це нескладно.
Виходить, що площа квадрата дорівнює 16 дм 2 , а прямокутника - 12 дм 2 . Очевидно, що перша фігура більше другий. Це при тому, що вони рівнозначні, тобто мають однаковий периметр. Для перевірки можна порахувати периметри. У квадрата сторону потрібно помножити на 4 вийде 16 дм. У прямокутника скласти сторони і помножити на 2. Буде те ж число. В задачі потрібно ще відповісти, на скільки площі розрізняються. Для цього з більшого віднімають менше. Різниця виявляється рівною 4 дм 2 . Відповідь. Площі дорівнюють 16 дм 2 і 12 дм 2 . У квадрата вона більше на 4 дм 2 .
Кілька слів про фігуру і її властивості
Перші дві властивості пов'язані з визначенням. Всі сторони фігури дорівнюють один одному. Адже квадрат — це правильний чотирикутник. Причому у нього обов'язково всі сторони рівні і всі кути мають однакове значення, а саме — 90 градусів. Це друга властивість.Третє пов'язано з довжиною діагоналей. Вони теж виявляються рівними один одному. Причому перетинаються під прямими кутами і в точках середини.

Формула, в якій використовується тільки довжина сторони
Спочатку про позначенні. Для довжини сторони прийнято вибирати букву «а». Тоді площа квадрата обчислюється за формулою: S = а 2 . Вона легко виходить з того, що відома для прямокутника. В ній довжина і ширина перемножуються. У квадрата ці два елементи виявляються рівними. Тому у формулі з'являється квадрат цієї однієї величини.Формула, в якій фігурує довжина діагоналі
Вона є гіпотенузою в трикутнику, катетами якого є сторони фігури. Тому можна скористатися формулою теореми Піфагора і вивести рівність, в якому сторона виражена через діагональ. Провівши такі нескладні перетворення, отримуємо, що площа квадрата через діагональ обчислюється за такою формулою: S = d 2 /2 . Тут позначена буквою d діагональ квадрата.
Формула по периметру
У такій ситуації необхідно висловити бік через периметр і підставити його в формулу площі. Оскільки однакових сторін у чотири фігури, то периметр доведеться розділити на 4. Це буде значення сторони, яку потім можна підставити в початкову і порахувати площу квадрата.Формула в загальному вигляді виглядає так: S = (Р/4) 2 .
Задачі на розрахунки
№ 1. Є квадрат. Сума двох його сторін дорівнює 12 см. Обчисліть площу квадрата і його периметр. Рішення. Оскільки дана сума двох сторін, то потрібно дізнатися довжину однієї. Так як вони однакові, то відоме число потрібно просто поділити на два. Тобто сторона цієї фігури дорівнює 6 см. Тоді його периметр і площа легко обчислюються за наведеними формулами. Перший дорівнює 24 см, а друга - 36 см 2 . Відповідь. Периметр квадрата дорівнює 24 см, а його площа — 36 см 2 .
Виходить, що площа квадрата дорівнює 16 дм 2 , а прямокутника - 12 дм 2 . Очевидно, що перша фігура більше другий. Це при тому, що вони рівнозначні, тобто мають однаковий периметр. Для перевірки можна порахувати периметри. У квадрата сторону потрібно помножити на 4 вийде 16 дм. У прямокутника скласти сторони і помножити на 2. Буде те ж число. В задачі потрібно ще відповісти, на скільки площі розрізняються. Для цього з більшого віднімають менше. Різниця виявляється рівною 4 дм 2 . Відповідь. Площі дорівнюють 16 дм 2 і 12 дм 2 . У квадрата вона більше на 4 дм 2 .
Завдання на доказ
Умова. На катете рівнобедреного прямокутного трикутника побудований квадрат. До його гіпотенузі побудована висота, на якій побудований ще один квадрат. Довести, що площа першого в два рази більше, ніж другого. Рішення. Введемо позначення. Нехай катет дорівнює а, а висота, проведена до гіпотенузі, х. Площа першого квадрата — S 1 , другого — S 2 . Площа квадрата, побудованого на катете, обчислюється просто. Вона виявляється рівною а 2 . З другим значенням все не так просто. Для початку потрібно дізнатися довжину гіпотенузи. Для цього знадобиться формула теореми Піфагора. Прості перетворення приводять до такого виразу: а?2. Оскільки висота в равнобедренном трикутнику, проведена до основи, є ще і медіаною і висотою, то вона ділить великий трикутник на два рівних рівнобедрених прямокутних трикутника. Тому висота дорівнює половині гіпотенузи. Тобто х = (а?2)/2. Звідси легко дізнатися площа S 2 . Вона виходить рівною а 2 /2. Очевидно, що записані значення відрізняються рівно в два рази. Причому друга в це число разів менше. Що і потрібно було довести.Незвичайна головоломка — танграм
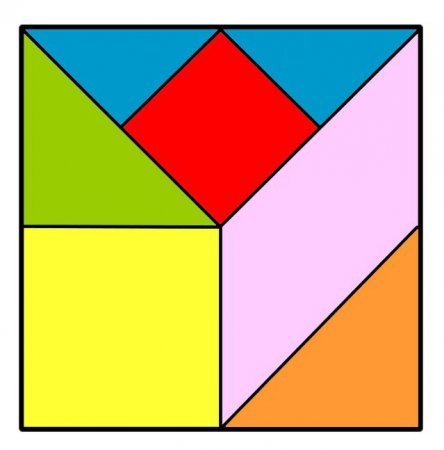
Вона робиться з квадрата. Його необхідно за певними правилами розрізати на різні фігури. Всього частин повинно виявитися 7. Правила передбачають, що в процесі гри будуть використовуватися всі отримані деталі. З них потрібно складати інші геометричні фігури. Наприклад, прямокутник, трапеція або паралелограм. Але ще цікавіше, коли з шматочків виходять силуети тварин або предметів. Причому виявляється, що площа усіх похідних фігур дорівнює тій, що була у початкового квадрата.Схожі добрі поради по темі
Як зробити паперові кораблики: кілька способів
Виготовлення будь-яких фігурок з паперу доставляє масу задоволення дітям, і особливо коли в цьому беруть участь і батьки. Існує кілька способів, як
Як обчислити площу піраміди: підстави, бічну і повну?
При підготовці до ЄДІ з математики учням доводиться систематизувати знання з алгебри та геометрії. Хочеться об'єднати всі відомості, наприклад, про
Площа підстави призми: від трикутної до багатокутної
Різні призми несхожі один на одного. У той же час у них багато спільного. Щоб знайти площу основи призми, потрібно розібратися в тому, який вигляд
Всі тонкощі того, як обчислити площу паралелепіпеда
Паралелепіпед - найпоширеніша фігура з тих, що оточують людей. Більшість приміщень являють собою саме його. Особливо важливо знати площа
Периметр квадрата і прямокутника. Способи визначення і приклади рішення.
Часто на просторах інтернету можна знайти глузування з приводу того, як знання з математики не допомагають полегшити життя людини. Такі жарти марні,
Як дізнатися площу рівностороннього трикутника: основні формули
Знайти площу рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована