Округлення чисел: цілі і дроби
Хто знає точне значення числа пі? Більшість пам'ятає, що воно дорівнює 314. Але це приблизна, а не точне значення, тому що насправді число пі являє собою неперіодичну, тобто нескінченний дріб. Тут-то і необхідно округлення чисел.
потрібно визначити, що це за число - ціле або дробове (16119; 118591); необхідно зрозуміти, до якого розряду відбувається округлення (сотні; десяті); треба знайти шуканий розряд (16119 - третій праворуч; 11854 - четвертий справа); подивитися на цифру, наступну за значенням розряду; якщо вона від 0 до 4 - значення шуканого розряду залишається колишнім, якщо 5 і більше - збільшується на одиницю; записати число в скороченому вигляді (16100; 119).
Найпростіше, коли знайдений потрібний розряд, для зручності підкреслити його. Це позбавить від плутанини, яка може виникнути спочатку. Пізніше це взагалі не знадобиться, тому що округлення чисел стане настільки простим завданням, що не буде викликати труднощів. Часто розряди десяткових чисел викликають різні труднощі. Не завжди просто з першого разу запам'ятати, що спочатку йдуть десяткові частки, потім соті, потім тисячні і десятитисячні і так далі. У зв'язку з цим округлення чисел після коми може спочатку стати причиною непередбачених складнощів. І тут слід згадати, що, як правило, про розрядах кажуть лише, коли мова йде про цілих числах. У випадку з дробовими формулювання найчастіше буває такою "округлення до n-ного знака після коми", вона зрозуміліше і зручніше для всіх. Так що боятися не варто - це зовсім не складне завдання, яка після деякої практики виявиться під силу кожному.

Що це таке?
Скільки буде, якщо 10 розділити на 3? Будь-який дорослий знає, що 333. Але на ділі це не зовсім справедливо. Результат заокруглений, і насправді значення становить нескінченна десятковий дріб. Але така запис була б кілька незручна. А враховуючи той факт, що у дробу насправді немає кінця, це й ні до чого. Іноді достатньо лише приблизних чисел - 10 замість 9,99 або 314 а не 314,1592653589Навіщо воно потрібно?
У вирішенні більшості завдань не потрібна висока точність, якщо це не вища математика. Округлення чисел треба як раз для того, щоб спростити деякі дії, якщо запис занадто довга. Це дозволяє уникнути занадто громіздких обчислень, коли не потрібен дуже точний результат.Алгоритм
Зазвичай тему "Округлення чисел" проходять у 4-5 класі. В цей час учні вже знають про десяткових дробах, вміють проводити дії з ними, розбираються в розрядах. Зазвичай округляють натуральні числа як цілі, так і дробові. Це робиться наступним чином:Найпростіше, коли знайдений потрібний розряд, для зручності підкреслити його. Це позбавить від плутанини, яка може виникнути спочатку. Пізніше це взагалі не знадобиться, тому що округлення чисел стане настільки простим завданням, що не буде викликати труднощів. Часто розряди десяткових чисел викликають різні труднощі. Не завжди просто з першого разу запам'ятати, що спочатку йдуть десяткові частки, потім соті, потім тисячні і десятитисячні і так далі. У зв'язку з цим округлення чисел після коми може спочатку стати причиною непередбачених складнощів. І тут слід згадати, що, як правило, про розрядах кажуть лише, коли мова йде про цілих числах. У випадку з дробовими формулювання найчастіше буває такою "округлення до n-ного знака після коми", вона зрозуміліше і зручніше для всіх. Так що боятися не варто - це зовсім не складне завдання, яка після деякої практики виявиться під силу кожному.

Деякі особливості
Округлення чисел можна іноді переплутати з записом періодичних дробів. Відрізнити їх легко по наявності або відсутності дужок. Ще варто звернути увагу на те, що після коми потрібно прибирати зайві нулі. Якщо в результаті округлення вийшло значення кшталт такого: 0140900 то сміливо можна не писати дві останні цифри, вони не грають ніякої ролі. У випадку, якщо число виходить нескінченним, але необхідна достатня точність, краще записати його по-іншому, наприклад у вигляді звичайного дробу або виразу. Це буде виглядати більш коротко і зручно. До речі, деякі нескінченні дробу мають власні назви. Так, всі знають числа (314) і золотий перетин (1618), а також постійну e (2718). Таких насправді дуже багато, і вони дуже активно використовуються в математиці. Їх називають ірраціональними, і в побуті вони зовсім не потрібні, але навіть вчені дуже рідко використовують їх так, щоб їм була необхідна висока точність. Точність цих чисел визначена аж до десятків і сотень тисяч після коми, і вони до цих пір залишаються загадкою для математиків усього світу, в той час як інші просто округляють їх.Схожі добрі поради по темі

Дроби: історія дробів. Історія виникнення звичайних дробів
Одним з найбільш складних розділів математики донині вважаються дробу. Історія дробів налічує не одне тисячоліття. Уміння ділити ціле на частини
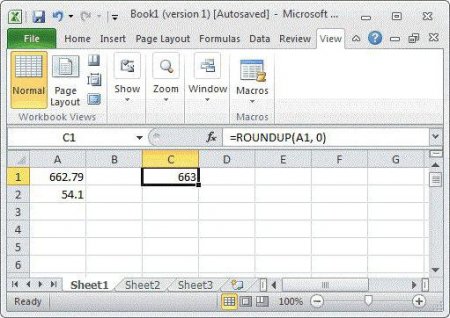
Округлення в Excel. Способи і формули
У даній статті ми розповімо про те, як правильно проводити округлення чисел і розрахунків у програмі Microsoft Office Excel.
Ділення на нуль. Захоплююча математика
Чому неможливо ділення на нуль, чим пояснити цей принцип елементарної математики? Як обходять цей принцип при вирішенні меж послідовностей?
Неправильні дроби: як навчитися вирішувати з ними приклади?
При слові "дроби" у багатьох біжать мурашки. Тому що згадується школа і завдання, які вирішувалися на математиці. Це було обов'язком, яку необхідно
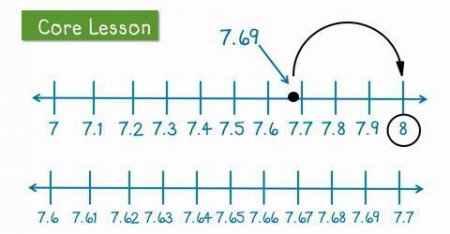
Округлення десяткових дробів: вчимося математики
Сьогодні ми з вами навчимося округлення десяткових дробів. Цей прийом допоможе в житті ще не один раз.
Комплексні числа та дії над ними
Комплексні числа не є числами в елементарному значенні цього слова, що застосовуються при підрахунках і вимірюваннях, а є математичними об'єктами,


