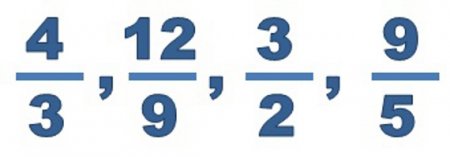Неправильні дроби: як навчитися вирішувати з ними приклади?
При слові "дроби" у багатьох біжать мурашки. Тому що згадується школа і завдання, які вирішувалися на математиці. Це було обов'язком, яку необхідно було виконати. А що якщо ставитися до завдань, що містить правильні і неправильні дроби, як до головоломці? Адже багато дорослі вирішують цифрові і японські кросворди. Розібралися в правилах, і все. Так само і тут. Варто тільки вникнути в теорію - і все стане на свої місця. А приклади перетворяться у спосіб потренувати мозок.
 Серед звичайних виділяють правильні і неправильні дроби. У перших чисельник по модулю завжди менше знаменника. Неправильні тому так і називаються, що у них все навпаки. Значення правильної дробу завжди менше одиниці. У той час як неправильна завжди більше цього числа. Є ще змішані числа, тобто такі, у яких є ціла і дробова частини. Другий вид запису — десятковий дріб. Про неї окрема розмова.
Серед звичайних виділяють правильні і неправильні дроби. У перших чисельник по модулю завжди менше знаменника. Неправильні тому так і називаються, що у них все навпаки. Значення правильної дробу завжди менше одиниці. У той час як неправильна завжди більше цього числа. Є ще змішані числа, тобто такі, у яких є ціла і дробова частини. Другий вид запису — десятковий дріб. Про неї окрема розмова.
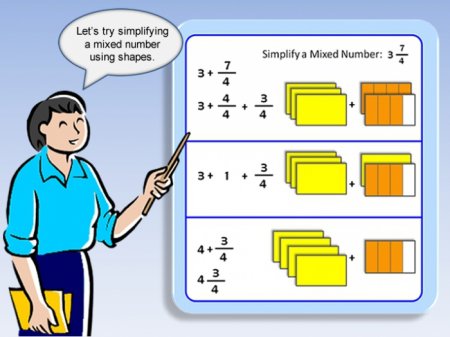
Всі залежить від конкретної ситуації. Іноді у завданнях зручніше використовувати неправильний дріб. А деколи необхідно перевести її в мішане число і тоді приклад вирішиться дуже легко. Тому, що використовувати: неправильні дроби, мішані числа, - залежить від спостережливості вирішального завдання. Змішане число ще порівнюють з сумою цілої та дробової частини. Причому друга завжди менше одиниці. знаменник помножити на цілу частину; додати до результату значення чисельника; записати відповідь над рискою; знаменник залишити той самий. Ось приклади того, як записати неправильні дроби з мішаних чисел:
17 1/4 = (17 х 4 + 1) : 4 = 69/4; 39 1/2 = (39 х 2 + 1) : 2 = 79/2. 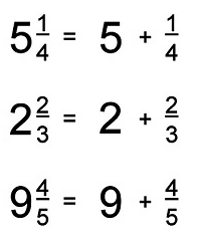
поділити чисельник на знаменник до отримання залишку; записати приватне на місці цілої частини змішаного; залишок слід розмістити над рискою; дільник буде знаменником. Приклади такого перетворення: 76/14; 76:14 = 5 із залишком 6; відповіддю буде 5 цілих і 6/14; дробову частину в цьому прикладі треба скоротити на 2 вийде 3/7; підсумковий відповідь — 5 цілих 3/7. 108/54; після поділу виходить приватне 2 без залишку; це означає, що не всі неправильні дроби вдається представити у вигляді змішаного числа; відповіддю буде ціле — 2. помножити число на потрібний знаменник; записати це значення над рискою; розмістити під нею знаменник. Найпростіший варіант, коли знаменник дорівнює одиниці. Тоді нічого множити не потрібно. Достатньо просто написати ціле число, яке дано в прикладі, а під рискою розташувати одиницю. Приклад : 5 зробити неправильної дробу зі знаменником 3. Після множення 5 на 3 виходить 15. Це число буде знаменником. Відповідь завдання дріб: 15/3.
Які види дробів існують?
Для початку про те, що це таке. Дріб — це число, яке має деяку частину від одиниці. Її можна записати у двох видах. Перший носить назву звичайної. Тобто така, у якої є горизонтальна або похила риска. Вона прирівнюється до знаку ділення. У такому записі число, що стоїть над рискою, називається чисельником, а під нею — знаменником.
Чим відрізняються неправильні дроби від змішаних чисел?
По своїй суті, нічим. Це просто різна запис одного і того ж числа. Неправильні дроби після нескладних дій легко стають змішаними числами. І навпаки.Всі залежить від конкретної ситуації. Іноді у завданнях зручніше використовувати неправильний дріб. А деколи необхідно перевести її в мішане число і тоді приклад вирішиться дуже легко. Тому, що використовувати: неправильні дроби, мішані числа, - залежить від спостережливості вирішального завдання. Змішане число ще порівнюють з сумою цілої та дробової частини. Причому друга завжди менше одиниці.
Як уявити змішане число у вигляді неправильного дробу?
Якщо потрібно виконати яку-небудь дію з кількома числами, що записані в різних видах, то потрібно зробити їх однаковими. Один з методів — представити числа у вигляді неправильних дробів. Для цієї мети потрібно виконати дії за таким алгоритмом: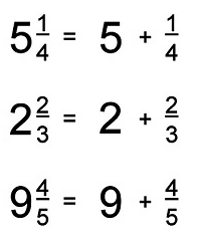
Як записати неправильний дріб у вигляді змішаного числа?
Наступний прийом протилежний розглянутому вище. Тобто коли всі мішані числа замінюються на неправильні дроби. Алгоритм дій буде таким:Як ціле число перетворити в неправильний дріб?
Бувають ситуації, коли необхідно і таку дію. Щоб отримати неправильні дроби з заздалегідь відомим знаменником, потрібно виконати такий алгоритм:Два підходи до вирішення завдань з різними числами
У прикладі потрібно обчислити суму і різницю, а також добуток і частку двох чисел: 2 цілих 3/5 і 14/11. У першому підході змішане число буде представлено у вигляді неправильного дробу. Після виконання дій, описаних вище, вийде таке значення: 13/5. Для того щоб дізнатися про суму, потрібно привести дроби до однакового знаменника. 13/5 після множення на 11 стане 143/55. А 14/11 після множення на 5 прийме вигляд: 70/55. Для обчислення суми потрібно тільки скласти чисельники: 143 і 70 а потім записати відповідь з одним знаменником. 213/55 — ця неправильна дріб відповідь задачі. При знаходженні різниці ці ж числа віднімаються: 143 - 70 = 73. Відповіддю буде дріб: 73/55. При множенні 13/5 і 14/11 не потрібно приводити до спільного знаменника. Достатньо перемножити попарно чисельники і знаменники. Вийде відповідь: 182/55. Так само і при поділі. Для правильного вирішення потрібно замінити поділ на множення і перевернути дільник: 13/5 : 14/11 = 13/5 х 11/14 = 143/70. У другому підході неправильна дріб звертається до змішане число. Після виконання дій алгоритму 14/11 звернеться в мішане число з цілою частиною 1 та дробової 3/11. Під час обчислення суми потрібно скласти цілі і дробові частини окремо. 2 + 1 = 3 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Підсумковий відповідь виходить 3 цілих 48/55. У першому підході була дріб 213/55. Перевірити правильність можна, перевівши його в мішане число. Після поділу 213 на 55 виходить приватне 3 і залишок 48. Неважко помітити, що відповідь правильна. При відніманні знак «+» замінюється на«-». 2 - 1 = 133/55 - 15/55 = 18/55. Для перевірки відповідь з попереднього підходу потрібно перевести в мішане число: 73 ділиться на 55 і виходить 1 приватне і залишок 18. Для знаходження добутку і частки користуватися змішаними числами незручно. Тут завжди рекомендується переходити до неправильним дробям.Схожі добрі поради по темі

А вам вдасться вирішити ці прості математичні приклади за 10 секунд?
Всі знають, що математика - цариця всіх наук, адже без неї неможливі всі інші науки. Завдяки математиці людям вдалося побудувати ракети і побувати в

Як переводити хвилини в години і навпаки: приклади, способи, цікаві моменти
У статті розглянуто цікаве питання про переведення годинників в хвилини хвилин до години. Дані різні приклади, способи рішення. Матеріал адресований

Дроби: історія дробів. Історія виникнення звичайних дробів
Одним з найбільш складних розділів математики донині вважаються дробу. Історія дробів налічує не одне тисячоліття. Уміння ділити ціле на частини
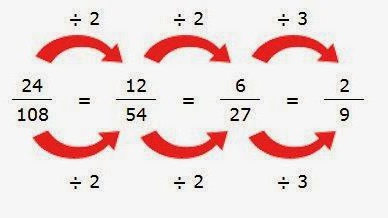
Як скорочувати дроби правильно?
Дроби та їх скорочення — ще одна тема, яка починається в 5 класі. Тут формується база цієї дії, а потім ці вміння тягнуться ниточкою у вищу
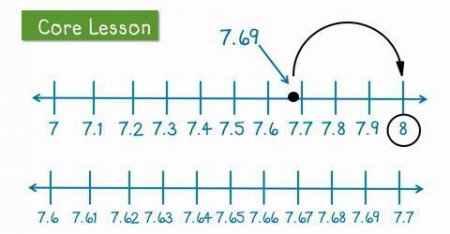
Округлення десяткових дробів: вчимося математики
Сьогодні ми з вами навчимося округлення десяткових дробів. Цей прийом допоможе в житті ще не один раз.

Округлення чисел: цілі і дроби
Тему про округлення чисел проходять ще в початковій школі. Це вміння так чи інакше постійно потрібно в побуті. Люди навіть не помічають, як