Історія теореми Піфагора. Доказ теореми
Історія теореми Піфагора налічує кілька тисячоліть. Твердження, свідчить, що квадрат гіпотенузи дорівнює сумі квадратів катетів, було відомо ще задовго до народження грецького математика. Проте теорема Піфагора, історія створення та докази її зв'язуються для більшості саме з цим ученим. Згідно з деякими джерелами, причиною тому послужило перший доказ теореми, яке було приведено Піфагором. Однак частина дослідників спростовує цей факт. 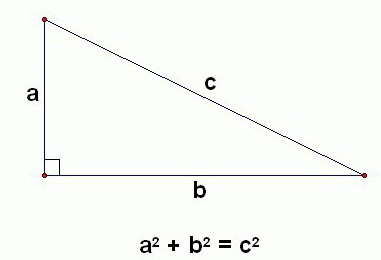

Мудрець навчався у великих умів того часу. Серед викладачів молодого Піфагора значаться Гермодамант і Ферекид Сиросский. Перший прищепив йому любов до музики, другий навчив філософії. Обидві ці науки залишаться в центрі уваги вченого протягом всього його життя.
Сьогодні не можна точно стверджувати, чи був Піфагор в Єгипті і Вавилоні. Можливо, він залишив Самос пізніше і відразу відправився в Кротоні.
Історія теореми Піфагора пов'язана з розвитком створеної грецьким філософом школи. Це релігійно-етичне братство проповідувало дотримання особливого способу життя, вивчав арифметику, геометрію та астрономію, займалося дослідженням філософської і містичної боку чисел. Всі відкриття учнів грецького математика приписувалися йому. Проте історія виникнення теореми Піфагора зв'язується стародавніми біографами тільки з самим філософом. Передбачається, що він передав грекам знання, отримані у Вавилоні та Єгипті. Є також версія, що він дійсно відкрив теорему про співвідношення катетів і гіпотенузи, не знаючи про досягнення інших народів.
Вважається, що в трактаті «Початку», створеному Евклидом, автор наводить доказ теореми, автором якого був великий грецький математик. Проте таку точку зору підтримували не всі. Так, ще античний філософ-неоплатонік Прокл вказував, що автором наведеного в «Засадах» докази є сам Евклід. Як би те ні було, але першим, хто сформулював теорему, все-таки був Піфагор.
Теорема Піфагора, історія створення якої розглядається в статті, згідно німецькому математику Кантору, була відома ще в 2300 році до н. е. в Єгипті. Стародавні жителі долини Нілу в часи правління фараона Аменемхета I знали рівність 3 2 + 4 2 = 5 2 . Передбачається, що за допомогою трикутників зі сторонами 3 4 і 5 єгипетські «натягиватели мотузок» вибудовували прямі кути. Знали теорему Піфагора і в Вавилоні. На глиняних табличках, датованих 2000 роком до н. е і відносяться до часу правління царя Хаммурапі, виявлений приблизний розрахунок гіпотенузи прямокутного трикутника. 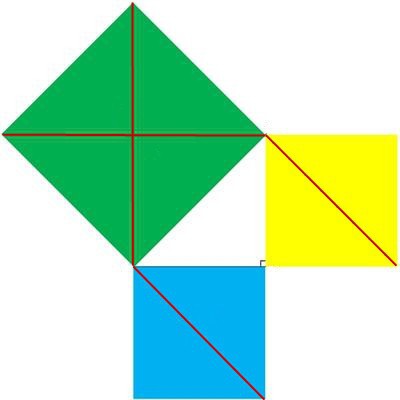
Ще одне просте доказ поєднує геометрії з алгеброю. Чотири однакових прямокутних трикутника зі сторонами а, в, с вычерчиваются так, що утворюють два квадрата: зовнішній зі стороною (а + в) і внутрішній зі стороною с. При цьому площа меншого квадрата дорівнює з 2 . Площа великого обчислюється з суми площ маленького квадрата і всіх трикутників (площа прямокутного трикутника, нагадаємо, обчислюється за формулою (а * в) /2), тобто з 2 + 4 * ((а * в) /2), що одно з 2 + 2ав. Площа великого квадрата можна обчислити й інакше — як добуток двох сторін, тобто (а + в) 2 , що дорівнює а 2 + 2ав + в 2 . Виходить: а 2 + 2ав + в 2 = з 2 + 2ав, а 2 + в 2 = з 2 .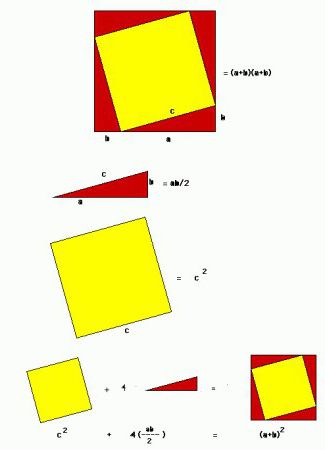 Відомо безліч варіантів доведення цієї теореми. Над ними працював і Евкліда, і індійські вчені, і Леонардо да Вінчі. Часто стародавні мудреці приводили креслення, приклади яких розташовані вище, і не супроводжували їх ніякими поясненнями, крім позначки «Дивись!» Простота геометричного доказу за умови наявності деяких знань коментарів і не вимагала. Історія теореми Піфагора, коротко викладена у статті, розвінчує міф про її походження. Однак важко навіть уявити, що ім'я великого грецького математика і філософа коли-небудь перестане асоціюватися з нею.
Відомо безліч варіантів доведення цієї теореми. Над ними працював і Евкліда, і індійські вчені, і Леонардо да Вінчі. Часто стародавні мудреці приводили креслення, приклади яких розташовані вище, і не супроводжували їх ніякими поясненнями, крім позначки «Дивись!» Простота геометричного доказу за умови наявності деяких знань коментарів і не вимагала. Історія теореми Піфагора, коротко викладена у статті, розвінчує міф про її походження. Однак важко навіть уявити, що ім'я великого грецького математика і філософа коли-небудь перестане асоціюватися з нею.

Музика і логіка
Перш ніж розповісти, як складалася історія теореми Піфагора, коротко зупинимося на біографії математика. Він жив у VI столітті до нашої ери. Датою народження Піфагора вважається 570 рік до н. е., місцем — острів Самос. Про життя вченого достовірно відомо небагато. Біографічні дані в давньогрецьких джерелах переплітаються з явним вигадкою. На сторінках трактатів він постає великим мудрецем, чудово володіє словом і умінням переконувати. До речі, саме тому грецького математика і прозвали Піфагором, тобто «котрі переконують промовою». За іншою версією, народження майбутнього мудреця передбачила Піфія. Батько в її честь назвав хлопчика Піфагором.
Мудрець навчався у великих умів того часу. Серед викладачів молодого Піфагора значаться Гермодамант і Ферекид Сиросский. Перший прищепив йому любов до музики, другий навчив філософії. Обидві ці науки залишаться в центрі уваги вченого протягом всього його життя.
Навчання довжиною в 30 років
За однією з версій, будучи допитливим юнаком, Піфагор залишив батьківщину. Він вирушив шукати знань в Єгипет, де пробув, за різними джерелами, від 11 до 22 років, а потім потрапив у полон і був відправлений у Вавилон. Піфагор зміг отримати користь з свого становища. Протягом 12 років він вивчав математику, геометрію і магію в стародавній державі. На Самос Піфагор повернувся тільки в 56 років. Тут в той час правил тиран Полікрат. Піфагор не зміг прийняти таку політичну систему і незабаром відправився на південь Італії, де розміщувалась грецька колонія Кротон.Сьогодні не можна точно стверджувати, чи був Піфагор в Єгипті і Вавилоні. Можливо, він залишив Самос пізніше і відразу відправився в Кротоні.
Піфагорійці

Теорема Піфагора: історія відкриття
В деяких давньогрецьких джерелах описується радість Піфагора, коли йому вдалося довести теорему. В честь такої події він наказав принести жертву богам у вигляді сотні биків і влаштував бенкет. Деякі вчені, однак, вказують на неможливість такого вчинку з-за особливостей поглядів піфагорійців.Вважається, що в трактаті «Початку», створеному Евклидом, автор наводить доказ теореми, автором якого був великий грецький математик. Проте таку точку зору підтримували не всі. Так, ще античний філософ-неоплатонік Прокл вказував, що автором наведеного в «Засадах» докази є сам Евклід. Як би те ні було, але першим, хто сформулював теорему, все-таки був Піфагор.
Стародавній Єгипет і Вавилон

Індія і Китай
Історія теореми Піфагора пов'язана і з древніми цивілізаціями Індії і Китаю. Трактаті «Чжоу-бі суань цзинь» містить вказівки, що єгипетський трикутник (його сторони співвідносяться як 3:4:5) був відомий в Китаї ще у XII ст. до н. е, а до VI ст. до н. е. математики цієї держави знали загальний вигляд теореми. Побудова прямого кута за допомогою єгипетського трикутника було викладено і в індійському трактаті «Сульва сутра», що датується VII-V ст. до н. е. Таким чином, історія теореми Піфагора до моменту народження грецького математика і філософа налічувало вже кілька сотень років.Доказ
За час свого існування теорема стала однією з основоположних у геометрії. Історія доведення теореми Піфагора, ймовірно, почалася з розгляду рівностороннього прямокутного трикутника. На його гіпотенузі і катетах будуються квадрати. Той, що «виріс» на гіпотенузі, буде складатися з чотирьох трикутників, рівних першому. Квадрати на катетах при цьому складаються з двох таких трикутників. Просте графічне зображення наочно показує справедливість твердження, сформульованого у вигляді знаменитої теореми.
Ще одне просте доказ поєднує геометрії з алгеброю. Чотири однакових прямокутних трикутника зі сторонами а, в, с вычерчиваются так, що утворюють два квадрата: зовнішній зі стороною (а + в) і внутрішній зі стороною с. При цьому площа меншого квадрата дорівнює з 2 . Площа великого обчислюється з суми площ маленького квадрата і всіх трикутників (площа прямокутного трикутника, нагадаємо, обчислюється за формулою (а * в) /2), тобто з 2 + 4 * ((а * в) /2), що одно з 2 + 2ав. Площа великого квадрата можна обчислити й інакше — як добуток двох сторін, тобто (а + в) 2 , що дорівнює а 2 + 2ав + в 2 . Виходить: а 2 + 2ав + в 2 = з 2 + 2ав, а 2 + в 2 = з 2 .

Схожі добрі поради по темі

Поет, що писав знаменитої віршованій "драбинкою". Трохи про Маяковського
У статті коротко аналізується творчість великого поета Ст. В. Маяковського. Саме йому належить знаменитий стиль написання віршів "драбинкою".

Дроби: історія дробів. Історія виникнення звичайних дробів
Одним з найбільш складних розділів математики донині вважаються дробу. Історія дробів налічує не одне тисячоліття. Уміння ділити ціле на частини
Завдання про площу квадрата і багато іншого
Такий дивовижний і знайомий квадрат. Він симетричний відносно свого центру і осей, проведених по діагоналях і через центри сторін. А шукати площа
Прямокутна трапеція: всі формули та приклади завдань
Завдання з трапецією не здаються складними в ряді фігур, які вивчені раніше. Як окремий випадок розглядається прямокутна трапеція. А при пошуку її
Як знайти висоту трапеції: формули на всі випадки життя
На просте питання «Як знайти висоту трапеції?» існує декілька відповідей, і все тому, що можуть бути надані різні вихідні величини. Тому і формули
Як дізнатися площу рівностороннього трикутника: основні формули
Знайти площу рівностороннього трикутника можна за будь-якою формулою для довільної фігури даного типу або скористатися тими, в яких уже врахована
