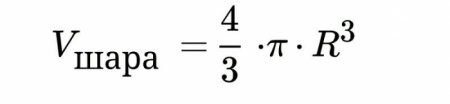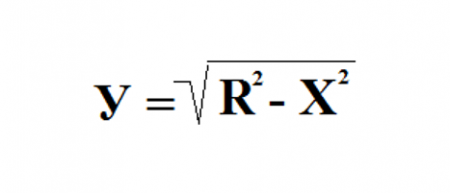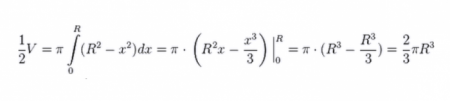Як обчислити об'єм кулі та інші нюанси при обчисленнях
Перш ніж почати вивчати поняття кулі, що таке об'єм кулі, розглядати формули обчислення його параметрів, необхідно згадати про поняття кола, досліджуваному раніше в курсі геометрії. Адже більшість дій в тривимірному просторі аналогічні або випливають з двовимірної геометрії з поправкою на появу третьої координати і третього ступеня.
Що таке коло?
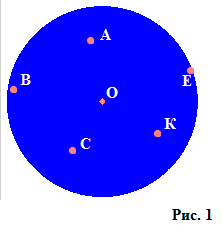 Коло – це фігура на декартовій площині (зображена на малюнку 1); найбільш часто визначення звучить як «геометричне місце всіх точок площини, відстань від яких до заданої точки (центру) не перевищує деякого ненегативного числа, званого радіусом». Як бачимо з малюнку, точка О – центр фігури, а безліч абсолютно всіх точок, що заповнюють коло, наприклад, А, В, С, К, Е, знаходяться не далі заданого радіусу (не виходять за межі кола, зображеної на рис. 2).
Коло – це фігура на декартовій площині (зображена на малюнку 1); найбільш часто визначення звучить як «геометричне місце всіх точок площини, відстань від яких до заданої точки (центру) не перевищує деякого ненегативного числа, званого радіусом». Як бачимо з малюнку, точка О – центр фігури, а безліч абсолютно всіх точок, що заповнюють коло, наприклад, А, В, С, К, Е, знаходяться не далі заданого радіусу (не виходять за межі кола, зображеної на рис. 2).  Якщо радіус дорівнює нулю, то коло перетворюється в точку.
Якщо радіус дорівнює нулю, то коло перетворюється в точку.
 Площа даних кіл обчислюється за такими формулами:
Площа даних кіл обчислюється за такими формулами: 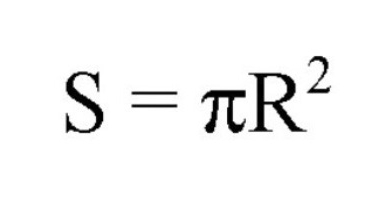
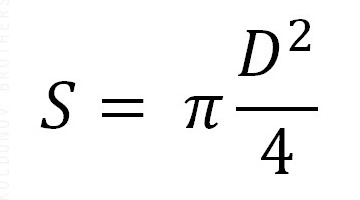 Тут S – це позначення площі, R – радіуса, D – діаметра. Також є константа, що дорівнює 314. Але не варто плутати, що для обчислення площі великого кола використовують радіус або діаметр самого кулі (сфери), а для визначення площі потрібні розміри радіусу саме малої окружності. Таких перерізів, які проходять через дві точки одного діаметра, що лежать на кордоні кулі, можна провести незліченну кількість. Як приклад – наша планета: дві точки на Північному і Південному полюсах, які є кінцями земної осі, а в геометричному сенсі – кінцями діаметра, і меридіани, які проходять через ці дві точки (малюнок 7). Тобто число великих кіл у сфери з кількістю прагне до нескінченності.
Тут S – це позначення площі, R – радіуса, D – діаметра. Також є константа, що дорівнює 314. Але не варто плутати, що для обчислення площі великого кола використовують радіус або діаметр самого кулі (сфери), а для визначення площі потрібні розміри радіусу саме малої окружності. Таких перерізів, які проходять через дві точки одного діаметра, що лежать на кордоні кулі, можна провести незліченну кількість. Як приклад – наша планета: дві точки на Північному і Південному полюсах, які є кінцями земної осі, а в геометричному сенсі – кінцями діаметра, і меридіани, які проходять через ці дві точки (малюнок 7). Тобто число великих кіл у сфери з кількістю прагне до нескінченності. 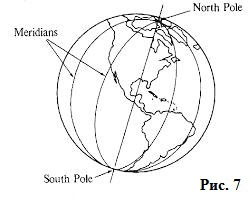
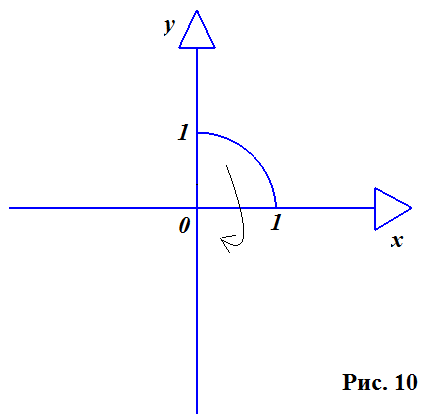 Беремо коло з одиничним радіусом і центром в початку координат. Рівняння такого кола виглядає наступним чином: Х 2 + У 2 = R 2 . Висловлюємо звідси У: У 2 = R 2 - Х 2 .
Беремо коло з одиничним радіусом і центром в початку координат. Рівняння такого кола виглядає наступним чином: Х 2 + У 2 = R 2 . Висловлюємо звідси У: У 2 = R 2 - Х 2 .
Обов'язково відзначимо, що отримана невід'ємна функція, безперервна і щербатий на відрізку Х (0; R), адже значення Х у тому випадку, коли ми розглядаємо чверть кола, лежить від нуля до значення радіуса, тобто до одиниці. Наступне, що ми робимо, це обертаємо нашу чверть кола навколо осі абсцис. В результаті ми отримаємо полушар. Щоб визначити його обсяг, вдамося до методів інтегрування.
Так як це обсяг лише напівкулі, збільшуємо результат в два рази, звідки одержуємо, що об'єм кулі дорівнює:
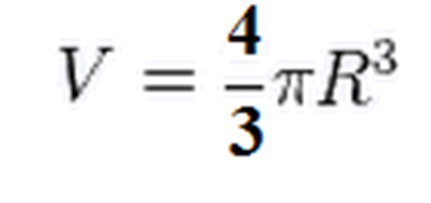
Що таке коло?


Проблеми з розумінням
Учні часто плутають ці поняття. Легко запам'ятати, провівши аналогію. Обруч, який діти крутять на уроках фізичної культури, – окружність. Розуміючи це або запам'ятавши, що перші літери обох слів – "О", діти мнемонічно будуть розуміти різницю.Введення поняття «куля»
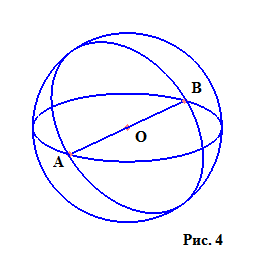
Куля – це тіло (рис. 3), обмежене якоюсь сферичною поверхнею. Що за «сферична поверхня», стане ясно з її визначення: це геометричне місце всіх точок на поверхні, відстань від яких до заданої точки (центру) не перевищує деякого ненегативного числа, званого радіусом. Як бачимо, поняття кола і сферичної поверхні аналогічні, тільки різняться простору, в яких вони знаходяться. Якщо зобразити кулю в двовимірному просторі, ми отримуємо коло, межею якого є коло (у кулі межа – сферична поверхня). На малюнку ми бачимо сферичну поверхню з радіусами ОА = ОВ.
Куля замкнутий і відкритий
У векторному та метричному просторі також розглядаються два поняття, пов'язані зі сферичною поверхнею. Якщо куля включає цю сферу в себе, то він називається замкнутим, а якщо ж ні, то в такому випадку куля є відкритим. Це більш "просунуті" поняття, їх вивчають у інститути при введенні в аналіз. Для простого, навіть побутового використання буде достатньо і тих формул, які вивчаються у курсі стереометрії 10-11 класів. Саме такі, доступні практично кожному середньостатистичному освіченій людині поняття будуть розглянуті далі.Поняття, які потрібно знати для наступних обчислень
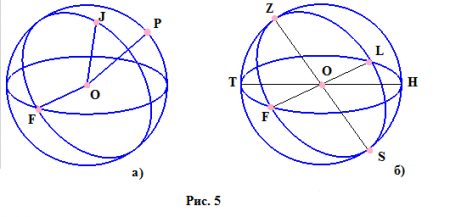
- Радіус і діаметр. - Радіус кулі і його діаметр визначаються так само, як у кола. - Радіус – відрізок, що з'єднує будь-яку точку на кордоні кулі і точку, яка є центром кулі. - Діаметр – відрізок, що з'єднує дві точки на кордоні кулі і проходить через його центр. Малюнок 5а наочно демонструє, які відрізки є радіусами кулі, а на малюнку 5б зображені діаметри сфери (відрізки, що проходять через точку О).Перерізу у сфері (кулі)
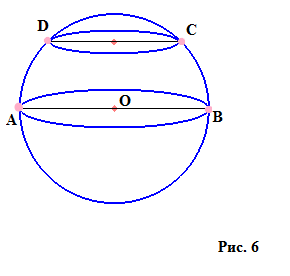
Будь-який перетин сфери є колом. Якщо воно проходить через центр кулі, називається великим кругом (коло з діаметром АВ), інші перерізу – малими колами (коло з діаметром DC).
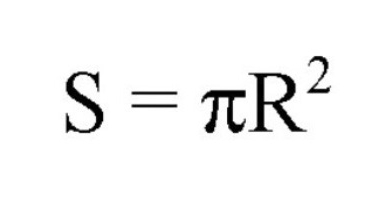
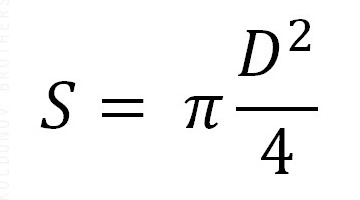

Частини кулі
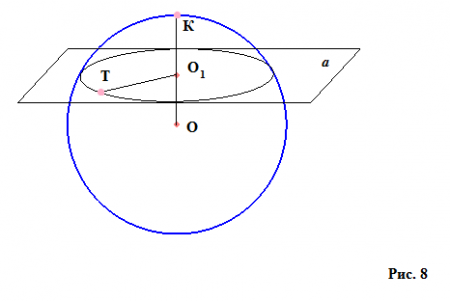
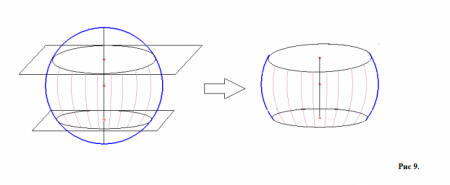
Якщо відсікти від сфери за допомогою деякої площини «шматочок» (малюнок 8), то він буде називатися сферичним або кульовим сегментом. У нього буде висота – перпендикуляр з центру січної площини до сферичної поверхні Про 1 К. Точка К на сферичній поверхні, в яку приходить висота, називається вершиною сферичного сегмента. А малий коло з радіусом Про 1 Т (в даному випадку, згідно з малюнком, площина не пройшла через центр сфери, але якщо перетин буде проходити через центр, то коло перетину буде великим), утворений при відсіканні кульового сегмента, буде називатися підставою нашого шматочка кулі – сферичного сегмента. Якщо з'єднати кожну точку підстави сферичного сегмента з центром сфери, ми отримаємо фігуру під назвою "кульовий сектор". Якщо через сферу проходять дві площини, які між собою паралельні, то та частина сфери, яка укладена між ними, називається кульовим шаром (малюнок 9 де зображена сфера з двома площинами і окремо – кульовий шар). Поверхня (виділена частина на малюнку 9 праворуч) цієї сфери називається поясом (знову для кращого розуміння можна провести аналогію з земною кулею, а саме з його кліматичними поясами – арктичними, тропічними, помірними і т. д.), а кола перетину будуть підставами кульового шару. Висота шару – частина діаметра, проведеного перпендикулярно до секущим площинах з центрів підстав. Існує також поняття кульової сфери. Вона утворюється в тому випадку, коли площини, які паралельні один одному, не перетинають сферу, а стосуються її в одній точці кожна.Формули для обчислення об'єму кулі і площі його поверхні
Куля утворюється при обертанні навколо нерухомого діаметра півкола або кола. Для обчислень різних параметрів даного об'єкта знадобиться не так вже й багато даних. Об'єм кулі, формула для обчислення якого вказано вище, виведений за допомогою інтегрування. Розберемося по пунктах. Розглядаємо коло у двомірній площині, адже, як було сказано вище, саме коло лежить в основі побудови кулі. Використовуємо лише його четверту частину (малюнок 10).
Обов'язково відзначимо, що отримана невід'ємна функція, безперервна і щербатий на відрізку Х (0; R), адже значення Х у тому випадку, коли ми розглядаємо чверть кола, лежить від нуля до значення радіуса, тобто до одиниці. Наступне, що ми робимо, це обертаємо нашу чверть кола навколо осі абсцис. В результаті ми отримаємо полушар. Щоб визначити його обсяг, вдамося до методів інтегрування.
Так як це обсяг лише напівкулі, збільшуємо результат в два рази, звідки одержуємо, що об'єм кулі дорівнює:
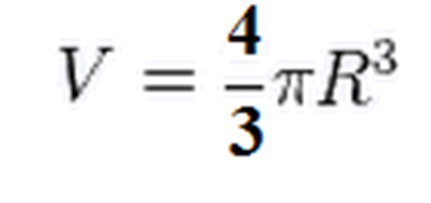
Дрібні нюанси
Якщо необхідно обчислити об'єм кулі через його діаметр, пам'ятаємо про те, що радіус – це половина діаметру, та підставляємо це значення в вищевказану формулу. Також до формули об'єму кулі можна дійти через площу його межує поверхні – сфери. Нагадаємо, що площа сфери обчислюється за формулою S = 4r 2 , проинтегрировав яку, також прийдемо до вищевказаної формули об'єму кулі. З цих формул можна виразити радіус, якщо в умові задачі є значення обсягу.Схожі добрі поради по темі

Що таке коло і круг, в чому їх відмінності та приклади фігур з життя
Шкільна пора для більшості дорослих людей асоціюється з безтурботним дитинством. Звичайно, багато неохоче відвідують школу, але тільки там вони
Як розрахувати довжину окружності і периметр кола?
Окружність зустрічається в повсякденному житті не рідше, ніж прямокутник. А у багатьох людей завдання про те, як розрахувати довжину окружності,
Як знайти радіус кола. Вписана і описана окружність
Радіус – це відрізок, що з'єднує будь-яку точку на колі з її центром. Це одна з найважливіших характеристик даної фігури, оскільки на її основі можна
Як знайти довжину окружності: через діаметр і радіус. Термінологія, основні формули та характеристика фігури
Окружність - замкнута крива, всі точки якої знаходяться на однаковій відстані від центру. Ця фігура є плоскою. Тому рішення задачі, питання якої
Новорічні кулі з паперу своїми руками
Тут насамперед доречно веномить про кулях з цигаркового паперу. Такі кулі різних кольорів дуже прикрашають ялинку. Кулі можна робити і з пап'є-маше в
Обертальний рух тіла. Закон обертального руху
У цій статті описується важливий розділ механіки - "Кінематика та динаміка обертального руху". Дані основні поняття і формули.