Обертальний рух тіла. Закон обертального руху
У цій статті описується важливий розділ фізики - "Кінематика та динаміка обертального руху".
Обертальний рух твердого тіла - це рух, при якому за концентричним (центри яких лежать на одній осі) кола рухаються всі точки тіла у відповідності з правилом для обертального руху матеріальної точки. Нехай довільне тверде тіло T здійснює обертання навколо осі O, яка перпендикулярна площині малюнка. Виберемо на даному тілі точку M. При обертанні ця точка буде описувати навколо осі O коло радіусом r .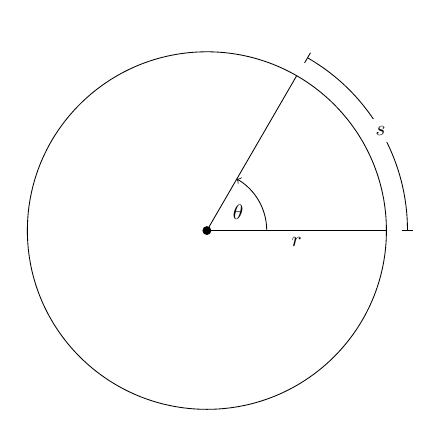 Через деякий час радіус повернеться щодо початкового положення на кут . За позитивний напрямок повороту прийнято напрямок правого гвинта (за годинниковою стрілкою). Зміна кута повороту з часом називається рівняння обертального руху твердого тіла: = (t). Якщо вимірювати в радіанах (1 рад - це кут, що відповідає дузі, довжиною дорівнює її радіусу), то довжина дуги кола S, яку пройде матеріальна точка M за час T, дорівнює: S = r.
Через деякий час радіус повернеться щодо початкового положення на кут . За позитивний напрямок повороту прийнято напрямок правого гвинта (за годинниковою стрілкою). Зміна кута повороту з часом називається рівняння обертального руху твердого тіла: = (t). Якщо вимірювати в радіанах (1 рад - це кут, що відповідає дузі, довжиною дорівнює її радіусу), то довжина дуги кола S, яку пройде матеріальна точка M за час T, дорівнює: S = r. 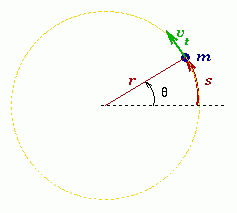 Кутова швидкість матеріальної точки або тіла - це фізична величина, яка визначається відношенням вектора елементарного повороту до тривалості цього повороту. Напрямок вектора можна визначити правилом правого гвинта уздовж осі О. В скалярному вигляді:
Кутова швидкість матеріальної точки або тіла - це фізична величина, яка визначається відношенням вектора елементарного повороту до тривалості цього повороту. Напрямок вектора можна визначити правилом правого гвинта уздовж осі О. В скалярному вигляді:
= d/dt. Якщо = d/dt = const, то такий рух називається рівномірний обертальний рух. При ньому кутову швидкість визначають за формулою = /t. Згідно попередньою формулою розмірність кутової швидкості [ω]= 1 рад/с. Рівномірний обертальний рух тіла можна описати періодом обертання. Період обертання T - фізична величина, що визначає час, за який тіло навколо осі обертання виконує один повний оборот ([T]= 1 с). Якщо у формулі для кутової швидкості прийняти t = T, = 2 (один повний оборот радіусу r), то = 2/T, тому період обертання визначимо наступним чином: T = 2/. Число оборотів, яке за одиницю часу здійснює тіло, називається частотою обертання , яка дорівнює: = 1/T. Одиниці виміру частоти: [ν]= 1/c = 1 c -1 = 1 Гц. Порівнюючи формули для кутової швидкості та частоти обертання, одержимо вираз, що пов'язує ці величини: = 2.
Вектор , що характеризує швидкість зміни кутової швидкості, називається вектором кутового прискорення: = d/dt.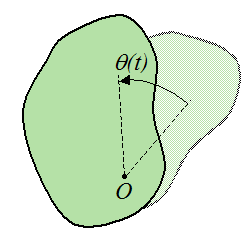 Якщо тіло обертається, прискорюючись, тобто d/dt > 0 вектор має напрямок уздовж осі в ту ж сторону, що і . Якщо обертальний рух уповільнено - d/dt < 0 , то вектори і протилежно спрямовані. Зауваження . Коли відбувається нерівномірний обертальний рух, вектор може змінюватися не тільки по величині, але і по напрямом (при повороті осі обертання).
Якщо тіло обертається, прискорюючись, тобто d/dt > 0 вектор має напрямок уздовж осі в ту ж сторону, що і . Якщо обертальний рух уповільнено - d/dt < 0 , то вектори і протилежно спрямовані. Зауваження . Коли відбувається нерівномірний обертальний рух, вектор може змінюватися не тільки по величині, але і по напрямом (при повороті осі обертання). 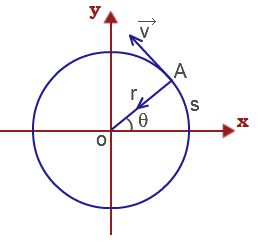 Нормальне прискорення матеріальної точки, що виконує обертально-поступальний рух, визначимо наступним чином: a = 2 /r = 2 r 2 /r. Отже, у скалярному вигляді a = 2 r. Тангенціальне прискореної матеріальної точки, яка виконує обертальний рух a = r.
Нормальне прискорення матеріальної точки, що виконує обертально-поступальний рух, визначимо наступним чином: a = 2 /r = 2 r 2 /r. Отже, у скалярному вигляді a = 2 r. Тангенціальне прискореної матеріальної точки, яка виконує обертальний рух a = r. 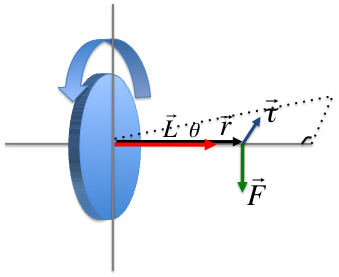 У скалярної формі L = m i i r i sin( i , r i ). Враховуючи, що при русі по колу радіус-вектор і вектор лінійної швидкості для i-ої матеріальної точки взаємно перпендикулярні, sin( i , r i ) = 1. Так що момент імпульсу матеріальної точки для обертального руху прийме вигляд L = m i i r i .
У скалярної формі L = m i i r i sin( i , r i ). Враховуючи, що при русі по колу радіус-вектор і вектор лінійної швидкості для i-ої матеріальної точки взаємно перпендикулярні, sin( i , r i ) = 1. Так що момент імпульсу матеріальної точки для обертального руху прийме вигляд L = m i i r i .
I = I 0 + ma 2 , де I 0 - початковий момент інерції тіла; m - маса тіла; a - відстань між осями.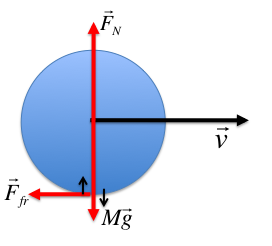 Якщо система, яка здійснює обертів округ нерухомої осі, складається з n тіл, то сумарний момент інерції такого типу системи дорівнює сумі моментів, її складових (закон додавання моментів інерції).
Якщо система, яка здійснює обертів округ нерухомої осі, складається з n тіл, то сумарний момент інерції такого типу системи дорівнює сумі моментів, її складових (закон додавання моментів інерції).
Основні поняття кінематики обертального руху
Обертальним рухом матеріальної точки навколо нерухомої осі називають такий рух, траєкторією якого є окружність, що знаходиться в площині перпендикулярній до осі, а центр її лежить на осі обертання.Обертальний рух твердого тіла - це рух, при якому за концентричним (центри яких лежать на одній осі) кола рухаються всі точки тіла у відповідності з правилом для обертального руху матеріальної точки. Нехай довільне тверде тіло T здійснює обертання навколо осі O, яка перпендикулярна площині малюнка. Виберемо на даному тілі точку M. При обертанні ця точка буде описувати навколо осі O коло радіусом r .

Основні елементи кінематики рівномірного обертального руху
Мірою переміщення матеріальної точки за невеликий проміжок часу dt служить вектор елементарного повороту d .
= d/dt. Якщо = d/dt = const, то такий рух називається рівномірний обертальний рух. При ньому кутову швидкість визначають за формулою = /t. Згідно попередньою формулою розмірність кутової швидкості [ω]= 1 рад/с. Рівномірний обертальний рух тіла можна описати періодом обертання. Період обертання T - фізична величина, що визначає час, за який тіло навколо осі обертання виконує один повний оборот ([T]= 1 с). Якщо у формулі для кутової швидкості прийняти t = T, = 2 (один повний оборот радіусу r), то = 2/T, тому період обертання визначимо наступним чином: T = 2/. Число оборотів, яке за одиницю часу здійснює тіло, називається частотою обертання , яка дорівнює: = 1/T. Одиниці виміру частоти: [ν]= 1/c = 1 c -1 = 1 Гц. Порівнюючи формули для кутової швидкості та частоти обертання, одержимо вираз, що пов'язує ці величини: = 2.
Основні елементи кінематики нерівномірного обертального руху
Нерівномірне обертальний рух твердого тіла або матеріальної точки навколо нерухомої осі характеризує його кутова швидкість, яка змінюється з часом.Вектор , що характеризує швидкість зміни кутової швидкості, називається вектором кутового прискорення: = d/dt.

Зв'язок величин, що характеризують поступальний і обертальний рух
Відомо, що довжина дуги з кутом повороту радіуса і його величиною пов'язана співвідношенням S = r. Тоді лінійна швидкість матеріальної точки, що виконує обертальний рух = S/t = r/t = r.
Момент імпульсу матеріальної точки
Векторний добуток радіус-вектора траєкторії матеріальної точки масою m i на її імпульс називається моментом імпульсу цієї точки відносно осі обертання. Напрямок вектора можна визначити, скориставшись правилом правого гвинта. Момент імпульсу матеріальної точки ( L i ) спрямований перпендикулярно площини, проведеної через r i і i , та утворює з ними праву трійку векторів (тобто при русі з кінця вектора r i до i правий гвинт покаже напрямок вектора L i ).
Момент сили, що діє на i-ю матеріальну точку
Векторний добуток радіус-вектора, який проведений у точку прикладання сили, на цю силу називається моментом сили, що діє на i-ю матеріальної точки відносно осі обертання. У скалярної формі M i = r i F i sin(r i , F i ). Вважаючи, що r i sin = l i , M i = l i F i . Величина l i , що дорівнює довжині перпендикуляра, опущеного з точки обертання на напрямок дії сили, називається плечем сили F i .Динаміка обертального руху
Рівняння динаміки обертального руху записується так: M = dL/dt. Формулювання закону наступна: швидкість зміни моменту імпульсу тіла, яке здійснює обертання навколо нерухомої осі, дорівнює результирующему моменту відносно цієї осі всіх зовнішніх сил, прикладених до тіла.Момент імпульсу і момент інерції
Відомо, що для i-ої матеріальної точки момент імпульсу в скалярної формі задається формулою L i = m i i r i . Якщо замість лінійної швидкості підставити її вираз через кутову: i = r i , то вираз для моменту імпульсу прийме вигляд L i = m i r i 2 . Величина I i = m i r i 2 називається моментом інерції щодо осі i-ої матеріальної точки, абсолютно твердого тіла, що проходить через його центр мас. Тоді момент імпульсу матеріальної точки запишемо: L i = I i . Момент імпульсу абсолютно твердого тіла запишемо суму моментів імпульсу матеріальних точок, що складають дане тіло: L = I.Момент сили і момент інерції
Закон обертального руху говорить: M = dL/dt. Відомо, що уявити момент імпульсу тіла можна через момент інерції: L = I. Тоді M = Id/dt. Враховуючи, що кутове прискорення визначається виразом = d/dt, отримаємо формулу для моменту сили, представленого через момент інерції: M = I. Зауваження. Момент сили вважається позитивним, якщо кутове прискорення, яким він викликаний, більше нуля, і навпаки.Теорема Штейнера. Закон додавання моментів інерції
Якщо вісь обертання тіла через його центр мас не проходить, то відносно цієї осі можна знайти його момент інерції за теоремою Штейнера:I = I 0 + ma 2 , де I 0 - початковий момент інерції тіла; m - маса тіла; a - відстань між осями.

Схожі добрі поради по темі
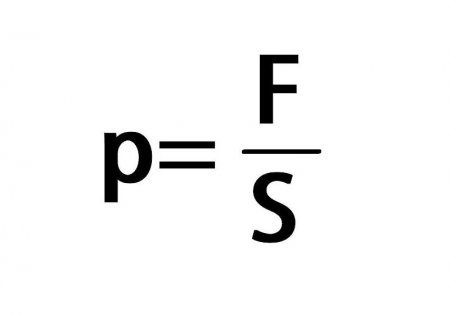
Основні формули з фізики за 9 клас. Все, що потрібно знати!
Основні формули з фізики, пояснення за формулами, шкільна програма та подальше навчання, допомога школяреві у вивченні фізики, практичне застосування

Основні поняття кінематики і рівняння
Що являють собою основні поняття кінематики? Що це взагалі за наука і вивченням чого вона займається? Сьогодні ми поговоримо про те, що являє собою
Кінематика - це Кінематика: визначення, формули, задачі
Що таке кінематика? Кінематика-це розділ механіки, який вивчає математичні і геометричні методи опису руху ідеалізованих об'єктів. Темою
Що таке кінематика? Розділ механіки, який вивчає математичний опис руху ідеалізованих тел
Що таке кінематика? З її визначенням вперше починають знайомитися учні середніх шкіл на уроках фізики. Механіка (кінематика є одним з її розділів)
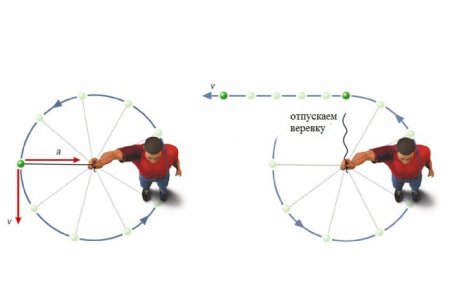
Доцентрове прискорення виведення формули і практичне застосування
Доцентровеприскорення супроводжує нас всюди. Саме воно змушує нашу Землю обертатися навколо Сонця. Виникаюча при цьому сила тяжіння дозволяє нам
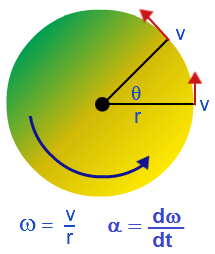
Обертальний рух і кутова швидкість твердого тіла
У цій статті мова піде про фізичних величинах, які характеризують обертальний рух тіла: кутова швидкість, кутове переміщення, кутове прискорення,
