Доцентрове прискорення виведення формули і практичне застосування
Доцентрове прискорення супроводжує нас всюди. Саме воно змушує нашу Землю обертатися навколо Сонця. Виникаюча при цьому сила тяжіння дозволяє нам існувати на цій планеті. Як можна зрозуміти, що являє собою Доцентрове прискорення? Визначення цієї фізичної величини представлено нижче.
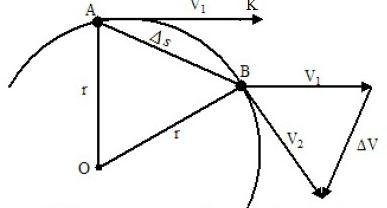 Якщо проміжок часу t взяти пренебрежимо малим, то дуга AB буде мало відрізнятися від хорди AB. Таким чином, можна замінити рух по дузі рухом по хорді. В цьому випадку переміщення каменю по хорді буде підкорятися законам прямолінійного руху, тобто пройдену відстань AB буде дорівнює добутку швидкості каменю на час його руху. AB = V х t. Позначимо шукане центростремительное прискорення буквою a. Тоді пройдений тільки під дією доцентрового прискорення шлях можна розрахувати за формулою равноускоренного руху: AO = at 2 /2. Відстань AB дорівнює добутку швидкості і часу, тобто AB = V х t, AO – раніше обчислено за формулою равноускоренного руху для переміщення по прямой: AO = at 2 /2. Підставляючи ці дані у формулу і перетворюючи їх, отримуємо просту і витончену формулу доцентрового прискорення: a = v 2 /R Словами це можна виразити так: центростремительное прискорення тіла, що рухається по колу, дорівнює частці від ділення лінійної швидкості в квадраті на радіус кола, по якій обертається тіло. Доцентрова сила в такому випадку буде виглядати так, як на картинці нижче.
Якщо проміжок часу t взяти пренебрежимо малим, то дуга AB буде мало відрізнятися від хорди AB. Таким чином, можна замінити рух по дузі рухом по хорді. В цьому випадку переміщення каменю по хорді буде підкорятися законам прямолінійного руху, тобто пройдену відстань AB буде дорівнює добутку швидкості каменю на час його руху. AB = V х t. Позначимо шукане центростремительное прискорення буквою a. Тоді пройдений тільки під дією доцентрового прискорення шлях можна розрахувати за формулою равноускоренного руху: AO = at 2 /2. Відстань AB дорівнює добутку швидкості і часу, тобто AB = V х t, AO – раніше обчислено за формулою равноускоренного руху для переміщення по прямой: AO = at 2 /2. Підставляючи ці дані у формулу і перетворюючи їх, отримуємо просту і витончену формулу доцентрового прискорення: a = v 2 /R Словами це можна виразити так: центростремительное прискорення тіла, що рухається по колу, дорівнює частці від ділення лінійної швидкості в квадраті на радіус кола, по якій обертається тіло. Доцентрова сила в такому випадку буде виглядати так, як на картинці нижче. 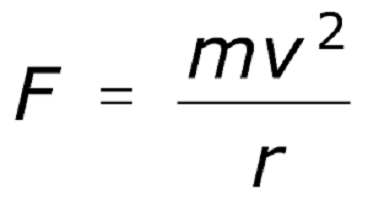
 Таким чином, можна зробити висновок про те, що прискорення не збільшує швидкість тіла, так як вектори швидкості та прискорення перпендикулярні один до одного. Додаючись до вектора швидкості, прискорення лише змінює напрям руху і утримує тіло на орбіті.
Таким чином, можна зробити висновок про те, що прискорення не збільшує швидкість тіла, так як вектори швидкості та прискорення перпендикулярні один до одного. Додаючись до вектора швидкості, прискорення лише змінює напрям руху і утримує тіло на орбіті.
 При діаметрі джутової мотузки близько 20 мм її міцність на розрив дорівнює близько 26 кН. Примітно, що довжина мотузки ніде не фігурує. Обертаючи вантаж розміром в 1 кг на мотузці радіусом до 1 м, можна вирахувати, що лінійна швидкість, необхідна для її розриву дорівнює 26 х 10 3 = 1кг х V 2 /1 м. Таким чином, швидкість, яку небезпечно перевищувати, буде дорівнює 26 х 10 3 = 161 м/с.
При діаметрі джутової мотузки близько 20 мм її міцність на розрив дорівнює близько 26 кН. Примітно, що довжина мотузки ніде не фігурує. Обертаючи вантаж розміром в 1 кг на мотузці радіусом до 1 м, можна вирахувати, що лінійна швидкість, необхідна для її розриву дорівнює 26 х 10 3 = 1кг х V 2 /1 м. Таким чином, швидкість, яку небезпечно перевищувати, буде дорівнює 26 х 10 3 = 161 м/с. 
Спостереження
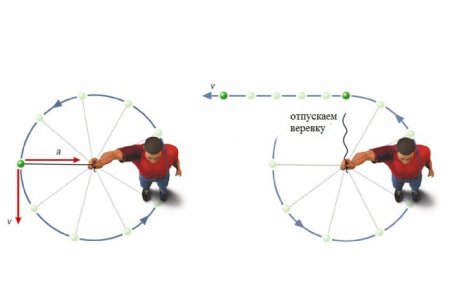
Найпростіший приклад прискорення тіла, що рухається по колу, можна спостерігати, обертаючи камінь на мотузці. Ви тягнете мотузку, а мотузка тягне камінь до центру. У кожен момент часу мотузка повідомляє каменю деяку кількість руху, і кожен раз – в новому напрямку. Можна уявити рух мотузки у вигляді серії слабких ривків. Ривок – і мотузка змінює свій напрямок, ще ривок – ще раз зміна, і так по колу. Якщо ви раптово відпустіть мотузку, ривки припиняться, а разом з ними і припиниться зміна напрямку швидкості. Камінь буде рухатися в напрямку дотичної до кола. Виникає питання: "З яким прискоренням буде рухатися тіло в цю мить?"Формула доцентрового прискорення
Насамперед варто зауважити, що рух тіла по колу є складним. Камінь бере участь у двох видах руху одночасно: під дією сили він рухається до центру обертання, і одночасно по дотичній до окружності, від цього центру видаляється. Згідно з Другим законом Ньютона, сила, що утримує камінь на мотузці, спрямована до центру обертання вздовж мотузки. Туди ж буде спрямований вектор прискорення. Нехай за деякий час t наш камінь, рівномірно рухаючись зі швидкістю V, потрапляє з точки A в точку B. Припустимо, що в момент часу, коли тіло перетинало точку B, на нього перестала діяти доцентрова сила. Тоді за проміжок часу воно потрапило б в точку K. Вона лежить на дотичній. Якщо б в той же момент часу на тіло діяли тільки доцентрові сили, то за час t, рухаючись з однаковим прискоренням, воно виявилося б в точці O, яка розташована на прямій, що представляє собою діаметр окружності. Обидва відрізка є векторами і підкоряються правилу векторного додавання. У результаті підсумовування цих двох рухів за відрізок часу t отримуємо результуючу руху по дузі AB.
Кутова швидкість
Кутова швидкість дорівнює частці від ділення лінійної швидкості на радіус кола. Вірно і зворотне твердження: V = R, де – кутова швидкість Якщо підставити це значення у формулу, можна отримати вираз відцентрового прискорення для кутової швидкості. Воно буде виглядати так: a = 2 R.Прискорення без зміни швидкості
І все ж, чому тіло з прискоренням, спрямованим до центру, не рухається швидше і не переміщається ближче до центру обертання? Відповідь криється в самому формулюванні прискорення. Факти говорять про те, що рух по колу реально, але для його підтримки потрібна прискорення, спрямоване до центру. Під дією сили, викликаної даними прискоренням, відбувається зміна кількості руху, в внаслідок чого траєкторія руху постійно викривляється, весь час змінюючи напрям вектора швидкості, але не змінюючи її абсолютної величини. Рухаючись по колу, наш багатостраждальний камінь спрямовується всередину, в іншому випадку він продовжував рухатися по дотичній. Кожну мить часу, йдучи по дотичній, камінь притягається до центру, але не влучає в нього. Ще одним прикладом доцентрового прискорення може стати водний лижник, що описує невеликі кола на воді. Фігура спортсмена нахилена; він ніби падає, продовжуючи рух і нахилившись вперед.
Перевищення запасу міцності
У попередньому досвіді ми мали справу з ідеальною мотузкою, яка не рвалася. Але, припустимо, наша мотузка звичайнісінька, і навіть можна обчислити зусилля, після якого вона просто порветься. Для того щоб розрахувати цю силу, досить зіставити запас міцності мотузки з навантаженням, яку вона відчуває в процесі обертання каменю. Обертаючи камінь з більшою швидкістю, ви повідомляєте йому більшу кількість руху, а значить, і більше прискорення.
Сила тяжіння
При розгляді досвіду ми нехтували дією сили тяжіння, так як при таких великих швидкостях її вплив пренебрежимо мало. Але можна помітити, що при розкручуванні довгої мотузки тіло описує більш складну траєкторію і поступово наближається до землі.Небесні тіла
Якщо перенести закони руху по колу в космос і застосувати їх до руху небесних тіл, можна заново відкрити кілька давно знайомих формул. Наприклад, сила, з якою тіло притягується до Землі, відома за формулою: F= m*g. У нашому випадку множник g і є тим самим доцентровим прискоренням, яке було виведено з попередньої формули. Тільки в цьому випадку роль каменю буде виконувати небесне тіло, притягивающееся до Землі, а роль мотузки – сила земного тяжіння. Множник g буде виражений через радіус нашої планети і швидкість її обертання.
Підсумки
Сутність доцентрового прискорення полягає у важкій і невдячній роботі утримання рухомого тіла на орбіті. Спостерігається парадоксальний випадок, коли при постійному прискоренні тіло не змінює величини своєї швидкості. Для непідготовленого розуму таку заяву досить парадоксально. Тим не менш і при розрахунку руху електрона навколо ядра, і при обчисленні швидкості обертання зірки навколо чорної діри, доцентрової прискорення відіграє не останню роль.Схожі добрі поради по темі

Шпагат джутовий: характеристики, застосування, поробки
Шпагат джутовий (мотузка) являє собою нитку натурального походження. Він виготовляється з джутового чагарнику, що вирощується в Африці, Азії, Америці
Яка величина є векторної, а яка скалярної? Просто про складне
Наведені приклади векторних і скалярних величин. Дано визначення цих величин. Стаття адресована школярам, які хочуть зрозуміти, що таке скаляр і
Рівноприскорений рух. Завдання і формули
Найважливішою характеристикою при русі тіла є його швидкість. Знаючи її, а також деякі інші параметри, ми завжди можемо визначити час руху, пройдену
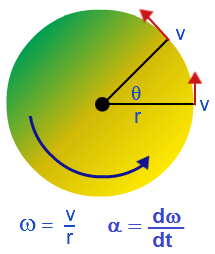
Обертальний рух і кутова швидкість твердого тіла
У цій статті мова піде про фізичних величинах, які характеризують обертальний рух тіла: кутова швидкість, кутове переміщення, кутове прискорення,

Що таке сила тяжіння і яке її значення для життя на Землі
Визначення сили тяжіння вперше було сформульовано Ісааком Ньютоном. Завдяки аналізу руху небесних тіл він зміг не тільки розповісти, чому планети не
Обертальний рух тіла. Закон обертального руху
У цій статті описується важливий розділ механіки - "Кінематика та динаміка обертального руху". Дані основні поняття і формули.