Векторна величина у фізиці. Приклади векторних величин
Фізика і математика, не обходяться без поняття «векторна величина». Її необхідно знати і дізнаватися, а також вміти з нею оперувати. Цього обов'язково варто навчитися, щоб не плутатися і не допускати дурних помилок.
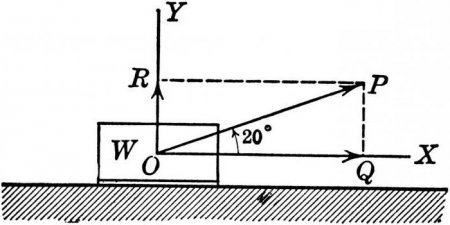
Векторна величина, крім числової величини, яка завжди береться за модулем, характеризується ще й напрямком. Тому вона може бути зображена графічно, тобто у вигляді стрілки, довжина якої дорівнює модулю величини, спрямованої в певну сторону. При листі кожна векторна величина позначається знаком стрілки на буквою. Якщо йдеться про числовому значенні, то стрілка не пишеться або її беруть за модулем.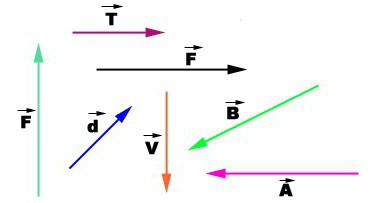
Правило паралелограма можна використовувати, коли потрібно скласти векторні величини в фізики. На відміну від першого правила, тут їх слід відкладати від однієї точки. Потім добудувати їх до паралелограма. Результатом дії слід вважати діагональ паралелограма, проведену з тієї ж точки. Якщо векторна величина віднімається з іншого, то вони знову відкладаються з однієї точки. Тільки результатом буде вектор, який збігається з тим, що відкладений від кінця до другого кінця першого.
Позначення у формулі
Найменування
v
швидкість
r
переміщення
а
прискорення
F
сила
р
імпульс
Е
напруженість електричного поля
У
магнітна індукція
М
момент сили
Тепер трохи докладніше про деяких з цих величин.
Цю ж формулу допустимо використовувати при нерівномірному русі. Тільки тоді вона буде середньої. Причому інтервал часу, який необхідно вибирати, обов'язково повинен бути як можна менше. При прагненні проміжку часу до нуля значення швидкості вже є миттєвим. Якщо розглядається довільне рух, то тут завжди швидкість — векторна величина. Адже її доводиться розкладати на складові, спрямовані вздовж кожного вектора, направляючого координатні прямі. До того ж він визначається як похідна радіус-вектора, узята по часу.
Сила
Точка докладання
Напрямок
тяжкості
центр тіла
до центру Землі
всесвітнього тяжіння
центр тіла
до центру іншого тіла
пружності
місце зіткнення взаємодіючих тіл
проти зовнішнього впливу
тертя
між дотичними поверхнями
в сторону, протилежну руху
Також ще векторною величиною є рівнодіюча сила. Вона визначається як сума всіх діючих на тіло механічних сил. Для її визначення необхідно виконати додавання за принципом правила трикутника. Тільки відкладати вектори потрібно по черзі від кінця попереднього. Результатом виявиться той, який сполучає початок першого з кінцем останнього.
Тут може постати таке питання: «Шлях — векторна величина?». В загальному випадку це твердження не є вірним. Шлях дорівнює довжині траєкторії і не має певного напряму. Винятком вважається ситуація, коли розглядається прямолінійний рух в одному напрямку. Тоді модуль вектора переміщення збігається за значенням з шляхом, і напрямок у них виявляється однаковим. Тому при розгляді руху вздовж прямої без зміни напрямку переміщення шлях можна включити в приклади векторних величин.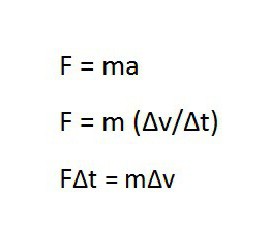
Як відрізнити скалярну величину від векторної?
Перша завжди має тільки одну характеристику. Це її числове значення. Більшість скалярних величин можуть приймати як позитивні, так і негативні значення. Їх прикладами може служити електричний заряд, робота або температура. Але є такі скаляри, які не можуть бути негативними, наприклад, довжина і маса.Векторна величина, крім числової величини, яка завжди береться за модулем, характеризується ще й напрямком. Тому вона може бути зображена графічно, тобто у вигляді стрілки, довжина якої дорівнює модулю величини, спрямованої в певну сторону. При листі кожна векторна величина позначається знаком стрілки на буквою. Якщо йдеться про числовому значенні, то стрілка не пишеться або її беруть за модулем.

Які дії найчастіше виконуються з векторами?
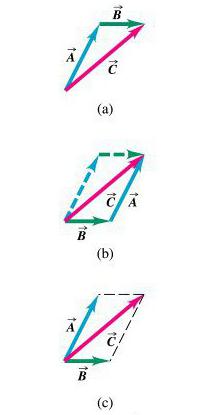
Спочатку — порівняння. Вони можуть бути рівними або немає. У першому випадку їх модулі однакові. Але це не єдина умова. У них повинні бути однакові або протилежні напрями. У першому випадку їх слід називати рівними векторами. У другому вони виявляються протилежними. Якщо не виконується хоча б одна із зазначених умов, то вектори не рівні. Потім йде додавання. Його можна зробити за двома правилами: трикутника або паралелограма. Перше наказує відкладати спочатку один вектор, потім від його кінця другий. Результатом складання буде той, який потрібно провести від початку першого до кінця другого.Правило паралелограма можна використовувати, коли потрібно скласти векторні величини в фізики. На відміну від першого правила, тут їх слід відкладати від однієї точки. Потім добудувати їх до паралелограма. Результатом дії слід вважати діагональ паралелограма, проведену з тієї ж точки. Якщо векторна величина віднімається з іншого, то вони знову відкладаються з однієї точки. Тільки результатом буде вектор, який збігається з тим, що відкладений від кінця до другого кінця першого.
Які вектори вивчають у фізиці?
Їх так само багато, як скаляров. Можна просто запам'ятати те, які векторні величини у фізиці існують. Або знати ознаки, за якими їх можна обчислити. Тим, хто віддає перевагу перший варіант, стане в нагоді така таблиця. В ній наведені основні векторні фізичні величини.Позначення у формулі
Найменування
v
швидкість
r
переміщення
а
прискорення
F
сила
р
імпульс
Е
напруженість електричного поля
У
магнітна індукція
М
момент сили
Тепер трохи докладніше про деяких з цих величин.
Перша величина — швидкість
З неї варто почати наводити приклади векторних величин. Це обумовлено тим, що її вивчають в числі перших. Швидкість визначається як характеристика руху тіла в просторі. Нею визначається числове значення і напрям. Тому швидкість є векторною величиною. До того ж її прийнято поділяти на види. Перший є лінійною швидкістю. Її вводять при розгляді прямолінійного рівномірного руху. При цьому вона виявляється дорівнює відношенню шляху, пройденого тілом, до часу руху.Цю ж формулу допустимо використовувати при нерівномірному русі. Тільки тоді вона буде середньої. Причому інтервал часу, який необхідно вибирати, обов'язково повинен бути як можна менше. При прагненні проміжку часу до нуля значення швидкості вже є миттєвим. Якщо розглядається довільне рух, то тут завжди швидкість — векторна величина. Адже її доводиться розкладати на складові, спрямовані вздовж кожного вектора, направляючого координатні прямі. До того ж він визначається як похідна радіус-вектора, узята по часу.
Друга величина — сила
Вона визначає міру інтенсивності впливу, що чиниться на тіло з боку інших тіл або полів. Оскільки сила — векторна величина, то вона обов'язково має своє значення по модулю і напрям. Так як вона діє на тіло, то важливим є ще й точка, до якої прикладена сила. Щоб отримати наочне уявлення про вектори сил, можна звернутися до наступної таблиці.Сила
Точка докладання
Напрямок
тяжкості
центр тіла
до центру Землі
всесвітнього тяжіння
центр тіла
до центру іншого тіла
пружності
місце зіткнення взаємодіючих тіл
проти зовнішнього впливу
тертя
між дотичними поверхнями
в сторону, протилежну руху
Також ще векторною величиною є рівнодіюча сила. Вона визначається як сума всіх діючих на тіло механічних сил. Для її визначення необхідно виконати додавання за принципом правила трикутника. Тільки відкладати вектори потрібно по черзі від кінця попереднього. Результатом виявиться той, який сполучає початок першого з кінцем останнього.
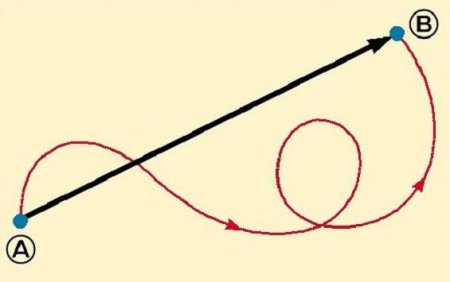
Третя величина переміщення
Під час руху тіло описує деяку лінію. Вона називається траєкторією. Ця лінія може бути абсолютно різною. Важливіше виявляється не її зовнішній вигляд, а точки початку і кінця руху. Вони з'єднуються відрізком, який називається переміщенням. Це теж векторна величина. Причому воно завжди спрямоване від початку переміщення до точки, де рух було припинено. Позначати його прийнято латинською літерою r.Тут може постати таке питання: «Шлях — векторна величина?». В загальному випадку це твердження не є вірним. Шлях дорівнює довжині траєкторії і не має певного напряму. Винятком вважається ситуація, коли розглядається прямолінійний рух в одному напрямку. Тоді модуль вектора переміщення збігається за значенням з шляхом, і напрямок у них виявляється однаковим. Тому при розгляді руху вздовж прямої без зміни напрямку переміщення шлях можна включити в приклади векторних величин.
Четверта величина — прискорення
Воно є характеристикою швидкості зміни швидкості. Причому прискорення може мати як позитивне, так і негативне значення. При прямолінійному русі воно спрямоване в бік більшої швидкості. Якщо переміщення відбувається по криволінійній траєкторії, то вектор його прискорення розкладається на дві складові, одна з яких направлена до центру кривизни по радіусу. Виділяють середню і миттєве значення прискорення. Перше слід розраховувати як відношення зміни швидкості за певний проміжок часу до цього часу. При прагненні розглянутого інтервалу часу до нуля говорять про миттєве прискорення.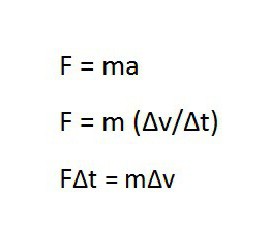
П'ята величина — імпульс
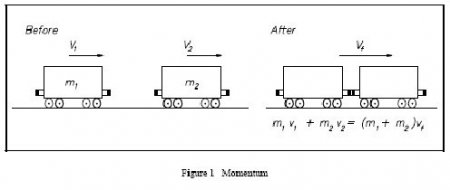
По-іншому його ще називають кількістю руху. Імпульс векторною величиною є з-за того, що безпосередньо пов'язаний зі швидкістю і силою, прикладеною до тіла. Обидві вони мають напрям і задають його імпульсу. За визначенням останній дорівнює добутку маси тіла на швидкість. Використовуючи поняття імпульсу тіла, можна по-іншому записати відомий закон Ньютона. Виходить, що зміна імпульсу дорівнює добутку сили на проміжок часу. У фізиці важливу роль має закон збереження імпульсу, який стверджує, що в замкненій системі тіл її сумарний імпульс є постійним. Ми дуже коротко перерахували, які величини (векторні) вивчаються в курсі фізики.Задача про непружному ударі
Умова. На рейках стоїть нерухома платформа. До неї наближається вагон зі швидкістю 4 м/с. Маси платформи та вагони - 10 і 40 тонн відповідно. Вагон вдаряється про платформу, відбувається автосцеп. Необхідно обчислити швидкість системи "вагон-платформа" після удару. Рішення. Спочатку потрібно ввести позначення: швидкість вагона до удару — v 1 , вагони з платформою після зчіпки — v, маса вагона m 1 , платформи — m 2 . За умовою задачі необхідно дізнатися значення швидкості v. Правила вирішення подібних завдань вимагають схематичного зображення системи до та після взаємодії. Вісь OX розумно направити уздовж рейок в ту сторону, куди рухається вагон. У даних умовах систему вагонів можна вважати замкненою. Це визначається тим, що зовнішніми силами можна знехтувати. Сила тяжіння і реакція опори врівноважені, а тертя об рейки не враховується. Відповідно до закону збереження імпульсу, їх векторна сума до взаємодії вагона і платформи дорівнює загальним для зчіпки після удару. Спочатку платформа не рухалася, тому її імпульс дорівнює нулю. Переміщувався тільки вагон, його імпульс — твір m 1 і v 1 . Так як удар непружний, тобто вагон зчепився з платформою, і далі почали котитися разом в ту ж сторону, то імпульс системи не змінив напрямку. Але його значення стало іншим. А саме твором суми маси вагона з платформою і потрібної швидкості. Можна записати таке рівняння: m 1 * v 1 = (m 1 + m 2 ) * v. Воно буде вірно для проекції векторів імпульсів на обрану вісь. З нього легко вивести рівність, яка буде потрібно для обчислення шуканої швидкості: v = m 1 * v 1 /(m 1 + m 2 ). За правилами слід перевести значення для маси з тонн в кілограми. Тому при підстановці їх у формулу слід спочатку помножити відомі величини на тисячу. Прості розрахунки дають число 075 м/с. Відповідь. Швидкість вагона з платформою дорівнює 075 м/с.
Завдання з поділом тіла на частини
Умова . Швидкість летить гранати 20 м/с. Вона розривається на два осколки. Маса першого 18 кг. Він продовжує рухатися в напрямку, в якому летіла граната, зі швидкістю 50 м/с. Другий осколок має масу 12 кг. Яка його швидкість? Рішення. Нехай маси осколків позначені літерами m 1 і m 2 . Їх швидкості відповідно будуть v 1 і v 2 . Початкова швидкість гранати — v. В задачі потрібно обчислити значення v 2 . Для того щоб більший осколок продовжував рухатися в тому ж напрямку, що і вся граната, другий повинен полетіти у зворотний бік. Якщо вибрати за напрям осі те, яке було у початкового імпульсу, то після розриву великий осколок летить по осі, а маленький — проти осі. У цій задачі дозволено користуватися законом збереження імпульсу із-за того, що розрив гранати відбувається миттєво. Тому, незважаючи на те що на гранату і її частині діє сила тяжіння, вона не встигає подіяти і змінити напрямок вектора імпульсу з його значенням по модулю. Сума векторних величин імпульсу після розриву гранати дорівнює тому, який був до нього. Якщо записати закон збереження імпульсу тіла в проекції на вісь OX, то він виглядатиме так: (m 1 + m 2 ) * v = m 1 * v 1 — m 2 * v 2 . З нього просто висловити шукану швидкість. Вона визначиться за формулою: v 2 = ((m 1 + m 2 ) * v — m 1 * v 1 ) /m 2 . Після підстановки числових значень і розрахунків виходить 25 м/с. Відповідь. Швидкість маленького шматка дорівнює 25 м/с.Задача про постріл під кутом
Умова. На платформі масою M встановлено знаряддя. З нього робиться постріл снарядом масою m. Він вилітає під кутом ? до горизонту зі швидкістю v (даної щодо землі). Потрібно дізнатися значення швидкості платформи після пострілу. Рішення. У цій задачі можна використовувати закон збереження імпульсу в проекції на вісь OX. Але тільки в тому випадку, коли проекції зовнішніх равнодействующих сил дорівнює нулю. За напрям осі OX потрібно вибрати ту сторону, куди полетить снаряд, і паралельно горизонтальній лінії. У цьому випадку проекції сил тяжіння і реакції опори на OX будуть дорівнюють нулю. Завдання буде вирішена в загальному вигляді, так як немає конкретних даних для відомих величин. Відповіддю в ній є формула. Імпульс системи до пострілу був дорівнює нулю, оскільки платформа і снаряд були нерухомі. Нехай шукана швидкість платформи буде позначена латинською буквою u. Тоді її імпульс після пострілу визначиться як добуток маси на проекцію швидкості. Так як платформа відкотиться назад (проти напрямку осі OX), то значення імпульсу буде зі знаком мінус. Імпульс снаряда — твір його маси на проекцію швидкості на вісь OX. З-за того, що швидкість спрямована під кутом до горизонту, її проекція дорівнює швидкості, помноженій на косинус кута. У буквеному рівність це буде виглядати так: 0 = - Mu + mv * cos ?. З неї шляхом нескладних перетворень виходить формула-відповідь: u = (mv * cos ?) /M. Відповідь. Швидкість платформи визначається за формулою u = (mv * cos ?) /M.
Задача про переправу через річку
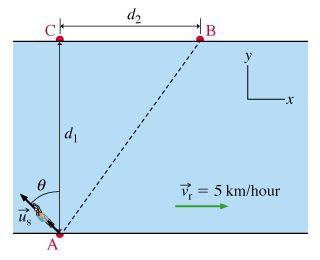
Умова. Ширина річки по всій її довжині однакове і дорівнює l, її береги паралельні. Відома швидкість течії води в річці v 1 і власна швидкість катера v 2 . 1). При переправі ніс катери спрямований строго до протилежного берега. На яку відстань s його знесе вниз за течією? 2). Під яким кутом ? потрібно направити ніс катери, щоб він досяг протилежного берега строго перпендикулярно до точки відправлення? Скільки часу t буде потрібно на таку переправу? Рішення. 1). Повна швидкість катера є векторною сумою двох величин. Перша з них протягом річки, яке направлене вздовж берегів. Друга — власна швидкість катера, перпендикулярна берегів. На кресленні виходить два подібних трикутника. Перший утворений шириною річки і відстанню, на яке зносить катер. Другий — векторами швидкостей. З них випливає такий запис: s /l = v 1 /v 2 . Після перетворення виходить формула для шуканої величини: s = l * (v 1 /v 2 ). 2). У цьому варіанті завдання вектор повній швидкості перпендикулярний берегів. Він дорівнює векторній сумі v 1 і v 2 . Синус кута, на який повинен відхилятися вектор власної швидкості, рівний відношенню модулів v 1 і v 2 . Для розрахунку часу руху потрібно розділити ширину річки на сосчитанную повну швидкість. Значення останньої обчислюється за теоремою Піфагора. v = ?(v 2 2 – v 1 2 ), тоді t = l /(?(v 2 2 – v 1 2 )). Відповідь. 1). s = l * (v 1 /v 2 ), 2). sin ? = v 1 /v 2 , t = l /(?(v 2 2 – v 1 2 )).Схожі добрі поради по темі

Закон Клапейрона-Менделєєва: формула, формулювання, використання
Кожен школяр, який навчається у десятому класі на одному з уроків фізики стикається з законом Клапейрона-Менделєєва, вивчає формули, формулювання,
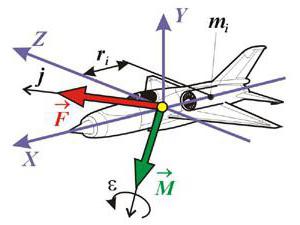
Яка величина є векторної, а яка скалярної? Просто про складне
Наведені приклади векторних і скалярних величин. Дано визначення цих величин. Стаття адресована школярам, які хочуть зрозуміти, що таке скаляр і
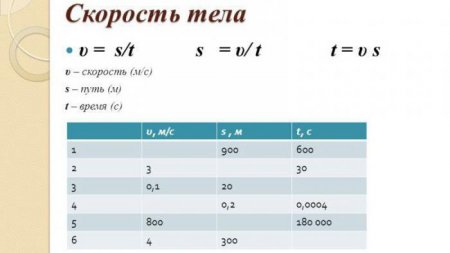
Як знайти швидкість. Поняття про фізичну величину і формула
Зважаючи на те, що така фізична величина, як швидкість, фігурує в багатьох задачах, що мають зв'язок з розділами механіки (а саме кінематикою і
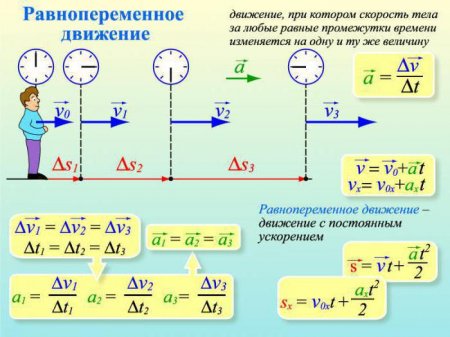
Рівноприскорений рух. Завдання і формули
Найважливішою характеристикою при русі тіла є його швидкість. Знаючи її, а також деякі інші параметри, ми завжди можемо визначити час руху, пройдену
Ділення на нуль. Захоплююча математика
Чому неможливо ділення на нуль, чим пояснити цей принцип елементарної математики? Як обходять цей принцип при вирішенні меж послідовностей?
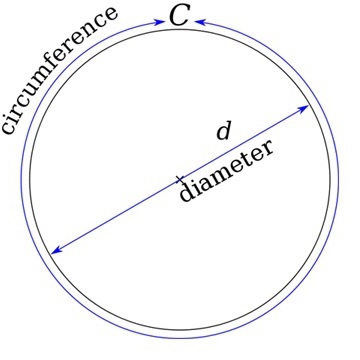
Як розрахувати довжину окружності і периметр кола?
Окружність зустрічається в повсякденному житті не рідше, ніж прямокутник. А у багатьох людей завдання про те, як розрахувати довжину окружності,