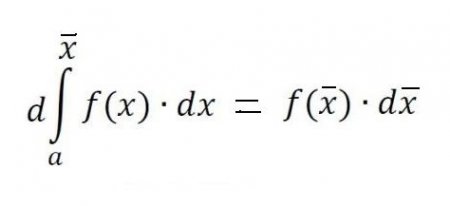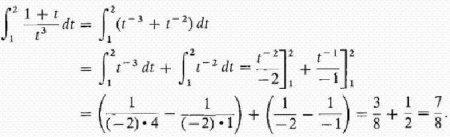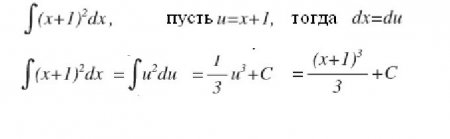Що таке інтеграл? Інтеграли з докладним рішенням. Таблиця інтегралів
Слово «інтеграл» походить від латинського integralis – цілісний. Цю назву запропонував у 17 ст. учень великого Лейбніца (і також видатний математик) В. Бернуллі. А що таке інтеграл в сучасному розумінні? Нижче ми постараємося дати всебічний відповідь на це питання.
Спочатку з розгляду таких залежностей фізичних величин, наприклад, шляху від швидкості, було сформовано математичне поняття функції y = f(x). Дослідження властивостей різних функцій призвело до зародження математичного аналізу. Вчені активно шукали способи вивчення властивостей різних функцій.
Геній Лейбніца і Ньютона в середині 17 ст. були створені методи, що дозволили вирішувати обидві ці завдання. Виявилося, що для проведення дотичної до кривої в точці потрібно знайти величину так званої похідною від функції, що описує криву, у розглянутій її точці, і ця величина виявляється рівною швидкості зміни функції, тобто стосовно до залежності «шлях від швидкості» власне миттєвою швидкістю тіла. Для знаходження же площі, обмеженої кривою лінією, слід обчислити визначений інтеграл, який давав її точну величину. Похідна та інтеграл – основні поняття диференціального і інтегрального числення, є базисом сучасного матаналізу – найважливішого розділу вищої математики.
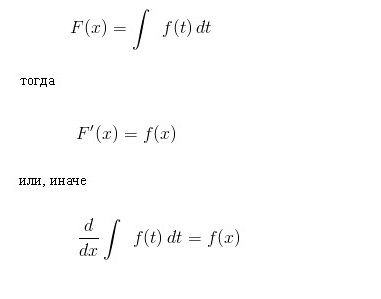 Як видно, при символі інтеграла відсутні межі інтегрування. Це означає, що з певного він перетворений на невизначений інтеграл. Слово «невизначений» означає, що результатом операції інтегрування в даному випадку є не одна, а безліч функцій. Адже, крім власне функції F(x), останнім виразами задовольняє і будь-яка функція F(x)+С, де С = const. При цьому мається на увазі, що постійний член в ансамблі первісних можна задавати по свавіллю. Слід підкреслити, що, якщо інтеграл, визначений від функції, є числом, то невизначений є функція, точніше, їх безліч. Термін «інтеграція» застосовується для визначення операції розвідки обох видів інтегралів.
Як видно, при символі інтеграла відсутні межі інтегрування. Це означає, що з певного він перетворений на невизначений інтеграл. Слово «невизначений» означає, що результатом операції інтегрування в даному випадку є не одна, а безліч функцій. Адже, крім власне функції F(x), останнім виразами задовольняє і будь-яка функція F(x)+С, де С = const. При цьому мається на увазі, що постійний член в ансамблі первісних можна задавати по свавіллю. Слід підкреслити, що, якщо інтеграл, визначений від функції, є числом, то невизначений є функція, точніше, їх безліч. Термін «інтеграція» застосовується для визначення операції розвідки обох видів інтегралів.
Історичні передумови виникнення поняття інтеграла
На початку 17 ст. у розгляді провідних вчених знаходилося велике число фізичних (перш всього механічних) завдань, в яких потрібно було дослідити залежність одних величин від інших. Найбільш наочними і нагальними проблемами були визначення миттєвої швидкості нерівномірного руху тіла в будь-який момент часу і зворотний цій задача знаходження величини шляху, пройденого тілом за певний проміжок часу при такому русі. Сьогодні ми вже знаємо, що таке інтеграл від швидкості руху – це і є пройдений шлях. Але розуміння того, як його обчислювати, знаючи швидкість кожен момент часу, з'явилося не відразу.Спочатку з розгляду таких залежностей фізичних величин, наприклад, шляху від швидкості, було сформовано математичне поняття функції y = f(x). Дослідження властивостей різних функцій призвело до зародження математичного аналізу. Вчені активно шукали способи вивчення властивостей різних функцій.
Як виникло обчислення інтегралів і похідних?
Після створення Декартом основ аналітичної геометрії і появи можливості зображати функціональні залежності графічно в осях декартової системи координат, перед дослідниками постали дві великі нові завдання: як провести дотичну до кривої лінії в будь-якій її точці і як знайти площу фігури, обмеженої зверху цією кривою і прямими, паралельними осям координат. Несподіваним чином виявилося, що перша з них еквівалентна знаходженню миттєвої швидкості, а друга – знаходження пройденого шляху. Адже він при нерівномірному рух зображувався у декартових осях координат «відстань» і «час» деякою кривою лінією.Геній Лейбніца і Ньютона в середині 17 ст. були створені методи, що дозволили вирішувати обидві ці завдання. Виявилося, що для проведення дотичної до кривої в точці потрібно знайти величину так званої похідною від функції, що описує криву, у розглянутій її точці, і ця величина виявляється рівною швидкості зміни функції, тобто стосовно до залежності «шлях від швидкості» власне миттєвою швидкістю тіла. Для знаходження же площі, обмеженої кривою лінією, слід обчислити визначений інтеграл, який давав її точну величину. Похідна та інтеграл – основні поняття диференціального і інтегрального числення, є базисом сучасного матаналізу – найважливішого розділу вищої математики.
Площа під кривою лінією
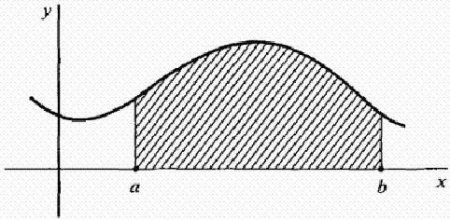
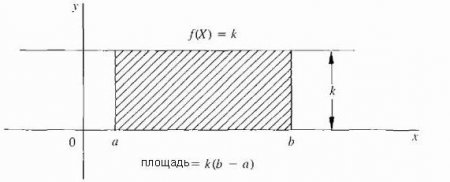
Отже, як же визначити її точну величину? Спробуємо розкрити процес її обчислення через інтеграл докладно, з самих азів. Нехай f є неперервною на відрізку[ab]функцією. Розглянемо криву y = f(x), зображену на малюнку нижче. Як знайти площу області, обмеженої кривої ), віссю х, і лініями х = а і х = b? Тобто площа заштрихованої фігури на малюнку. Самий простий випадок, коли f є постійною функцією; тобто, крива є горизонтальна лінія f(X) = k, де k-постійна і k >= 0 як показано на малюнку нижче. В цьому випадку область під кривою - всього лише прямокутник з висотою k і шириною (b – a), так що площа визначається як: k · (b - а). Області деяких інших простих фігур, таких як трикутник, трапеція і півколо, даються формулами з планіметрії. Площа під будь безперервної кривої у = f(х) дається визначеним інтегралом, який записується так само, як звичайний інтеграл.Риманова сума
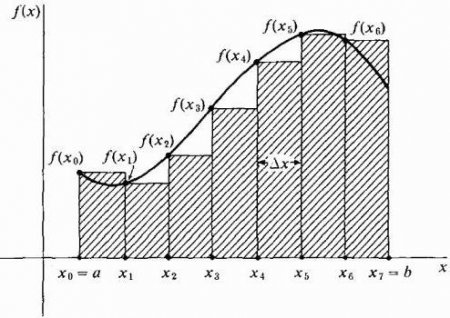
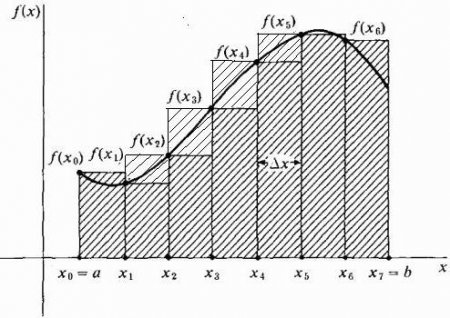
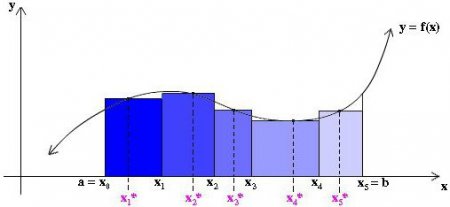
Перш ніж зануритися в докладний відповідь на питання, що таке інтеграл, виділимо деякі основні ідеї. По-перше, область під кривою ділиться на деяке число n вертикальних смуг досить малої ширини x. Далі кожна вертикальна смуга замінюється вертикальним прямокутником висотою f(х), шириною x, і площею f(х)dx. Наступним кроком є формування суми площ всіх цих прямокутників, званої Ріманової сумою (дивіться малюнки нижче). Малюючи наші прямокутники шириною x, ми можемо брати їх висоту, рівну значенню функції на лівому краю кожної смужки, тобто на кривій будуть лежати крайні ліві точки їх верхніх коротких сторін шириною x. При цьому на ділянці, де функція зростає, і її крива є опуклою, всі прямокутники виявляються нижче цієї кривої, тобто їх сума буде свідомо меншої точної величини площі під кривою на цій ділянці (см. малюнок нижче). Такий спосіб апроксимації називається лівостороннім. В принципі, можна намалювати апроксимуючі прямокутники таким чином, щоб на кривій лежали крайні праві точки їх верхніх коротких сторін шириною x. Тоді вони будуть вище кривої, і наближення площі на цій ділянці виявиться більше її точної величини, як показано на малюнку нижче. Цей спосіб зветься правостороннього. Але ми можемо також взяти висоту кожного з апроксимуючих прямокутників, рівній просто деякому значенню функції в довільній точці x* i всередині відповідної смужки x i (дивись рис. нижче). При цьому ми навіть можемо не брати однакову ширину всіх смужок. Складемо Риманову суму:Перехід від Ріманової суми до визначеного інтегралу
У вищій математиці доводиться теорема, яка говорить, що якщо при необмеженому зростанні числа n апроксимуючих прямокутників найбільша їх ширина прагне до нуля, то Риманова сума A n прагне до деякого межі A. Число A – одне і те ж при будь-якому способі освіти апроксимуючих прямокутників і при будь-якому виборі точок x* i . Наочне пояснення теорема дає малюнок нижче. З нього видно, що, чим вже прямокутники, тим ближче площу ступінчатої фігури до площі під кривою. При числі прямокутників n-> їх ширина x i ->0 а межа A суми A n чисельно дорівнює шуканої площі. Ця межа і є певний інтеграл функції f (х): Символ інтеграла, який представляє собою видозмінену курсивную літеру S, був введений Лейбніцем. Ставити зверху і знизу позначення інтеграла його межі запропонував Ж. Б. Фур'є. При цьому ясно вказується початкове і кінцеве значення x.Геометричний і механічний тлумачення певного інтеграла
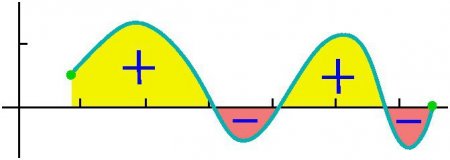
Спробуємо дати розгорнуту відповідь на питання про те, що таке інтеграл? Розглянемо інтеграл на відрізку[a,b]від позитивної всередині нього функції f(х), причому вважаємо, що верхня межа більше нижнього a всередині[a,b], то абсолютне значення інтеграла дорівнює площі між віссю абсцис і графіком y=f(х), сам же інтеграл від'ємний. У випадку однократного або неодноразового перетину графіка y=f(х) осі абсцис на відрізку[a,b]як показано на малюнку нижче, для обчислення інтеграла треба визначити різниця, в якій уменьшаемое буде дорівнює сумарній площі ділянок, що перебувають над віссю абсцис, а від'ємник – сумарної площі ділянок, що знаходяться під ній. Так, для функції, показаної на малюнку вище, визначений інтеграл від a до b дорівнює (S1 + S3) – (S2+S4). Механічне тлумачення певного інтеграла тісно пов'язане з геометричним. Повернемося до розділу «Риманова сума» і уявимо, що наведений на рисунках графік виражає функцію швидкості v=f(t) при нерівномірному русі матеріальної точки (вісь абсцис є віссю часу). Тоді площа будь-якого апроксимуючого прямокутника шириною t, який ми будували при формуванні Ріманової суми, буде висловлювати наближено шлях точки за час t, а саме v(t*)t. Повна сума площ прямокутників на відрізку від t 1 =a t 2 =b висловить наближено шлях s за час t 2 – t 1 , а межа її, тобто інтеграл (певний) від a до b функції v = f(t) dt дасть точне значення шляхи s.Диференціал визначеного інтеграла
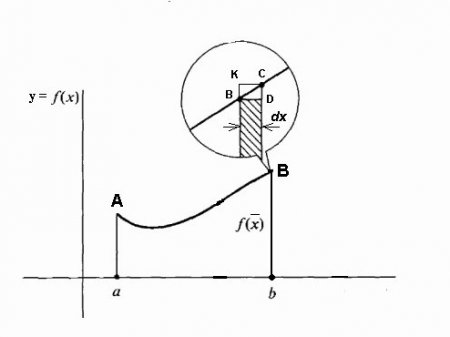
Якщо повернутися до його позначення, то цілком можна припустити, що a = const, а b є конкретним значенням деякої незалежної змінної x. Тоді визначений інтеграл з верхньою межею x з конкретного числа перетворюється у функцію від x. Такий інтеграл рівний площі фігури під кривою, позначеної точками aABb на малюнку нижче. При нерухомої лінії aA і рухомий Bb ця площа стає функцією f(x), причому приросту x раніше відкладаються уздовж осі х, а приростом функції f(x) є збільшення площі під кривою. Припустимо, що ми дали змінної x = b деяке мале прирощення x. Тоді збільшення площі фігури aABb складається з площі прямокутника (заштрихований на малюнку) Bb•x і площі фігури BDC під кривою. Площа прямокутника дорівнює Bb•x = f(x)x, тобто вона є лінійною функцією приросту незалежної змінної. Площа фігури BDC свідомо менше, ніж площа прямокутника BDCK = x•y, і при прагненні x ->0 вона зменшується ще швидше за нього. Значить, f(x)x = f(x)dx є диференціал змінної площі aABb, тобто диференціал визначеного інтеграла Звідси можна укласти, що обчислення інтегралів полягає в разискании функцій за заданими виразами їх диференціалів. Інтегральне числення як раз і являє собою систему способів розвідки таких функцій за відомими їх дифференциалам.Фундаментальне співвідношення інтегрального обчислення
Воно пов'язує відносини між диференціюванням та інтегруванням і показує, що існує операція, зворотна диференціювання функції, - її інтегрування. Воно також показує, що якщо будь-яка функція f(х) неперервна, то застосуванням до неї цієї математичної операції можна знайти цілий ансамбль (сукупність, множина) функцій, первісних для неї (або інакше, знайти невизначений інтеграл від неї). Нехай функція F(x) є позначенням результату інтегрування функції f(х). Відповідність між цими двома функціями в результаті інтегрування другий з них позначається наступним чином: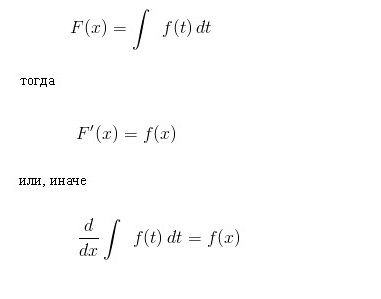
Основне правило інтегрування
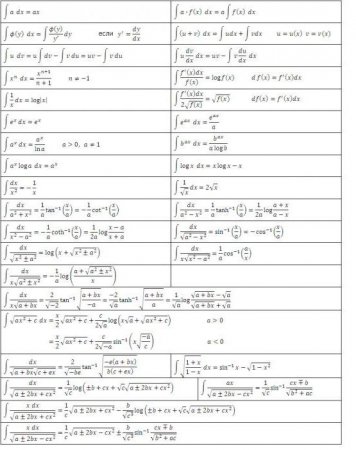
Воно являє собою повну протилежність відповідним правилом для диференціювання. Як же беруться невизначені інтеграли? Приклади цієї процедури ми розглянемо на конкретних функціях. Давайте подивимося на ступеневу функцію загального виду: f(х) = cx n Після того як ми зробили це з кожним доданком у вираженні інтегрується функції (якщо їх декілька), ми додаємо постійну наприкінці. Нагадаємо, що взяття похідної від постійної величини знищує її, тому взяття інтеграла від функції дасть нам відновлення цієї постійної. Ми позначаємо її, так як постійна невідома - це може бути будь-яке число! Тому ми можемо мати нескінченно багато виразів для невизначеного інтеграла. Давайте розглянемо прості невизначені інтеграли, приклади взяття яких показані нижче. Нехай потрібно знайти інтеграл від функції: f(х) = 4x 2 + 2x – 3. Почнемо з першого доданку. Ми дивимося на показник ступеня 2 і збільшуємо на 1 потім ділимо перший член на результуючий показник 3. Отримуємо: 4(x 3 ) /3. Потім ми дивимося на наступний член і робимо те ж саме. Так як він має показник ступеня 1 то результуючий показник буде 2. Таким чином, ми розділимо це доданок на 2: 2(x 2 ) /2 = x 2 . Останній член має множник х, але ми просто не бачимо його. Ми можемо уявити собі останній доданок як (-3x 0 ). Це еквівалентно (-3)•(1). Якщо ми використовуємо правило інтегрування, ми додамо 1 до показника, щоб підняти його до першого ступеня, а потім розділимо останній член на 1. Отримаємо 3x. Це правило інтегрування працює для всіх значень n, крім n = – 1 (тому що ми не можемо розділити на 0). Ми розглянули найбільш простий приклад знаходження інтеграла. Взагалі ж рішення інтегралів є справою непростою, і в ньому гарною підмогою є вже накопичений в математиці досвід.Таблиці інтегралів
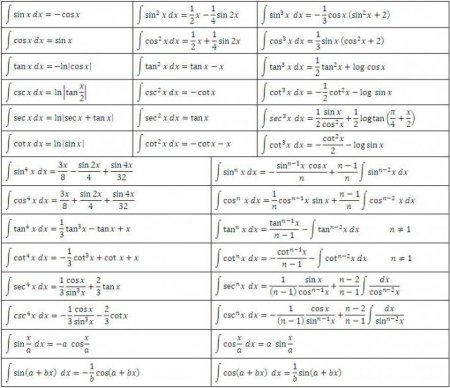
У розділі вище ми бачили, що з кожної формули диференціювання виходить відповідна формула інтегрування. Тому всі можливі їх варіанти вже давно отримані і зведені у відповідні таблиці. Наведена нижче таблиця інтегралів містить формули інтегрування основних алгебраїчних функцій. Ці формули потрібно знати на пам'ять, вивчаючи їх поступово, по мірі їх закріплення вправами. Ще одна таблиця інтегралів містить основні тригонометричні функції:Як же обчислити визначений інтеграл
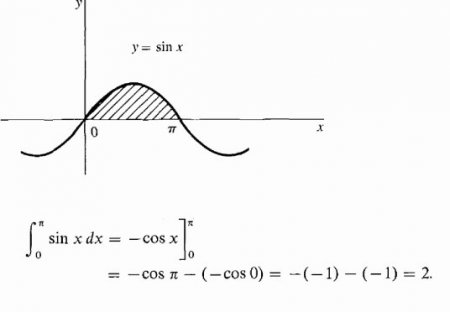
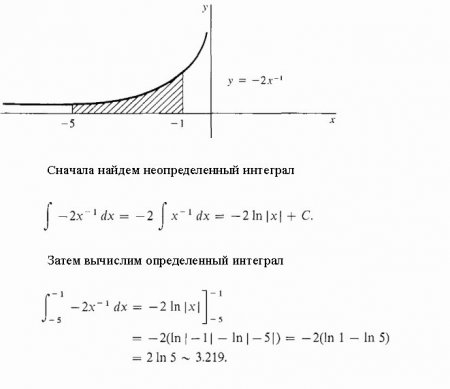
Виявляється, зробити це, вміючи інтегрувати, тобто знаходити невизначені інтеграли, дуже просто. І допомагає в цьому формула засновників інтегро-диференціального числення Ньютона і Лейбніца Згідно їй, обчислення шуканого інтеграла полягає на першому етапі в знаходженні невизначеного, подальшому обчисленні значення знайденої первісної F(x) при підстановці x, рівного спочатку верхньої межі, потім нижньому і, нарешті, у визначенні різниці цих значень. При цьому константу С можна не записувати. т. до. вона зникає при виконанні віднімання. Розглянемо деякі інтеграли з докладним рішенням. Знайдемо площу ділянки під однією полуволной синусоїдою. Обчислимо заштрихованную площа під гіперболою. Розглянемо тепер інтеграли з докладним рішенням , використовують у першому прикладі властивість адитивності, а в другому - підстановку проміжної змінної інтегрування. Обчислимо визначений інтеграл від дробово-раціональної функції: y=(1+t)/t 3 від t=1 до t=2. Тепер покажемо, як можна спростити взяття інтеграла введенням проміжної змінної. Нехай потрібно обчислити інтеграл від (x+1) 2 .Про невласних интегралах
Ми говорили про визначеному інтегралі для кінцевого проміжку[a,b]від безперервної на ньому функції f(х). Але ряд конкретних завдань призводить до необхідності розширити поняття інтеграла на випадок, коли межі (один або обидва) дорівнюють нескінченності, або при розривної функції. Наприклад, при обчисленні площ під кривими, асимптотично наближаються до осей координат. Для поширення поняття інтеграла на цей випадок, крім граничного переходу при обчисленні Ріманової суми апроксимуючих прямокутників, виконується ще один. При такому двократному переході до межі виходить невласний інтеграл. В протилежність йому всі інтеграли, про яких говорилося вище, називаються власними.Схожі добрі поради по темі

Парадокси Зенона Елейского - опис, значення та цікаві факти
Парадокси Зенона вводили в подив багатьох вчених і філософів до 17 століття. І до цих пір багато хто вчені сперечаються про нескінченності, структуру

Група «Інтеграл». Початок
Група «Інтеграл» утворилася в 1962 році. Її засновниками стали учні восьмого класу загальноосвітньої школи міста Чарска, що розташований в

Адіабатний процес, його суть та формули
Адіабатний процес (в деяких джерелах згадується як адіабатичний) - це термодинамічний процес, що відбувається при відсутності теплообміну з
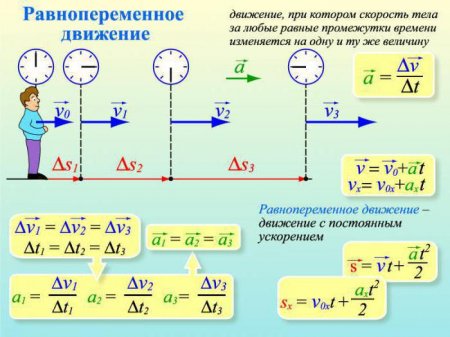
Рівноприскорений рух. Завдання і формули
Найважливішою характеристикою при русі тіла є його швидкість. Знаючи її, а також деякі інші параметри, ми завжди можемо визначити час руху, пройдену
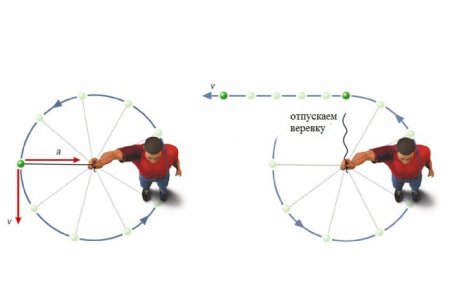
Доцентрове прискорення виведення формули і практичне застосування
Доцентровеприскорення супроводжує нас всюди. Саме воно змушує нашу Землю обертатися навколо Сонця. Виникаюча при цьому сила тяжіння дозволяє нам

Як знайти середню швидкість. Покрокова інструкція
Є середні величини, неправильне визначення яких увійшло у анекдот або притчу.У кожного, приміром, викличе посмішку саркастичного розуміння фраза