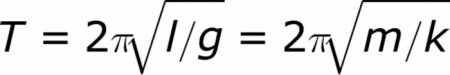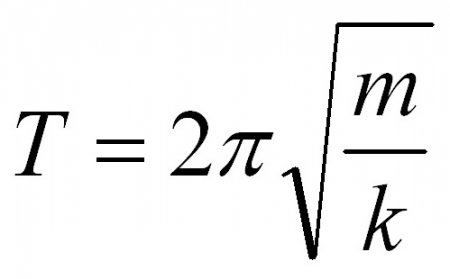Період коливань: досліди, формули, задачі
Що таке період коливань? Що це за величина, який фізичний сенс вона має і як її розрахувати? У цій статті ми розберемося з цими питаннями, розглянемо різні формули, за якими можна розрахувати період коливань, а також з'ясуємо, який зв'язок є між такими фізичними величинами, як період і частота коливань тіла/системи.
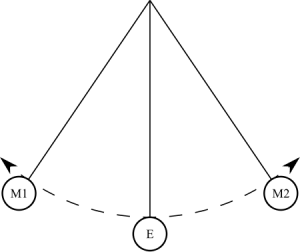 Отже, якщо вивести таку систему з рівноваги, прикласти до кулі якусь силу (простіше кажучи, штовхнути його), то кулька почне розгойдуватися на нитки, слідуючи певній траєкторії. З часом можна помітити, що траєкторія, по якій проходить куля, скорочується. У той же час кулька починає все швидше снувати туди-сюди. Це говорить про те, що частота коливань збільшується. А ось час, за який кулька повертається в початкове положення, зменшується. Адже час одного повного коливання, як ми з'ясували раніше, і називається періодом. Якщо одна величина зменшується, а інша збільшується, то кажуть про зворотної пропорційності. Ось ми і дісталися до першого моменту, на підставі якого будуються формули для визначення періоду коливань. Якщо ж ми візьмемо для проведення пружинний маятник, то там закон буде спостерігатися трохи в іншому вигляді. Для того щоб він був найбільш наочно представлений, наведемо систему в рух у вертикальній площині. Щоб було зрозуміліше, спочатку варто було сказати, що собою являє пружинний маятник. З назви зрозуміло, що в його конструкції повинна бути пружина. І це дійсно так. Знову ж таки, у нас є горизонтальна площина на опорах, до якої підвішується пружина певної довжини і жорсткості. До неї, в свою чергу, підвішується грузик. Це може бути циліндр, куб чи інша постать. Це може бути навіть якийсь сторонній предмет. У будь-якому випадку, при виведенні системи з положення рівноваги, вона почне здійснювати затухаючі коливання. Найбільш чітко проглядається збільшення частоти саме у вертикальній площині, без жодного відхилення. На цьому з дослідами можна закінчити.
Отже, якщо вивести таку систему з рівноваги, прикласти до кулі якусь силу (простіше кажучи, штовхнути його), то кулька почне розгойдуватися на нитки, слідуючи певній траєкторії. З часом можна помітити, що траєкторія, по якій проходить куля, скорочується. У той же час кулька починає все швидше снувати туди-сюди. Це говорить про те, що частота коливань збільшується. А ось час, за який кулька повертається в початкове положення, зменшується. Адже час одного повного коливання, як ми з'ясували раніше, і називається періодом. Якщо одна величина зменшується, а інша збільшується, то кажуть про зворотної пропорційності. Ось ми і дісталися до першого моменту, на підставі якого будуються формули для визначення періоду коливань. Якщо ж ми візьмемо для проведення пружинний маятник, то там закон буде спостерігатися трохи в іншому вигляді. Для того щоб він був найбільш наочно представлений, наведемо систему в рух у вертикальній площині. Щоб було зрозуміліше, спочатку варто було сказати, що собою являє пружинний маятник. З назви зрозуміло, що в його конструкції повинна бути пружина. І це дійсно так. Знову ж таки, у нас є горизонтальна площина на опорах, до якої підвішується пружина певної довжини і жорсткості. До неї, в свою чергу, підвішується грузик. Це може бути циліндр, куб чи інша постать. Це може бути навіть якийсь сторонній предмет. У будь-якому випадку, при виведенні системи з положення рівноваги, вона почне здійснювати затухаючі коливання. Найбільш чітко проглядається збільшення частоти саме у вертикальній площині, без жодного відхилення. На цьому з дослідами можна закінчити. 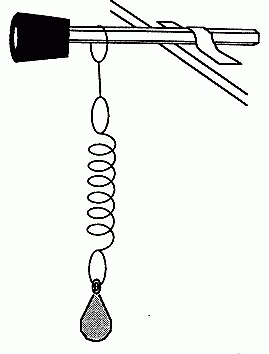 Отже, в їх ході ми з'ясували, що період і частота коливань це дві фізичні величини, які мають зворотну залежність.
Отже, в їх ході ми з'ясували, що період і частота коливань це дві фізичні величини, які мають зворотну залежність. 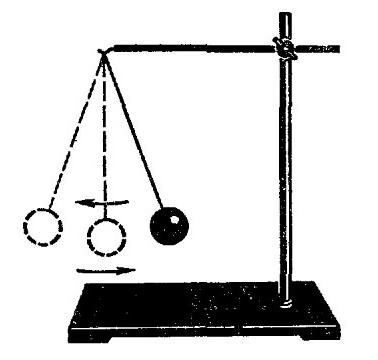 Під формулою періоду вільних коливань розуміють ті формули, які ми розібрали в двох раніше наведених задачах. Складають також рівняння вільних коливань, але там мова йде вже про зсувах і координати, а це питання належить вже до іншої статті.
Під формулою періоду вільних коливань розуміють ті формули, які ми розібрали в двох раніше наведених задачах. Складають також рівняння вільних коливань, але там мова йде вже про зсувах і координати, а це питання належить вже до іншої статті.
Визначення та фізичний зміст
Періодом коливань називається такий проміжок часу, при якому тіло або система здійснюють одне коливання (обов'язково повне). Паралельно можна відзначити параметр, при виконанні якого коливання може вважатися повним. В ролі такої умови виступає повернення тіла в його первісний стан (до первісної координаті). Дуже добре проводиться аналогія з періодом функції. Помилково, до речі, думати, що вона має місце виключно у звичайній і вищої математики. Як відомо, ці дві науки нерозривно пов'язані. І з періодом функцій можна зіткнутися не тільки при рішенні тригонометричних рівнянь, але і в різних розділах фізики, а саме мова йде про механіці, оптиці та інших. При перенесенні періоду коливань з математики у фізику під ним потрібно розуміти просто фізичну величину (а не функцію), яка має пряму залежність від минаючого часу.Які бувають коливання?
Коливання поділяються на гармонійні та ангармоничні, а також на періодичні і неперіодичні. Логічно було б припустити, що у випадку гармонічних коливань вони здійснюються згідно з деякою гармонічної функції. Це може бути як синус, так і косинус. При цьому в справі можуть виявитися і коефіцієнти стиснення-розтягування і збільшення-зменшення. Також коливання бувають затухаючими. Тобто, коли на систему діє певна сила, яка поступово "гальмує" самі коливання. При цьому період стає менше, в той час як частота коливань незмінно збільшується. Дуже добре демонструє таку от фізичну аксіому найпростіший досвід з використанням маятника. Він може бути пружинного виду, а також математичного. Це неважливо. До речі, період коливань у таких системах буде визначатися різними формулами. Але про це трішки пізніше. Зараз же наведемо приклади.Досвід з маятниками
Взяти першим можна будь маятник, різниці ніякої не буде. Закони фізики на то і закони фізики, що вони дотримуються в будь-якому випадку. Але чомусь більше до душі математичний маятник. Якщо хтось не знає, що він собою представляє: це кулька на нерозтяжній нитці, який кріпиться до горизонтальної планки, прикріпленою до ніжкам (або елементів, які відіграють роль – тримати систему в рівноважному стані). Кулька краще всього брати з металу, щоб досвід був наочніше.

Позначення величин і розмірності
Зазвичай період коливань позначається латинською буквою T. Набагато рідше він може позначатися по-іншому. Частота ж позначається буквою µ ("Мю"). Як ми говорили на самому початку, період це не що інше, як час, за який в системі відбувається повне коливання. Тоді розмірністю періоду буде секунда. А так як період і частота назад пропорційні, то розмірністю частоти буде одиниця, поділена на секунду. У записі завдань все буде виглядати таким чином: T (с), µ (1/с).Формула для математичного маятника. Завдання №1
Як і у випадку з дослідами, я вирішив насамперед розібратися з математичним маятником. Детально вдаватися до виведення формули ми не будемо, оскільки така задача поставлена спочатку не була. Та й висновок сам по собі громіздкий. Але ось з самими формулами ознайомимося, з'ясуємо, що за величини в них входять. Отже, формула періоду коливань математичного маятника має наступний вигляд: Де l – довжина нитки, п = 314 а g – прискорення вільного падіння (98 м/с^2). Ніяких труднощів формула викликати не повинна. Тому без додаткових питань перейдемо відразу до розв'язання задачі на визначення періоду коливання математичного маятника. Металева куля масою 10 грам підвішений на нерозтяжній нитці довжиною 20 сантиметрів. Розрахуйте період коливання системи, прийнявши її за математичний маятник. Рішення дуже просте. Як і у всіх задачах з фізики, необхідно максимально спростити її за рахунок відкидання непотрібних слів. Вони включаються в контекст для того щоб заплутати вирішального, але насправді ніякого ваги абсолютно не мають. У більшості випадків, зрозуміло. Тут можна виключити момент з "нерозтяжній ниткою". Це словосполучення не повинно вводити в ступор. А так як маятник у нас математичний, маса вантажу нас не повинна цікавити. Тобто слова про 10 грамах теж просто покликані заплутати учня. Але ми знаємо, що формулою маса відсутня, тому зі спокійною совістю можемо приступати до виконання. Отже, беремо формулу і просто підставляємо в неї величини, оскільки необхідно визначити період системи. Оскільки додаткових умов не було вказано, округлювати значення будемо до 3-го знака після коми, як і прийнято. Перемноживши і поділивши величини, отримаємо, що період коливань дорівнює 0886 секунд. Задача вирішена.Формула для пружинного маятника. Завдання №2
Формули маятників мають загальну частину, а саме 2п. Ця величина є одразу у двох формулах, але різняться вони подкоренним виразом. Якщо в задачі, що стосується періоду пружинного маятника, вказана маса вантажу, то уникнути обчислень з її застосування неможливо, як це було у випадку з математичним маятником. Але лякатися не варто. Ось так виглядає формула періоду для пружинного маятника: В ній m – маса підвішеного до пружини вантажу, k – коефіцієнт жорсткості пружини. В завданні значення коефіцієнта може бути приведене. Але якщо у формулі математичного маятника особливо не розгуляєшся – все-таки 2 величини з 4 є константами – то тут додається 3 параметр, який може змінюватися. І на виході ми маємо 3 змінних: період (частота) коливань, коефіцієнт жорсткості пружини, маса підвішеного вантажу. Завдання може бути зорієнтована на знаходження будь-якого з цих параметрів. Знову шукати період було б занадто легко, тому ми трохи змінимо умову. Знайдіть коефіцієнт жорсткості пружини, якщо час повного коливання становить 4 секунди, а маса вантажу пружинного маятника дорівнює 200 грамам. Для вирішення будь-якої фізичної задачі добре б спочатку зробити малюнок і написати формули. Вони тут – половина справи. Записавши формулу, необхідно виразити коефіцієнт жорсткості. Він у нас перебуває під коренем, тому обидві частини рівняння зведемо в квадрат. Щоб позбутися від дробу, помножимо частини на k. Тепер залишимо в лівій частині рівняння тільки коефіцієнт, тобто розділимо частини на T^2. В принципі, задачку можна було б ще трохи ускладнити, задавши не період в числах, а частоту. У будь-якому випадку, при підрахунках і заокругленнях (ми домовилися округляти до 3-го знака після коми), вийде, що k = 0157 Н/м.Період вільних коливань. Формула періоду вільних коливань

Поради для вирішення завдань, пов'язаних з періодом
1) Перш ніж братися за завдання, запишіть формулу, яка з нею пов'язана. 2) Найпростіші завдання не вимагають малюнків, але у виняткових випадках їх потрібно буде зробити. 3) Намагайтеся позбавлятися від коренів і знаменників, якщо це можливо. Записаний у рядок рівняння, що не має знаменника, вирішувати набагато зручніше і простіше.Схожі добрі поради по темі

Динаміка долара: причини коливань
Долар – це національна валюта США і одна з найстабільніших у світі. Її вплив дуже велике. Американська валюта є певним еталоном, щодо якого

Що таке період? Значення багатогранного поняття
На світі є багато конкретних і абстрактних понять, досить звичних і багатозначних, вживаються в багатьох галузях науки і повсякденному житті. Серед
Рівноприскорений рух. Завдання і формули
Найважливішою характеристикою при русі тіла є його швидкість. Знаючи її, а також деякі інші параметри, ми завжди можемо визначити час руху, пройдену
Доцентрове прискорення виведення формули і практичне застосування
Доцентровеприскорення супроводжує нас всюди. Саме воно змушує нашу Землю обертатися навколо Сонця. Виникаюча при цьому сила тяжіння дозволяє нам
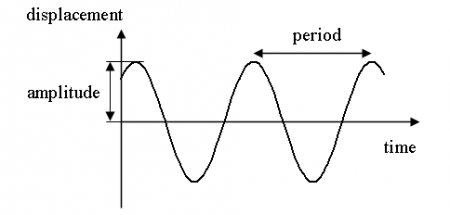
Вільні коливання. Загальні відомості
У цій статті ми поговоримо про вільні коливання. Розглянемо їх приклади: математичний і пружинний маятники, а також коливальний контур.
Обертальний рух тіла. Закон обертального руху
У цій статті описується важливий розділ механіки - "Кінематика та динаміка обертального руху". Дані основні поняття і формули.