Метод Гаусса для вирішення матриць. Рішення системи лінійних рівнянь методом Гауса
Ще з початку XVI-XVIII століть математики посилено почали вивчати функції, завдяки яким так багато в нашому житті змінилося. Комп'ютерна техніка без цих знань просто не існувала б. Для вирішення складних завдань, лінійних рівнянь і функцій були створені різні концепції, теореми та методики рішення. Одним із таких універсальних і раціональних способів і методик розв'язання лінійних рівнянь і їх систем став і метод Гаусса. Матриці, їх ранг, детермінант - все можна порахувати, не використовуючи складних операцій.
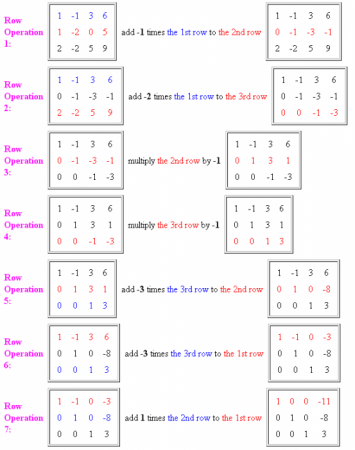
Можливо, деякі позначення не зовсім зрозумілі, тому необхідно розглянути всі на прикладі. Припустимо, є система: x+y=1; 2x-3y=6. Вона складається всього з двох рівнянь, в яких 2 невідомі. Система буде мати рішення тільки в тому випадку, якщо ранг її матриці буде дорівнювати рангу розширеної матриці. Що таке ранг? Це число незалежних рядків системи. У нашому випадку ранг матриці 2. Матриця А буде складатися з коефіцієнтів, що знаходяться біля невідомих, а розширену матрицю вписуються і коефіцієнти, що знаходяться за знаком «=». Переписуючи систему в матричний вигляд і здійснюючи її рішення, можна множити всі елементи ряду на один і той же коефіцієнт. Для того щоб перетворити матрицю в канонічний вигляд, можна міняти місцями два паралельних ряди. Канонічний вид передбачає, що всі елементи матриці, що розміщені на головній діагоналі, стають одиницями, а решта - нулями. Відповідні елементи паралельних рядів матриці можна додавати один до іншого.
Перепишемо її у розширену матрицю. 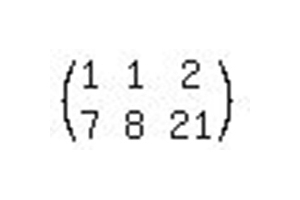 Щоб вирішити дану систему лінійних рівнянь, потрібно зробити лише дві операції. Нам необхідно привести матрицю до канонічного виду, щоб по головній діагоналі стояли одиниці. Так, перекладаючи з матричного виду назад у систему, ми отримаємо рівняння: 1x+0y=b1 і 0x+1y=b2 де b1 і b2 - отримані відповіді в процесі вирішення.
Щоб вирішити дану систему лінійних рівнянь, потрібно зробити лише дві операції. Нам необхідно привести матрицю до канонічного виду, щоб по головній діагоналі стояли одиниці. Так, перекладаючи з матричного виду назад у систему, ми отримаємо рівняння: 1x+0y=b1 і 0x+1y=b2 де b1 і b2 - отримані відповіді в процесі вирішення. Перша дія при вирішенні розширеної матриці буде таким: перший ряд необхідно помножити на -7 і додати відповідно відповідальні елементи до другої рядку, щоб позбутися одного невідомого у другому рівнянні. Так як рішення рівнянь методом Гауса передбачає привида матриці до канонічного виду, тоді необхідно і з першим рівнянням виконати ті ж операції і прибрати другу змінну. Для цього другу рядка віднімаємо від першою і отримуємо необхідну відповідь - рішення СЛАУ. Або, як показано на малюнку, другий рядок множимо на коефіцієнт -1 і додаємо до першої рядку елементи другого ряду. Це одне і те ж. Як бачимо, наша система вирішена методом Жордана-Гауса. Переписуємо її в необхідну форму: x=-5 y=7. 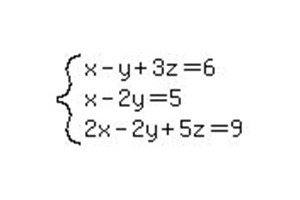 Як і в попередньому прикладі, переписуємо систему вигляд розширеної матриці і починаємо приводити її до канонічного виду.
Як і в попередньому прикладі, переписуємо систему вигляд розширеної матриці і починаємо приводити її до канонічного виду. 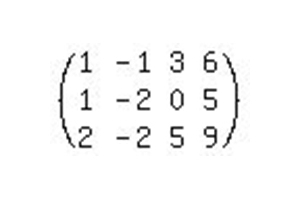 Для рішення цієї системи знадобиться зробити набагато більше дій, ніж в попередньому прикладі.
Для рішення цієї системи знадобиться зробити набагато більше дій, ніж в попередньому прикладі. Спочатку необхідно зробити в першому стовпці один одиничний елемент і інші нулі. Для цього помножимо перше рівняння на -1 і додаємо до нього друге рівняння. Важливо запам'ятати, що перший рядок ми переписуємо у первісному вигляді, а другу - вже в зміненому. Далі прибираємо цю ж першу невідому з третього рівняння. Для цього елементи першого рядка множимо на -2 і додаємо їх до третього ряду. Тепер перша і друга рядка переписуються в первісному вигляді, а третя - із змінами. Як видно з результату, ми отримали першу одиницю на початку головної діагоналі матриці та інші нулі. Ще кілька кроків, і система рівнянь методом Гауса буде достовірно вирішена. Тепер необхідно виконати операції над іншими елементами рядів. Третє і четверте дію можна об'єднати в одне. Потрібно розділити другу і третю рядок на -1 щоб позбутися від мінусових одиниць по діагоналі. Третій рядок ми вже привели до необхідного виду. Далі приведемо до канонічного виду другий рядок. Для цього елементи третього ряду множимо на -3 і додаємо їх до другого рядка матриці. З результату видно, що друга рядок теж приведена до необхідної нам формі. Залишилося виконати ще кілька операцій і прибрати коефіцієнти невідомих з першого рядка. Щоб з другого елементу рядка зробити 0 необхідно помножити третій рядок на -3 і додати її до першого ряду. Наступним вирішальним етапом буде додатком до першої рядку необхідні елементи другого ряду. Так ми отримуємо канонічний вигляд матриці, а, відповідно, і відповідь. Як видно, рішення рівнянь методом Гауса досить просте.
Що являє собою СЛАР
У математиці існує поняття СЛАУ - система лінійних алгебраїчних рівнянь. Що ж вона собою являє? Це набір з m рівнянь з заданими n невідомими величинами, зазвичай обозначающимися як x, y, z, або x 1 , x 2 x n, або іншими символами. Вирішити методом Гаусса дану систему - означає знайти всі шукані невідомі. Якщо система має однакове число невідомих і рівнянь, тоді вона називається системою n-го порядку.Найбільш популярні методи розв'язання СЛАР
В навчальних закладах середньої освіти вивчають різні методики вирішення таких систем. Найчастіше це прості рівняння, що складаються з двох невідомих, тому будь-який існуючий метод для пошуку відповіді на них не займе багато часу. Це може бути як метод підстановки, коли з одного рівняння виводиться інше і підставляється в початкове. Або метод почленного віднімання і додавання. Але найбільш легким і універсальним вважається метод Гаусса. Він дає можливість вирішувати рівняння з будь-якою кількістю невідомих. Чому саме ця методика вважається раціональною? Все просто. Матричний спосіб хороший тим, що тут не потрібно по кілька разів переписувати непотрібні символи у вигляді невідомих, достатньо виконати арифметичні операції над коефіцієнтами - і вийде достовірний результат.Де використовуються СЛАУ на практиці
Рішенням СЛАР є точки перетину прямих на графіках функцій. У наш високотехнологічний комп'ютерний вік людям, які тісно пов'язані з розробкою ігор і інших програм, необхідно знати, як вирішувати такі системи, що вони представляють і як перевірити правильність отриманого результату. Найбільш часто програмісти розробляють спеціальні програми-обчислювачі лінійної алгебри, сюди входить і система лінійних рівнянь. Метод Гауса дозволяє вирахувати всі існуючі рішення. Також використовуються і інші спрощені формули й методики.Критерій сумісності СЛАР
Таку систему можна вирішити тільки в тому випадку, якщо вона сумісна. Для зрозумілості уявімо СЛАР у вигляді Ax=b. Вона має рішення, якщо rang(A) дорівнює rang(A,b). У цьому випадку (A,b) – це матриця розширеного види, яку можна одержати з матриці А, переписавши її з вільними членами. Виходить, що вирішити лінійні рівняння методом Гауса досить легко.Можливо, деякі позначення не зовсім зрозумілі, тому необхідно розглянути всі на прикладі. Припустимо, є система: x+y=1; 2x-3y=6. Вона складається всього з двох рівнянь, в яких 2 невідомі. Система буде мати рішення тільки в тому випадку, якщо ранг її матриці буде дорівнювати рангу розширеної матриці. Що таке ранг? Це число незалежних рядків системи. У нашому випадку ранг матриці 2. Матриця А буде складатися з коефіцієнтів, що знаходяться біля невідомих, а розширену матрицю вписуються і коефіцієнти, що знаходяться за знаком «=».
Чому СЛАУ можна подати в матричному вигляді
Виходячи з критерію сумісності за доведеною теоремою Кронекера-Капеллі, систему лінійних алгебраїчних рівнянь можна представити у матричному вигляді. Застосовуючи каскадний метод Гаусса, можна вирішити матрицю і отримати єдиний достовірний відповідь на всю систему. Якщо ранг звичайної матриці дорівнює рангу її розширеної матриці, але при цьому менше кількості невідомих, тоді система має нескінченну кількість відповідей.Перетворення матриць
Перш ніж переходити до вирішення матриць, необхідно знати, які дії можна виконувати над їх елементами. Існує кілька елементарних перетворень:Метод Жордана-Гауса
Суть розв'язання систем лінійних однорідних і неоднорідних рівнянь методом Гауса в тому, щоб поступово виключити невідомі. Припустимо, у нас є система з двох рівняння, в яких дві невідомі. Щоб їх знайти, необхідно перевірити систему на сумісність. Рівняння методом Гауса вирішується дуже просто. Необхідно виписати коефіцієнти, що знаходяться біля кожного невідомого в матричний вигляд. Для рішення системи знадобиться виписати розширену матрицю. Якщо одне з рівнянь містить меншу кількість невідомих, тоді на місце пропущеного елемента необхідно поставити «0». До матриці застосовуються всі відомі методи перетворення: множення, ділення на число, додавання відповідних елементів рядів один до одного і інші. Виходить, що в кожному ряду необхідно залишити одну змінну зі значенням «1», інші призвести до нульового увазі. Для більш точного розуміння необхідно розглянути метод Гаусса на прикладах.Простий приклад рішення системи 2х2
Для початку візьмемо просту систему алгебраїчних рівнянь, в якій буде 2 невідомих.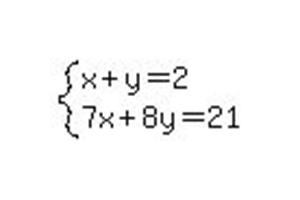
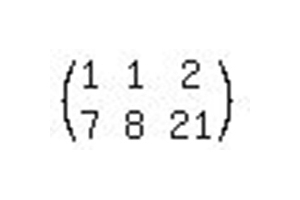
Приклад розв'язання СЛАР 3х3
Припустимо, що у нас є більш складна система лінійних рівнянь. Метод Гаусса дає можливість вирахувати відповідь навіть для самої, здавалося б, заплутаної системи. Тому, щоб більш глибоко вникнути в методику розрахунку, можна переходити до більш складного прикладу з трьома невідомими.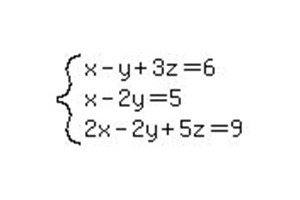
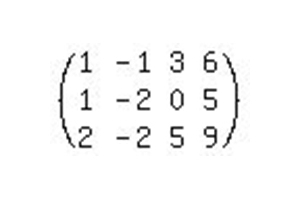
Приклад рішення системи рівнянь 4х4
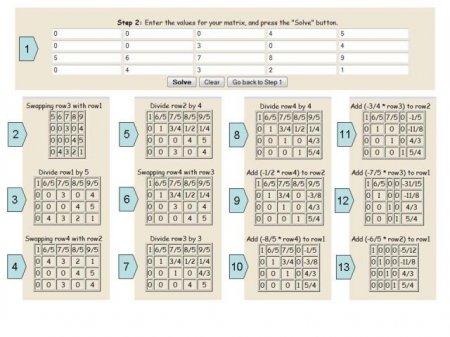
Деякі більш складні системи рівнянь можна вирішити методом Гауса за допомогою комп'ютерних програм. Необхідно вбити в існуючі порожні клітинки коефіцієнти при невідомих, і програма сама покроково розрахує необхідний результат, докладно описуючи кожну дію. Нижче описана покрокова інструкція рішення такого прикладу. • У першій дії у порожні клітинки вписуються вільні коефіцієнти і числа при невідомих. Таким чином, виходить така ж розширена матриця, яку ми пишемо вручну. • Далі міняються місцями всі рядки, щоб можна було виразити по головній діагоналі поодинокі елементи. • І проводяться всі необхідні арифметичні операції, щоб привести розширену матрицю до канонічного виду. Необхідно розуміти, що не завжди відповідь на систему рівнянь - це цілі числа. Іноді рішення може бути з дробових чисел.Перевірка правильності рішення
Метод Жордана-Гауса передбачає перевірку правильності результату. Для того щоб дізнатися, чи правильно пораховані коефіцієнти, необхідно всього-навсього підставити результат у початкову систему рівнянь. Ліва сторона рівняння має відповідати правій стороні, що знаходиться за знаком "дорівнює". Якщо відповіді не збігаються, тоді необхідно перераховувати заново систему або спробувати застосувати до неї інший відомий вам метод розв'язання СЛАР, такий як підстановка або почленное віднімання і додавання. Адже математика – це наука, яка має величезну кількість різних методик рішення. Але пам'ятайте: результат повинен бути завжди один і той же, незалежно від того, який метод рішення ви використовували.Метод Гауса: найбільш часто зустрічаються помилки при розв'язанні СЛАР
Під час розв'язання лінійних систем рівнянь найчастіше виникають такі помилки, як неправильний перенесення коефіцієнтів матричний вигляд. Бувають системи, в яких відсутні в одному з рівнянь деякі невідомі, тоді, переносячи дані в розширену матрицю, їх можна втратити. В результаті при вирішенні даної системи результат може не відповідати дійсному. Ще однією з головних помилок може бути неправильне виписування кінцевого результату. Потрібно чітко розуміти, що перший коефіцієнт буде відповідати першому невідомому з системи, другий - другого, і так далі. Метод Гаусса докладно описує рішення лінійних рівнянь. Завдяки йому легко зробити необхідні операції і знайти вірний результат. Крім того, це універсальний засіб для пошуку достовірної відповіді на рівняння будь-якої складності. Може бути, тому так часто використовують при розв'язанні СЛАР.Схожі добрі поради по темі

Закон Клапейрона-Менделєєва: формула, формулювання, використання
Кожен школяр, який навчається у десятому класі на одному з уроків фізики стикається з законом Клапейрона-Менделєєва, вивчає формули, формулювання,

Гвинтівка Гауса – технологія та принципи функціонування
Кожному любителю наукової фантастики добре знайоме електромагнітна зброя. Зображуються подібні технології у вигляді поєднання механічних, електронних
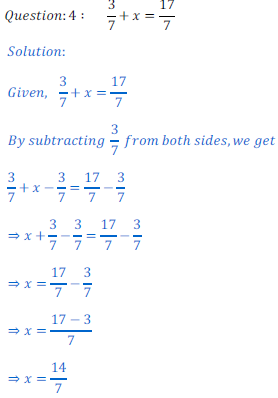
Знайти корінь рівняння? Це просто!
В математиці зустрічаються різноманітні рівняння. Їх завжди потрібно вирішувати, тобто шукати всі числа, які зроблять його вірним. Шляхи пошуку

Територія Росії, її особливості і рельєф
Дана стаття спрямована на те, щоб розкрити кілька цікавих і в той же час досить важливих питань. Читач не тільки дізнається про те, скільки територія
Деякі моменти про те, як виконується рішення нерівностей
Одна з тем, яка вимагає від учнів максимуму уваги і посидючості, це рішення нерівностей. Такі схожі на рівняння і при цьому сильно від них
Гармата Гауса - зброя майбутнього?
Багато любителів комп'ютерних «стрілялок» неодноразово стикалися з такою зброєю, як «гармата Гауса». Що ж це за пристрій, чому воно так примітно й