Об'єм конуса, його розрахунок
Геометрія як наука сформувалася в Стародавньому Єгипті і досягла високого рівня розвитку. Відомий філософ Платон заснував Академію, де пильна увага приділялась систематизації наявних знань. Конус як одна з геометричних фігур вперше згадується у відомому трактаті Евкліда "Начала". Евклід був знайомий з працями Платона. Зараз мало хто знає, що слово "конус" в перекладі з грецької мови означає "соснова шишка". Грецький математик Евклід, який жив в Александрії, праву вважається основоположником геометричної алгебри. Стародавні греки не тільки стали наступниками знань єгиптян, але і значно розширили теорію.
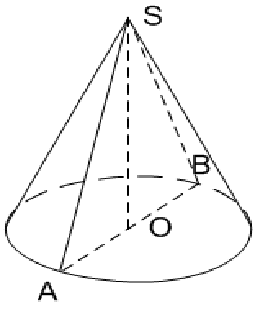 Гіпотенуза AS прямокутного трикутника AOS при обертанні навколо катета OS утворює бічну поверхню конуса, тому називається твірною. Катет OS трикутника перетворюється одночасно у висоту конуса і його вісь. Точка S стає вершиною конуса. Катет AO, описавши коло (підстава), перетворився в радіус конуса. Якщо зверху провести площину через вершину і вісь конуса, то можна побачити, що отримане осьовий переріз являє собою рівнобедрений трикутник, в якому вісь є висотою трикутника. Також часто потрібно розрахувати площу бічної поверхні тіла обертання. Площа бічної поверхні конуса дорівнює добутку половини довжини окружності підстави і твірною конуса. S=C*L/2=n*R*L/2 де C — довжина окружності основи, l — довжина твірної конуса, R — радіус підстави.
Гіпотенуза AS прямокутного трикутника AOS при обертанні навколо катета OS утворює бічну поверхню конуса, тому називається твірною. Катет OS трикутника перетворюється одночасно у висоту конуса і його вісь. Точка S стає вершиною конуса. Катет AO, описавши коло (підстава), перетворився в радіус конуса. Якщо зверху провести площину через вершину і вісь конуса, то можна побачити, що отримане осьовий переріз являє собою рівнобедрений трикутник, в якому вісь є висотою трикутника. Також часто потрібно розрахувати площу бічної поверхні тіла обертання. Площа бічної поверхні конуса дорівнює добутку половини довжини окружності підстави і твірною конуса. S=C*L/2=n*R*L/2 де C — довжина окружності основи, l — довжина твірної конуса, R — радіус підстави.
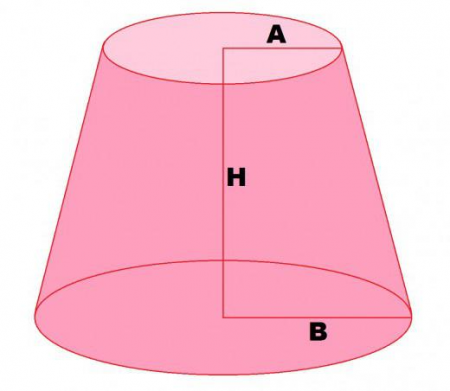
R 1 =A; R 2 =B; H=H. Якщо прямий конус утворюється обертанням прямокутного трикутника, то усічений конус — обертанням прямокутної трапеції навколо прямий боку. Обсяг усіченого конуса розраховується за наступною формулою: V=n*(R 1 2 +R 2 2 +R 1 *R 2 )*H/3.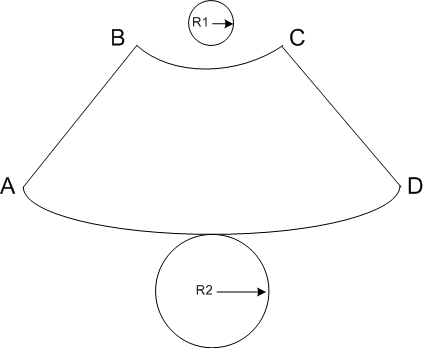 L - твірна конуса. Щоб дізнатися площа поверхні відра, яка обчислюється за наступною формулою: S=n*(R 1 +R 2 )*L, необхідно обчислити утворить. Її знаходимо з величини об'єму V=n*(R 1 2 +R 2 2 +R 1 *R 2 )*H/3. Звідси H=3V/n*(R 1 2 +R 2 2 +R 1 *R 2 ). Усічений конус утворюється обертанням прямокутної трапеції, в якій бічна сторона є твірною конуса. L 2 =(R 2 - R 1 ) 2 +H 2 . Тепер у нас є всі дані, щоб побудувати креслення відра.
L - твірна конуса. Щоб дізнатися площа поверхні відра, яка обчислюється за наступною формулою: S=n*(R 1 +R 2 )*L, необхідно обчислити утворить. Її знаходимо з величини об'єму V=n*(R 1 2 +R 2 2 +R 1 *R 2 )*H/3. Звідси H=3V/n*(R 1 2 +R 2 2 +R 1 *R 2 ). Усічений конус утворюється обертанням прямокутної трапеції, в якій бічна сторона є твірною конуса. L 2 =(R 2 - R 1 ) 2 +H 2 . Тепер у нас є всі дані, щоб побудувати креслення відра.  Обсяг конуса має купа піску чи землі, висипана на землю. При необхідності, провівши нескладні вимірювання, можна розрахувати її обсяг. У деяких викличе утруднення питання про те, як дізнатися радіус і висоту купи піску. Озброївшись рулеткою, вимірюємо коло горбка C. За формулою R=C/2n дізнаємося радіус. Перекинувши мотузку (рулетку) через вершину, знаходимо довжину твірної. А обчислити висоту за теоремою Піфагора і обсяг буде неважко. Звичайно, такий розрахунок приблизний, але дозволяє визначити, чи не обдурили вас, привізши тонну піску замість куба. Деякі будівлі мають форму усіченого конуса. Наприклад, Останкінська телевежа наближається до форми конуса. Її можна представити що складається з двох конусів, поставлених один на одного. Куполи старовинних замків і соборів являють собою конус, обсяг якого стародавні зодчі розраховували з дивовижною точністю.
Обсяг конуса має купа піску чи землі, висипана на землю. При необхідності, провівши нескладні вимірювання, можна розрахувати її обсяг. У деяких викличе утруднення питання про те, як дізнатися радіус і висоту купи піску. Озброївшись рулеткою, вимірюємо коло горбка C. За формулою R=C/2n дізнаємося радіус. Перекинувши мотузку (рулетку) через вершину, знаходимо довжину твірної. А обчислити висоту за теоремою Піфагора і обсяг буде неважко. Звичайно, такий розрахунок приблизний, але дозволяє визначити, чи не обдурили вас, привізши тонну піску замість куба. Деякі будівлі мають форму усіченого конуса. Наприклад, Останкінська телевежа наближається до форми конуса. Її можна представити що складається з двох конусів, поставлених один на одного. Куполи старовинних замків і соборів являють собою конус, обсяг якого стародавні зодчі розраховували з дивовижною точністю.  Якщо уважно придивитися до оточуючих предметів, то багато з них є конусами:
Якщо уважно придивитися до оточуючих предметів, то багато з них є конусами: воронки-лійки для наливання рідини; рупор-гучномовець; паркувальні конуси; абажур для торшера; звична новорічна ялинка; духові музичні інструменти.  Як видно з наведених прикладів, вміння розрахувати обсяг конуса, площа його поверхні необхідно в професійному та повсякденному житті. Сподіваємося, що стаття прийде вам на допомогу.
Як видно з наведених прикладів, вміння розрахувати обсяг конуса, площа його поверхні необхідно в професійному та повсякденному житті. Сподіваємося, що стаття прийде вам на допомогу.
Історія визначення конуса
Геометрія як наука з'явилася з практичних вимог будівництва та спостережень за природою. Поступово досвідчені знання узагальнювалися, а властивості одних тіл доказивались через інші. Стародавні греки ввели поняття аксіом і доказів. Аксіомою називається твердження, отримане практичним шляхом і не потребує доказів. У своїй книзі Евкліда навів визначення конуса як фігури, яка виходить обертанням прямокутного трикутника навколо одного з катетів. Також йому належить основна теорема, яка визначає обсяг конуса. А довів цю теорему давньогрецький математик Евдокс Кнідський. Інший математик стародавньої Греції, Аполлоній Пергский, який був учнем Евкліда, розвинув і виклав теорію конічних поверхонь у своїх книгах. Йому належить визначення конічної поверхні і січної до неї. Школярі наших днів вивчають Евклидову геометрію, що зберегла основні теореми і визначення з давніх часів.Основні визначення
Прямий круговий конус утворений обертанням прямокутного трикутника навколо одного катета. Як видно, поняття конуса не змінилося з часів Евкліда.
Формула розрахунку об'єму конуса
Для розрахунку об'єму конуса використовується наступна формула: V=S*H/3 де S є площею основи конуса. Так як підстава — коло, його площа розраховується так: S=nR 2 . Звідси випливає: V=n*R 2 *H/3 де V — об'єм конуса; n — число, що дорівнює 314; R — радіус основи, що відповідає відрізку AO на малюнку 1; H — висота, рівна відрізку OS.Усічений конус, обсяг
Є прямий круговий конус. Якщо площиною, перпендикулярною висоті, відрізати верхню частину, то вийде усічений конус. Два його основи мають форму кола з радіусами R 1 і R 2 .R 1 =A; R 2 =B; H=H. Якщо прямий конус утворюється обертанням прямокутного трикутника, то усічений конус — обертанням прямокутної трапеції навколо прямий боку. Обсяг усіченого конуса розраховується за наступною формулою: V=n*(R 1 2 +R 2 2 +R 1 *R 2 )*H/3.
Конус і його перетин площиною
Перу давньогрецького математика Аполлонія Пергского належить теоретичний працю «Конічні перетини». Завдяки його роботам у геометрії з'явилися визначення кривих: параболи, еліпси, гіперболи. Розглянемо, причому тут конус. Візьмемо прямий круговий конус. Якщо площина перетинає його перпендикулярно осі, то в розрізі утворюється коло. Коли січна перетинає конус під кутом до осі, то в розрізі виходить еліпс. Січна площина, перпендикулярна основи і паралельна осі конуса, утворює на поверхні гіперболу. Площина, разрезающая конус під кутом до основи і паралельна дотичній до конусу, створює на поверхні криву, яку назвали параболою.Рішення завдання
Навіть просте завдання про те, як виготовити відро певного обсягу, вимагає знань. Наприклад, необхідно розрахувати розміри відра, щоб воно мало об'єм 10 літрів. Дано: V=10 л=10 дм 3 ; R 1 =15 см; R 2 =25 см. Розгортка конуса має вигляд, схематично наведений на малюнку 3.
Чому пожежні відра мають форму конуса?
Хто замислювався, чому пожежні відра мають, здавалося б, дивну конічну форму? А це не просто так. Виявляється, конічне відро при гасінні пожежі має багато переваг перед звичайним, що мають форму усіченого конуса. По-перше, як виявляється, пожежне відро швидше наповнюється водою і при перенесенні вона не розхлюпується. Конус, обсяг якого більше звичайного відра, за один раз дозволяє перенести більше води. По-друге, воду з нього можна виплеснути на більшу відстань, ніж з звичайного відра. По-третє, якщо конічне відро зірветься з рук і впаде у вогонь, то вся вода виливається на вогнище загоряння. Всі перераховані фактори дозволяють заощадити час — головний фактор при гасінні пожежі.Практичне застосування
У школярів часто виникає питання про те, навіщо вчити, як розраховувати обсяг різних геометричних тіл, в тому числі конуса. А інженери-конструктори постійно стикаються з необхідністю розрахувати обсяг конічних частин деталей механізмів. Це наконечники свердел, частини токарних і фрезерних верстатів. Форма конуса дозволять свердел легко входити в матеріал, не вимагаючи первісної намітки спеціальним інструментом.


Схожі добрі поради по темі

Зображення геометричних фігур для дітей
Займатися освітою своїх дітей з самого раннього віку - одна з найважливіших завдань батьків. Потрібно вчити дітей рахувати, читати невеликі

"Життя після життя": відгуки про фільм, актори і ролі
Кінофільм "Життя після життя" розповідає про долю дівчини на ім'я Марія, яка, вийшовши заміж не по любові, виявляє, що її чоловік приховує від усіх

Педологія – це Розбираємося в понятті
Педологія – це наука, що поєднала в собі підходи медицини, біології, педагогіки і психотехніки до розвитку дитини. І хоча термін вона застаріла і

Чому наука про рослини називається ботанікою? Ботаніка - наука про рослини
Ботаніка, як і назви багатьох інших наук, має грецькі корені. "Ботаніка" - похідне від слова "ботанэ", воно означало все, що відносилося до рослин.

Давньогрецький математик Евклід: біографія вченого, відкриття та цікаві факти
Пропонуємо вам познайомитися з таким великим математиком, як Евклід. Біографія, короткий зміст основної його праці та деякі цікаві факти про цього

Висловлювання про математику великих математиків. Вислови великих людей про математику
Висловлювання про математику як про абстрактну науку можна зустріти не тільки в історичних джерелах, але і в побутових умовах, де потрібно вести