Подання чисел в комп'ютері. Представлення цілих і дійсних чисел у пам'яті комп'ютера
Кожному, хто хоч раз в житті замислювався про те, щоб стати "айтішником" або системним адміністратором, та й просто зв'язати долю з обчислювальною технікою, знання про те, як відбувається представлення чисел в пам'яті комп'ютера, абсолютно необхідно. Адже саме на цьому ґрунтуються мови програмування низького рівня, такі як Assembler. Тому сьогодні ми розглянемо представлення чисел в комп'ютері і їх розміщення в комірках пам'яті.

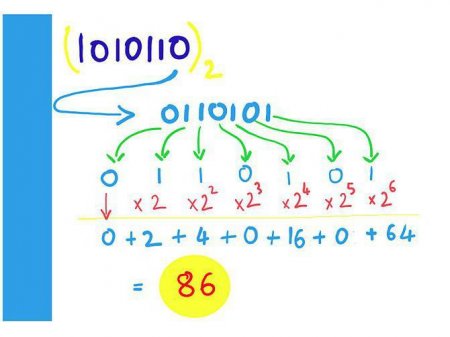
Щоб перевести звичні для нас десяткові числа до виду, зрозумілому комп'ютера, потрібно скористатися описаним нижче алгоритмом. Існують і спеціалізовані калькулятори. Отже, для того щоб перевести число в двійкову систему числення, треба взяти вибране нами значення і поділити його на 2. Після цього ми отримаємо результат і залишок (0 або 1). Результат знову ділимо 2 і запам'ятовуємо залишок. Дану процедуру потрібно повторювати до тих пір, поки в результаті також не виявиться 0 або 1. Потім записуємо кінцеве значення та залишки в зворотному порядку, як ми їх отримували. Саме так і відбувається подання чисел в комп'ютері. Будь-яке число записується в двійковій формі, а потім займає комірку пам'яті.
Для зберігання великих чисел використовуються клітинки. Кожна така одиниця містить до 8 біт інформації. Тому можна зробити висновок, що мінімальне значення в кожному відрізку пам'яті може становити 1 байт або бути восьмизначними двійковим числом.
Х = 1 x 2 7 + 1 x 2 6 + 1 x 2 5 + 1 x 2 4 + 1 x 2 3 + 1 x 2 2 + 1 x 2 1 + 1 x 2 0 = 1 x 2 8 - 1 = 255. Тепер ми бачимо, що в одній комірці пам'яті може розташовуватися значення від 0 до 255. Однак це відноситься виключно до цілим невід'ємним числом. Якщо ж комп'ютера знадобиться записати від'ємне значення, все пройде трохи по-іншому.
Якщо цифра негативна, то записується "1", якщо позитивна, то "0". Для простоти запам'ятовування можна провести таку аналогію: якщо знак є, то ставимо 1 якщо його немає, то нічого (0). Решта 15 біт інформації відводяться під число. Аналогічно попередньому випадку, в них можна помістити максимум п'ятнадцять одиниць. Варто відзначити, що запис негативних і позитивних чисел істотно відрізняється друг від друга. Для того щоб розмістити в 2 комірках пам'яті значення більше нуля або дорівнює йому, використовується так званий прямий код. Дана операція проводиться так само, як і було описано, а максимальне А = 32766 якщо використовувати десяткову систему числення. Відразу хочеться зазначити, що в даному випадку "0" ставиться до позитивних. Спочатку записується модуль від'ємного числа в двійковому численні. Тобто комп'ютер запам'ятовує аналогічне, але позитивне значення. Потім проводиться інвертування кожного біта пам'яті. Для цього всі одиниці замінюються нулями і навпаки. Додаємо "1" до отриманого результату. Це і буде додатковий код. Наведемо наочний приклад. Нехай у нас є число Х = - 131. Спочатку отримуємо його модуль |Х|= 131. Потім переводимо в двійкову систему і записуємо в 16 осередків. Отримаємо Х = 0000000010000011. Після інвертування Х=1111111101111100. Додаємо до нього "1" і отримуємо зворотний код Х=1111111101111101. Для запису до 16-бітну комірку пам'яті мінімальним числом є Х = - (2 15 ) = - 32767.
Процес запису абсолютно не відрізняється від представленого вище. Так що ми просто приведемо діапазон чисел, які можуть зберігатися в даному типі. Х мах =2147483 647. Х min = - 2147483 648. Даних значень в більшості випадків досить для того, щоб записувати та проводити операції з даними. Подання дійсних чисел у комп'ютері має свої переваги і недоліки. З одного боку, дана методика дозволяє простіше проводити операції між цілочисельними значеннями, що значно прискорює роботу процесора. З іншого боку, цього діапазону недостатньо для вирішення більшості завдань економіки, фізики, арифметики та інших наук. Тому тепер ми розглянемо чергову методику для сверхвеличин.

Система числення
Якщо ви читаєте цю статтю, то, швидше за все, уже знаєте про це, але варто повторити. Всі дані в персональному комп'ютері зберігаються в двійковій системі числення. Це означає, що будь-яке число необхідно представити у відповідній формі, тобто складається з нулів та одиниць.Щоб перевести звичні для нас десяткові числа до виду, зрозумілому комп'ютера, потрібно скористатися описаним нижче алгоритмом. Існують і спеціалізовані калькулятори. Отже, для того щоб перевести число в двійкову систему числення, треба взяти вибране нами значення і поділити його на 2. Після цього ми отримаємо результат і залишок (0 або 1). Результат знову ділимо 2 і запам'ятовуємо залишок. Дану процедуру потрібно повторювати до тих пір, поки в результаті також не виявиться 0 або 1. Потім записуємо кінцеве значення та залишки в зворотному порядку, як ми їх отримували. Саме так і відбувається подання чисел в комп'ютері. Будь-яке число записується в двійковій формі, а потім займає комірку пам'яті.
Пам'ять
Як вам повинно бути відомо, мінімальна одиниця вимірювання інформації-1 біт. Як ми вже з'ясували, подання чисел в комп'ютері відбувається в двійковому форматі. Таким чином, кожен біт пам'яті буде зайнятий одним значенням – 1 або 0.Для зберігання великих чисел використовуються клітинки. Кожна така одиниця містить до 8 біт інформації. Тому можна зробити висновок, що мінімальне значення в кожному відрізку пам'яті може становити 1 байт або бути восьмизначними двійковим числом.
Цілі
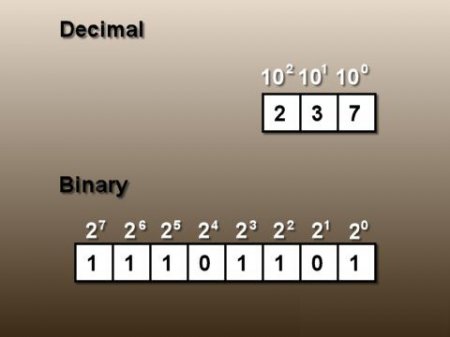
Нарешті ми підібралися до безпосереднього розміщення даних в комп'ютері. Як було вже сказано, насамперед процесор переводить інформацію у двійковий формат, а тільки потім розміщує в пам'яті. Почнемо ми з самого простого варіанту, яким є подання цілих чисел в комп'ютері. Пам'ять ПК відводить під цей процес до смішного малу кількість осередків – всього одну. Таким чином, максимум в одному слоті можуть бути значення від 0 до 11111111. Давайте переведемо максимальне число в звичну нам форму запису.Х = 1 x 2 7 + 1 x 2 6 + 1 x 2 5 + 1 x 2 4 + 1 x 2 3 + 1 x 2 2 + 1 x 2 1 + 1 x 2 0 = 1 x 2 8 - 1 = 255. Тепер ми бачимо, що в одній комірці пам'яті може розташовуватися значення від 0 до 255. Однак це відноситься виключно до цілим невід'ємним числом. Якщо ж комп'ютера знадобиться записати від'ємне значення, все пройде трохи по-іншому.
Від'ємні числа
Тепер давайте подивимося, як відбувається представлення чисел в комп'ютері, якщо вони є негативними. Для розміщення значення, яке менше нуля, відводиться дві комірки пам'яті, або 16 біт інформації. При цьому 15 йдуть під саме число, а перший (крайній лівий) біт надається під відповідний знак.Якщо цифра негативна, то записується "1", якщо позитивна, то "0". Для простоти запам'ятовування можна провести таку аналогію: якщо знак є, то ставимо 1 якщо його немає, то нічого (0). Решта 15 біт інформації відводяться під число. Аналогічно попередньому випадку, в них можна помістити максимум п'ятнадцять одиниць. Варто відзначити, що запис негативних і позитивних чисел істотно відрізняється друг від друга. Для того щоб розмістити в 2 комірках пам'яті значення більше нуля або дорівнює йому, використовується так званий прямий код. Дана операція проводиться так само, як і було описано, а максимальне А = 32766 якщо використовувати десяткову систему числення. Відразу хочеться зазначити, що в даному випадку "0" ставиться до позитивних.
Приклади
Представлення цілих чисел у пам'яті комп'ютера не є такою вже важким завданням. Хоча вона трохи ускладнюється, якщо мова йде про негативному значенні. Для запису числа, яке менше нуля, використовується додатковий код. Щоб його отримати, машина виробляє ряд допоміжних операцій.Довгі цілі
Як бачите, подання дійсних чисел у комп'ютері не так вже й складно. Однак розглянутого діапазону може не вистачати для більшості операцій. Тому, для того щоб розмістити великі числа, комп'ютер виділяє з пам'яті 4 комірки, або 32 біта.Процес запису абсолютно не відрізняється від представленого вище. Так що ми просто приведемо діапазон чисел, які можуть зберігатися в даному типі. Х мах =2147483 647. Х min = - 2147483 648. Даних значень в більшості випадків досить для того, щоб записувати та проводити операції з даними. Подання дійсних чисел у комп'ютері має свої переваги і недоліки. З одного боку, дана методика дозволяє простіше проводити операції між цілочисельними значеннями, що значно прискорює роботу процесора. З іншого боку, цього діапазону недостатньо для вирішення більшості завдань економіки, фізики, арифметики та інших наук. Тому тепер ми розглянемо чергову методику для сверхвеличин.
Плаваюча кома
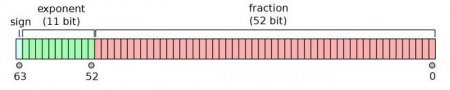
Це останнє, що вам необхідно знати про представлення чисел в комп'ютері. Оскільки при запису дробів виникає проблема визначення положення коми в них, для розміщення подібних цифр в комп'ютері використовується експоненціальна форма. Будь-яке число може бути представлене в наступному вигляді Х = m * р п . Де m – це мантиса числа, р – основа системи числення і п – порядок числа. Для стандартизації запису чисел з плаваючою комою використовується наступна умова, згідно з яким модуль мантиси повинен бути більше або дорівнює 1/п і менше 1. Нехай нам дано число 66666. Наведемо його до експоненційної формі. Вийде Х = 066666 * 10 3 . Р = 10 і п = 3. На зберігання значень з плаваючою комою зазвичай виділяється 4 або 8 байт (32 або 64 біта). В першому випадку це називається числом звичайної точності, а в другому – подвійної точності. З 4 байт, виділених під зберігання цифр, 1 (8 розрядів) віддається під дані про порядок та його знаку, а 3 байти (24 розряду) йдуть на зберігання мантиси і її знака за тими ж принципами, що і для цілочислових значень. Знаючи це, ми можемо провести нехитрі розрахунки. Максимальне значення п = 1111111 2 = 127 10 . Виходячи з нього, ми можемо отримати максимальний розмір числа, яке може зберігатися в пам'яті комп'ютера. Х=2 127 . Тепер ми можемо обчислити максимально можливу мантиссу. Вона буде дорівнює 2 23 – 1 >= 2 23 = 2 (10 x 23) >= 1000 23 = 10 (3 x 23) >= 10 7 . В результаті, ми отримали наближене значення. Якщо тепер ми об'єднаємо обидва розрахунку, то отримаємо значення, яке може бути записано без втрат в 4 байти пам'яті. Воно буде дорівнює Х = 1701411 * 10 38 . Інші цифри були відкинуті, оскільки саме таку точність дозволяє мати даний спосіб запису.Подвійна точність
Оскільки всі обчислення були розписані і пояснені в попередньому пункті, тут ми розповімо все дуже коротко. Для чисел з подвійною точністю зазвичай виділяється 11 розрядів для порядку і його знака, а також 53 розряду для мантиси. П = 1111111111 2 = 1023 10 . М = 2 52 -1 = 2 (10*5.2) = 1000 5.2 = 10 15.6 . Округляємо в більшу сторону і отримуємо максимальне число Х = 2 1023 з точністю до "м". Сподіваємося, що інформація про представлення цілих і дійсних чисел в комп'ютері, яку ми надали, стане в нагоді вам у навчанні і буде хоч трохи зрозуміліше, ніж те, що зазвичай пишуть у підручниках.Схожі добрі поради по темі

Так ось що робить ця кнопка на клавіатурі! Знати б раніше ...
Мало хто знає, для чого на клавіатурі потрібна гаряча клавіша Win . А адже її використання значно може спростити повсякденну роботу на комп'ютері. У

Чому двійкове кодування є універсальним? Методи програмування
Комп'ютер обробляє велику кількість інформації. Аудіо-файли, картинки, тексти – все це необхідно відтворити або вивести на екран. Чому двійкове

Лаунчер для Android: вибір нової оболонки для девайса
Лаунчер для Android - це вид системної утиліти. Його ще називають лончером (проблема транслітерації з англійської мови). Він являє собою інтерфейс,

Округлення чисел: цілі і дроби
Тему про округлення чисел проходять ще в початковій школі. Це вміння так чи інакше постійно потрібно в побуті. Люди навіть не помічають, як
Комплексні числа та дії над ними
Комплексні числа не є числами в елементарному значенні цього слова, що застосовуються при підрахунках і вимірюваннях, а є математичними об'єктами,

Лікнеп: як оновити драйвера
Для коректної роботи комп'ютера або ноутбука необхідно періодично проводити оновлення його програмного забезпечення, в тому числі і драйверів для