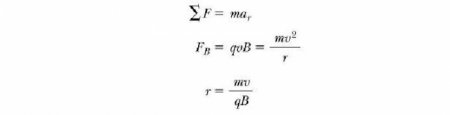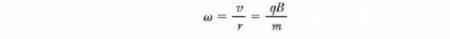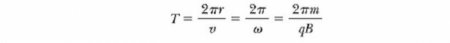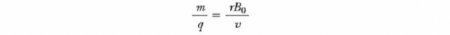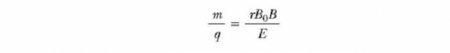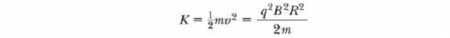Рух зарядженої частинки в магнітному полі: формули. Рух заряджених частинок в однорідному магнітному полі
Як відомо, електричне поле прийнято характеризувати величиною сили, з якою воно діє на пробний одиничний електричний заряд. Магнітне поле традиційно характеризують силою, з якою воно діє на провідник з «поодиноким» струмом. Однак при його протіканні відбувається впорядкований рух заряджених частинок у магнітному полі. Тому ми можемо визначити магнітне поле B у якійсь точці простору з точки зору магнітної сили F B , яку поле має на частку при її русі в ньому зі швидкістю v.
Величина F B магнітної сили, що діє на частинку пропорційна заряду q і швидкості v частинки. Якщо рух зарядженої частинки в магнітному полі відбувається паралельно вектору поля, то сила, що діє на неї, дорівнює нулю. Коли вектор швидкості частинки складає довільний Кут /= 0 з магнітним полем, то сила діє в напрямку, перпендикулярному до v і B; тобто, F B перпендикулярна площині, утвореної v і B (см. рис. нижче). Величина і напрям F B залежить від швидкості частинки і від величини і напрямку магнітного поля B. Напрям сили, що діє на позитивний заряд, протилежно напрямку такої ж сили, що діє на негативний заряд, що рухається в ту ж сторону. Величина магнітної сили, що діє на рухому частку, пропорційна sin кута між векторами v і B.
Коли відбувається рух зарядженої частинки в магнітному полі, сила Лоренца F B при позитивному q спрямована вздовж векторного добутку v x B. Воно за визначенням перпендикулярно як v, так і B. Вважаємо це рівняння робочим визначенням магнітного поля в деякій точці в просторі. Тобто воно визначається в термінах сили, що діє на частинку при її русі. Таким чином, рух зарядженої частинки в магнітному полі коротко можна визначити як переміщення під дією цієї сили. Заряд, що рухається зі швидкістю v у присутності електричного поля E, так і магнітного B, відчуває дію як електричної сили qE, так і магнітної qv х Ст. Повне прикладена до нього вплив одно F Л = qE + qv х Ст. Його прийнято називати так: повна сила Лоренца.
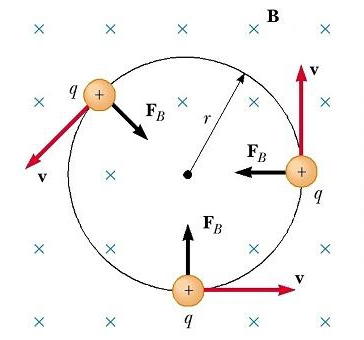 Рух зарядженої частинки в магнітному полі по колу відбувається тому, що магнітна сила F B спрямована під прямим кутом до v і B і має постійну величину qvB. Оскільки сила відхиляє частинки, напрямки v і F B змінюються безперервно, як показано на рисунку. Так як F B завжди спрямована до центра окружності, вона змінює лише напрям v, а не її величину. Як показано на малюнку, рух позитивно зарядженої частинки в магнітному полі відбувається проти годинникової стрілки. Якщо q буде негативним, то обертання відбудеться за годинниковою стрілкою.
Рух зарядженої частинки в магнітному полі по колу відбувається тому, що магнітна сила F B спрямована під прямим кутом до v і B і має постійну величину qvB. Оскільки сила відхиляє частинки, напрямки v і F B змінюються безперервно, як показано на рисунку. Так як F B завжди спрямована до центра окружності, вона змінює лише напрям v, а не її величину. Як показано на малюнку, рух позитивно зарядженої частинки в магнітному полі відбувається проти годинникової стрілки. Якщо q буде негативним, то обертання відбудеться за годинниковою стрілкою. 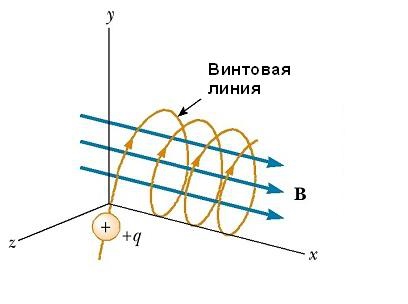
 Заряджена частинка стартує з одного кінця гвинтовій лінії, накрученою вздовж силових ліній, і рухається вздовж неї, поки не досягне іншого кінця, де вона повертає свій шлях назад. Ця конфігурація відома як "магнітна пляшка", оскільки заряджені частинки можуть бути захоплені в неї. Вона була використана, щоб обмежити плазму, газ, що складається з іонів та електронів. Така схема плазмового ув'язнення може виконувати ключову роль у контролі ядерного синтезу, процесі, який представить нам майже невичерпне джерело енергії. На жаль, "магнітна пляшка" має свої проблеми. Якщо в пастці велике число частинок, зіткнення між ними викликають витік із системи.
Заряджена частинка стартує з одного кінця гвинтовій лінії, накрученою вздовж силових ліній, і рухається вздовж неї, поки не досягне іншого кінця, де вона повертає свій шлях назад. Ця конфігурація відома як "магнітна пляшка", оскільки заряджені частинки можуть бути захоплені в неї. Вона була використана, щоб обмежити плазму, газ, що складається з іонів та електронів. Така схема плазмового ув'язнення може виконувати ключову роль у контролі ядерного синтезу, процесі, який представить нам майже невичерпне джерело енергії. На жаль, "магнітна пляшка" має свої проблеми. Якщо в пастці велике число частинок, зіткнення між ними викликають витік із системи. 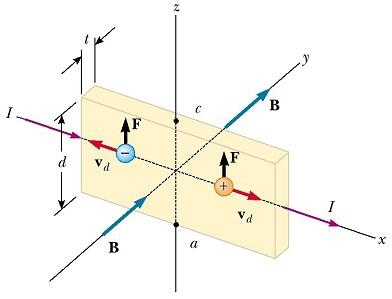 Однорідне поле B докладено у напрямі. Якщо носіями заряду є електрони, що рухаються вздовж осі х із швидкістю дрейфу v d , то вони відчувають спрямовану вгору (з урахуванням від'ємного q) магнітну силу F B = qv d х B, відхиляються вгору і накопичуються на верхньому краю плоского провідника, в результаті чого з'являється надлишок позитивного заряду на нижньому краю. Це накопичення заряду на краях збільшується до тих пір, поки електрична сила, що з'явилася в результаті поділу зарядів, не врівноважує магнітну силу, діючу на носії. Коли ця рівновага буде досягнута, електрони більше не відхиляються вгору. Чутливий вольтметр або потенціометр, підключений до верхній і нижній гранях провідника, може виміряти різницю потенціалів, відому як ЕРС Холла.
Однорідне поле B докладено у напрямі. Якщо носіями заряду є електрони, що рухаються вздовж осі х із швидкістю дрейфу v d , то вони відчувають спрямовану вгору (з урахуванням від'ємного q) магнітну силу F B = qv d х B, відхиляються вгору і накопичуються на верхньому краю плоского провідника, в результаті чого з'являється надлишок позитивного заряду на нижньому краю. Це накопичення заряду на краях збільшується до тих пір, поки електрична сила, що з'явилася в результаті поділу зарядів, не врівноважує магнітну силу, діючу на носії. Коли ця рівновага буде досягнута, електрони більше не відхиляються вгору. Чутливий вольтметр або потенціометр, підключений до верхній і нижній гранях провідника, може виміряти різницю потенціалів, відому як ЕРС Холла.
Загальні властивості магнітної сили
Експерименти, в яких спостерігалося рух заряджених частинок в магнітному полі, дають такі результати:Сила Лоренца
Ми можемо підсумувати вищеперелічені спостереження шляхом запису магнітної сили у вигляді F B = qv х B.Коли відбувається рух зарядженої частинки в магнітному полі, сила Лоренца F B при позитивному q спрямована вздовж векторного добутку v x B. Воно за визначенням перпендикулярно як v, так і B. Вважаємо це рівняння робочим визначенням магнітного поля в деякій точці в просторі. Тобто воно визначається в термінах сили, що діє на частинку при її русі. Таким чином, рух зарядженої частинки в магнітному полі коротко можна визначити як переміщення під дією цієї сили. Заряд, що рухається зі швидкістю v у присутності електричного поля E, так і магнітного B, відчуває дію як електричної сили qE, так і магнітної qv х Ст. Повне прикладена до нього вплив одно F Л = qE + qv х Ст. Його прийнято називати так: повна сила Лоренца.
Рух заряджених частинок в однорідному магнітному полі
Розглянемо тепер приватний випадок позитивно зарядженої частинки, що рухається в однорідному полі, з початковим вектором швидкості, перпендикулярний йому. Припустимо, що вектор B поля спрямований за сторінку. Малюнок нижче показує, що частинка рухається по колу в площині, перпендикулярній до B.
Динаміка кругового руху частинки
Які параметри характеризують вищеописане рух зарядженої частинки в магнітному полі? Формули для їх визначення ми можемо отримати, якщо візьмемо попереднє рівняння і приравняем F B відцентровій силі, необхідної для збереження кругової траєкторії руху: Тобто радіус кола пропорційний імпульсу mv частинки і обернено пропорційний величині її заряду і величиною магнітного поля. Кутова швидкість частинки Період, з яким відбувається рух зарядженої частинки в магнітному полі по колу, дорівнює довжині кола, розділеного на її лінійну швидкість: Ці результати показують, що кутова швидкість частинки і період кругового руху не залежить від лінійної швидкості або від радіуса орбіти. Кутову швидкість часто називають циклотронне частотою (кругової), тому що заряджені частинки циркулюють з нею в типі прискорювача під назвою циклотрон.Рух частинки під кутом до вектора магнітного поля
Якщо вектор швидкості v частинки утворює деякий довільний кут по відношенню до вектора B, то її траєкторія є гвинтовою лінією. Наприклад, якщо однорідне поле буде направлено вздовж осі х, як показано на малюнку нижче, то не існує ніякої компоненти магнітної сили F B в цьому напрямку. В результаті складова прискорення a x = 0 і х-складова швидкості руху частинки є постійною. Однак магнітна сила F B = qv х В викликає зміну в часі компонентів швидкості v y і v z . В результаті має місце рух зарядженої частинки в магнітному полі по гвинтовій лінії, вісь якої паралельна магнітному полю. Проекція траєкторії на площині yz (якщо дивитися вздовж осі х) являє собою коло. Проекції її на площині ху і xz є синусоидами! Рівняння руху залишаються такими ж, як і при круговій траєкторії, за умови, що v замінюється на = ( у 2 + z 2 ).
Неоднорідне магнітне поле: як у ньому рухаються частинки
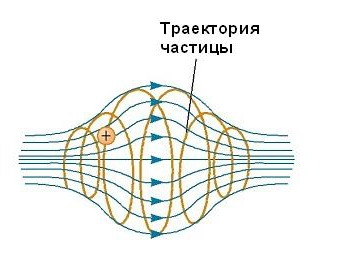
Рух зарядженої частинки в магнітному полі, що є неоднорідним, відбувається по складних траєкторіях. Так, в поле, величина якого посилюється по краях області його існування і послаблюється в її середині, як, наприклад, показано на малюнку нижче, частинка може коливатися вперед і назад між кінцевими точками.
Як Земля впливає на рух космічних частинок
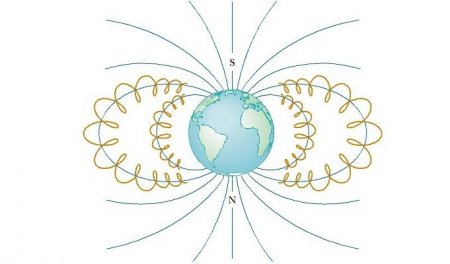
Навколоземні пояси Ван Аллена складаються із заряджених частинок (в основному електронів і протонів), що оточують Землю у формі тороїдальних областей (см. рис. нижче). Рух зарядженої частинки в магнітному полі Землі відбувається по спіралі навколо силових ліній від полюса до полюса, покриваючи відстань у кілька секунд. Ці частинки йдуть в основному від Сонця, але деякі приходять від зірок і інших небесних об'єктів. З цієї причини вони називаються космічними променями. Більшість їх відхиляється магнітним полем Землі і ніколи не досягає атмосфери. Тим не менш, деякі з частинок потрапляють в пастку, саме вони складають пояси Ван Аллена. Коли вони знаходяться над полюсами, іноді відбуваються зіткнення їх з атомами в атмосфері, в результаті чого останні випромінюють видиме світло. Так виникають красиві Полярні сяйва в Північному і Південному півкулях. Вони, як правило, відбуваються в полярних регіонах, тому що саме тут пояси Ван Аллена розташовані найближче до поверхні Землі. Іноді, однак, сонячна активність викликає більшу кількість заряджених частинок, що входять в ці пояси, і значно спотворює нормальні силові лінії магнітного поля, пов'язані з Землею. У цих ситуаціях полярне сяйво можна іноді побачити в більш низьких широтах.Селектор швидкостей
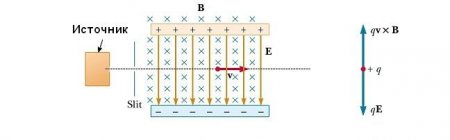
У багатьох експериментах, в яких відбувається рух заряджених частинок в однорідному магнітному полі, важливо, щоб всі частинки рухалися з практично однаковою швидкістю. Це може бути досягнуто шляхом застосування комбінації електричного поля і магнітного поля, орієнтованого так, як показано на малюнку нижче. Однорідне електричне поле спрямоване вертикально вниз (в площині сторінки), а таке ж магнітне поле докладено в напрямку, перпендикулярному до електричного (за сторінку). Для позитивного q магнітна сила F B =qv х У спрямована вгору, а електрична сила qE – вниз. Коли величини двох полів вибрані так, що qE = qvB, то частинка рухається по прямій горизонтальній лінії через область поля. З виразу qE = qvB ми знаходимо, що тільки частинки, що мають швидкість v=E/B, проходять без відхилення через взаємно перпендикулярні електричне і магнітне поля. Сила F B , що діє на частинки, які рухаються зі швидкістю більшою, ніж v=E/B, виявляється більше електричної, і вони відхиляються вгору. Ті ж з них, які рухаються з меншою швидкістю, відхиляються вниз.Мас-спектрометр
Цей прилад розділяє іони у відповідності із співвідношенням їх маси до заряду. За однією з версій цього пристрою, відомого як мас-спектрометр Бэйнбриджа, пучок іонів проходить спочатку через селектор швидкостей і потім надходить у друге поле B 0 також однорідне і має той же напрямок, що і поле селектора (см. рис. нижче). Після входу в нього рух зарядженої частинки в магнітному полі відбувається по півколу радіуса r перед ударом в фотопластинку Р. Якщо заряджені іони позитивно, промінь відхиляється вгору, як показано на рисунку. Якщо іони заряджені негативно, промінь буде відхилятися вниз. З виразу для радіуса кругової траєкторії частинки, ми можемо знайти відношення m/q і потім, використовуючи рівняння v=E/B, ми знаходимо, що Таким чином, ми можемо визначити m/q шляхом вимірювання радіуса кривизни, знаючи поля величин B, B 0 і E. На практиці, так зазвичай вимірює маси різних ізотопів даного іона, оскільки всі вони несуть один заряд q. Таким чином, відношення мас може бути визначено, навіть якщо q невідомо. Різновид цього методу була використана Дж. Дж. Томсон (1856-1940) в 1897 році для вимірювання відношення е/m е для електронів.Циклотрон
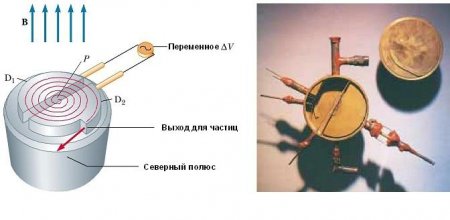
Він може прискорити заряджені частинки до дуже високих швидкостей. І електричні і магнітні сили відіграють тут ключову роль. Отримані високоенергетичні частинки використовуються для бомбардування атомних ядер, і тим самим роблять ядерні реакції, представляють інтерес для дослідників. Ряд лікарень використовує циклотронное обладнання для одержання радіоактивних речовин для діагностики і лікування. Схематичне зображення циклотрона показаний на рис. нижче. Частинки рухаються всередині двох напівциліндричних контейнерів D 1 і D 2 званих дуантами. Високочастотна змінна різниця потенціалів прикладена до дуантам, розділених зазором, а однорідне магнітне поле направлене вздовж осі циклотрона (південний полюс його джерела на рис. не показаний). Позитивний іон, випущений з джерела в точці Р поблизу центру пристрою в першому дуанте, переміщається по напівкруглої траєкторії (показана пунктирною червоною лінією на малюнку) і прибуває назад в щілину в момент часу Т /2 де Т - час одного повного обороту всередині двох дуантов. Частота прикладеної різниці потенціалів регулюється таким чином, що полярність дуантов змінюється на зворотну в той момент часу, коли іон виходить з одного дуанта. Якщо прикладена різниця потенціалів регулюється таким чином, що в цей момент D 2 одержує більш низький електричний потенціал, ніж D 1 на величину qV, то іон прискорюється у зазорі перед входом в D 2 і його кінетичної енергії збільшується на величину qV. Потім він рухається навколо D 2 за напівкруглої траєкторії більшого радіуса (тому що його швидкість збільшилася). Через деякий час T /2 він знову надходить у зазор між дуантами. До цього моменту полярність дуантов знову змінюється, і йону дається ще один "удар" через зазор. Рух зарядженої частинки в магнітному полі по спіралі триває, так що при кожному проході одного дуанта іон отримує додаткову кінетичну енергію, рівну qV. Коли радіус його траєкторії стає близьким до радіусу дуантов, іон залишає систему через вихідну щілину. Важливо відзначити, що робота циклотрона заснована на тому, що Т не залежить від швидкості іона і радіуса кругової траєкторії. Ми можемо отримати вираз для кінетичної енергії іона, коли він виходить з циклотрона в залежності від радіуса R дуантов. Ми знаємо, що швидкість кругового руху частинки - = qBR /m. Отже, її кінетична енергія Коли енергії іонів в циклотрон перевищує близько 20 Мев, в гру вступають релятивістські ефекти. Ми відзначаємо, що T збільшується, і що рухомі іони не залишаються у фазі з прикладеної різниці потенціалів. Деякі корисні вирішують цю проблему, змінюючи період прикладається різниці потенціалів, так що вона залишається в фазі з рухомими іонами.Ефект Холла
Коли провідник зі струмом поміщається в магнітне поле, то додаткова різниця потенціалів створюється в напрямку, перпендикулярному до напрямку струму і магнітного поля. Це явище, вперше спостерігається Едвіном Холом (1855-1938) в 1879 році, відоме як ефект Холу. Він завжди спостерігається, коли відбувається рух зарядженої частинки в магнітному полі. Це призводить до відхилення носіїв заряду на одній стороні провідника в результаті магнітної сили, яку вони відчувають. Ефект Холла дає інформацію про знак носіїв заряду і їх щільності, він також може бути використаний для вимірювання величини магнітних полів. Пристрій для спостереження ефекту Холла складається з плоского провідника зі струмом I у напрямку х, як показано на малюнку нижче.
Схожі добрі поради по темі

Провідник в електростатичному полі. Провідники, напівпровідники, діелектрики
Речовиною, що мають вільні частинки з зарядом, що рухаються по тілу за рахунок діючого електричного поля впорядковано, називають провідник в
Рухомий електричний заряд створює яке поле?
Те, що рухомий електричний заряд створює навколо себе, є більш складним, ніж те, що властиво заряду, що знаходиться у нерухомому стані. В ефірі, де

Рухомий електричний заряд від Галактики до Землі
Рухомий електричний заряд лежить в основі багатьох явищ, що відбуваються в природі. Наприклад, безліч частинок, заряджених високою енергією, постійно
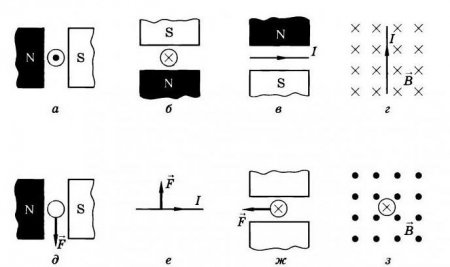
Що таке сила Ампера?
Сила Ампера є важливою теоретичної складової для тих людей, які працюють з електрично розсувними частинами. Про неї і піде мова.

Що таке маса електрона?
Відомо, що електрони мають негативний заряд. Але яким чином можна переконатися в тому, що маса електрона і його заряд постійні для всіх цих частинок?

Магнітні поля і індукція магнітного поля
В даній статті розповідається про магнітних полях та їх властивості. Особливу увагу приділено магнітної індукції, так як це основна характеристика