Метод кінцевих елементів виник як один із прийомів дослідження різних конструкцій. В даний час він повсюдно визнано як загальний спосіб вирішення широкого кола завдань в різних областях техніки.
Визначення
Інженерний аналіз методом кінцевих елементів полягає в апроксимації суцільного середовища з нескінченно великими числами ступенів свободи сукупністю елементів (подобластей), що мають кінцеві числа ступенів свободи. Між цими елементами встановлюється взаємозв'язок. Визнання методу пояснюється простотою його математичної форми і фізичного тлумачення.
Застосування в механіці
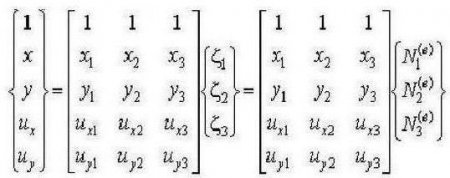
Метод кінцевих елементів в механіці руйнування і в задачах будівельної механіки виражається як співвідношення МСЕ у формі переміщень. Спочатку задаються в межах кожного елемента так звані функції форми. Вони визначають переміщення у внутрішній області елемента по переміщенню у вузлах. Останні – це точки, де поєднуються кінцеві елементи. Невідомими МСЕ є можливі і незалежні переміщення вузлів звичайно елементної моделі (КЕМ). Таким чином, КЕМ конструкції являє собою систему закріплених вузлів. Додаткові зв'язку співвідносяться з напрямком можливих переміщень вузлів.
Суть методу
По своїй суті елементна модель конструкції аналогічна основній системі класичного методу переміщень, що застосовується при розрахунку стержневих систем. Для досягнення сприйнятливою точності результатів розрахунків за методом кінцевих елементів доводиться зменшувати розміри елементів, збільшуючи тим самим точність апроксимації геометричних характеристик і функцій переміщень в межах кінцевого елемента.
КЕМ складних конструкцій досягають сотень і навіть мільйонів ступенів свободи, а тому метод кінцевих елементів в техніці є машинно-орієнтованим, реалізація якого можлива тільки за допомогою комп'ютерів.
Практична реалізація
Для застосування МКЕ на практиці необхідно розбиратися не тільки в теорії механіки, але і володіти знаннями в області програмування. Застосування методу кінцевих елементів часто будується на базі варіаційних принципів механіки, в основі яких закладені два фундаментальних скаляр: потенційна і кінетична енергія пружної конструкції. Визначення цих скаляров, незалежних від обраної системи координат, дозволяє записувати співвідношення МСЕ в інваріантної формі.
Для забезпечення зручності програмування співвідношення МСЕ записуються в компактній матричної, або тензорною формі. На сьогодні моделювання методом кінцевих елементів досить повно математично обґрунтовано, створені високоефективні програмні продукти, які весь час вдосконалюються разом із засобами програмування.
Навчально-обчислювальні програми
Технічний прогрес, особливо в області ЕОМ, істотно змінив погляди на постановку та вирішення інженерних завдань. Побудова розрахункової моделі тісно пов'язане з процесом обчислень, і розділити ці два етапи на шляху отримання практичних результатів майже неможливо. Метод кінцевих елементів широко застосовується в інженерній практиці, що також сприяло включенню його в навчальні програми вузів. МСЕ надає способи побудови математичної моделі досліджуваного явища, виходячи з його фізичної сутності. Перші підручники по МКЕ були написані складною мовою, але незабаром була спрощена методика викладання завдяки впровадженню спеціалізованих програм. Наприклад, добре себе зарекомендував програмний комплекс «Асистент». Він дозволяє перевірити знання студентів в інтерактивному режимі і сприяє розвитку навичок роботи з програмними продуктами при вирішенні практичних завдань.
Розрахунок лінійних деформацій
Сьогодні основи методу скінченних елементів базуються на тому, що величини і поняття, йому притаманні, не вводяться заздалегідь, а випливають із істоти задачі будівельної механіки. Коло проблем, які можна вирішувати за допомогою МСЕ, практично необмежений. Розглянемо для прикладу завдання по розрахунку лінійної деформації пружних конструкцій від дії статичних навантажень.
Англійський фізик Р. Гук провів дослідження деформацій центрально-навантажених стрижнів, виконаних з різних пружних матеріалів, під дією статичної сили: =Pl/EA. Він також встановив залежність між величинами, що визначають цей процес: =E, де деформація виражена співвідношенням =/l, напруга позначено як =P/A (тут A – площа перерізу стрижня). Коефіцієнт пропорційності E визначає пружні характеристики матеріалу і має фізичну суть – напруга, відповідне одиничної деформації.
Вплив статичної сили
Статично діюча сила зростає у часі поступово (G>=P>=0). Переміщення, які вона породжує, теж ростуть поступово, без прискорень.
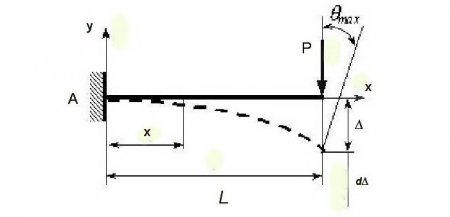
Аналіз методом кінцевих елементів дозволяє визначити вплив статичної сили на переміщення, враховуючи, що ці показники змінюються. Зростання (приросту) сили на нескінченно малу величину dP відповідає зростання (приріст) переміщення d. Робота сили (P+P) на переміщення d має значення dA=(P+P)xd. Остаточне значення роботи сили визначається за формулою A=Pd. Введемо залежність між разномерними величинами під знаком інтеграла =P, де – коефіцієнт податливості, який виражає фізичну сутність переміщення точки, до якої додана одинична сила, в напрямку цієї сили. Співвідношення =P встановлює одиницю вимірювання (м/М). Звідси випливає, що d=dP. Коефіцієнта податливості відповідає інша важлива характеристика конструкції – коефіцієнт жорсткості k=l/(н/м), який визначає силу, що викликає одиничне переміщення конструкції в напрямку цієї сили. З урахуванням всіх характеристик і коефіцієнтів підсумкове рівняння приймає вигляд: A=PdP = x(P 2 /2)=(G)/2. Отримана формула Клапейрона, яка визначає дійсну роботу статично діючої сили на переміщення, нею ж породжене в пружному тілі. За цією методикою розраховуються й інші чисельні методи.
Метод кінцевих елементів для стрижневих систем
Стрижень є просторовим тілом, два якого розміру, ширина і висота, набагато менше довжини. Це дає можливість розглядати його фізичну модель у вигляді лінії, що проходить через центри перерізів. Якщо зовнішні сили, прикладені до стрижня, розташовані в одній площині з його моделлю, то можна вважати, що деформації його відбуваються в цій же площині.
З математичної точки зору геометричні характеристики переміщення і напруги в межах стрижня є функціями одного аргументу. Співвідношення теорії пружності базуються на гіпотезі плоских перерізів стержня. Зв'язок між деформаціями і напруженнями відповідає лінійному закону Гука. В кожному перерізі стрижня проявляються три площини переміщення:
координата u – поздовжня сила; координата w – прогин; координата – кут повороту. При цьому поздовжня u і прогин w незалежні, а кут повороту виражається формулою =dw/dx, де dw – величина прогину після впливу на стрижень зовнішньої сили, dx – ділянка прогину (визначається значенням w+dw). Для нескінченно малої величини стрижня dx діє співвідношення dx=dxP. Потенційну енергію деформації стрижня природно обчислювати в локальній системі координат, вісь x якої збігається з віссю стрижня, а вісь y перпендикулярна осі стрижня: U= 1/2 Nxdu+ 1/2 Mxd= 1/2 Nx(du/dx)dx+ 1/2 Mx(d2w/dx2)dx.
Изопараметрический підхід в МСЕ
Розглянемо застосування методу кінцевих елементів в системі изопараметрической кінцевих елементів плоско-напруженої конструкції. Процес створення звісно елементної моделі конструкцій складається з декількох етапів, першим з яких є побудова сітки скінченних елементів (СЕ), вибір глобальної системи координат відносно цілої конструкції та локальної системи, пов'язаної з кінцевим елементом. Відповідальним етапом є визначення функцій форми, які забезпечують визначення переміщень в межах кінцевого елемента з-за переміщення його вузлів. Є різні способи побудови функцій форми, але вони повинні забезпечити виконання кількох умов щодо апроксимації функцій переміщень.
Виконання умов нерозривності переміщень не тільки у вузлах скінченних елементів, але і на їх межах. Забезпечення збереження похідних від функцій переміщень, які відносяться до пружному потенціалу. Рух переміщення кінцевого елемента як жорсткого цілого. Це означає, що при зміщенні елемента як твердого тіла компоненти вектора деформацій дорівнюють нулю. Проблеми і рішення
Теорія методів кінцевих елементів свідчить, що співвідношення МСЕ формуються в локальній системі координат. Тому перераховані вимоги щодо функцій форми виконуються автоматично, якщо осі локальної системи орієнтовані по сторонах кінцевого елемента. Такі випадки мають місце для кінцевих елементів стержневих конструкцій, прямокутних стінових панелей, прямокутних плит. Але на практиці зустрічаються конструкції з контуром довільного визначення. У цьому випадку доводиться виконувати перетворення для апроксимації переміщень в глобальній системі координат, що призводить до розривів переміщень на кордонах кінцевих елементів і, як наслідок, – до втрати точності наближених розрахунків. Виникла ідея відобразити плоский чотирикутний кінцевий елемент загального виду на квадрат з локальною системою координат, початок якої знаходиться в центрі цієї фігури, і осями, орієнтованими по його сторонах. Для подальшого використання скінченних елементів у формі квадрата необхідно встановити взаємно однозначну зв'язок між локальними координатами довільного чотирикутного СЕ та локальною системою координат СЕ у формі квадрата. Адже для квадратного кінцевого елемента функції форми будуються досить просто.
Метод кінцевих елементів для розрахунку пластин
Пластина – це вставка або циліндричне тіло, висота якого значно менше розмірів в плані. Розмір по висоті називається товщиною пластини. Площина, яка ділить висоту пластини навпіл, називається серединної або базовою площиною. Лінія перетину бічної поверхні з серединною площиною називається контуром пластини. Тонкою вважається пластина, для якої відношення товщини до меншого розміру в плані знаходиться в межах h<=L/5 де h – товщина пластини, L – її ширина. Пластина вважається твердою, якщо під дією поперечного навантаження найбільший її прогин при деформації не перевищує 1/5 товщини. При розрахунку методом СЕ спочатку вводять систему координат: X 1 , X 2 і X 3 . Початку осей X 1 і X 2 розташовані в серединній площині. Вісь X 3 орієнтують по нормалі до серединної площини. Розрахунки зазвичай зводяться до обчислення переміщення (зрушення) пластини в якійсь точці під впливом навантажень (сил). У довільній точці пластини, яка розглядається як трьохвимірне тіло, проявляються три напрямки переміщення: U 1 , U 2 , U 3 . Визначальним є переміщення по нормалі до серединної площини, яке називається прогином і позначається буквою W. Розрахунки вважаються виконаними, якщо від заданого навантаження (а це зазвичай рівномірно розподілена, спрямована до поверхні) встановлений спосіб обчислення переміщень U і зсуву W в довільній точці пластини. Співвідношення МСЕ будуються на основі положень технічної теорії пружності, запропонованих фізиком Кирхгофом.
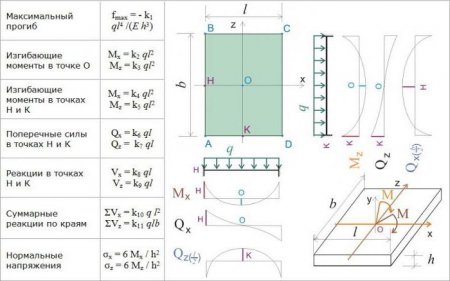
Гіпотези Кірхгофа
Метод кінцевих елементів багато в чому ґрунтується на гіпотезах, сформульованих у 1845 Р. німецьким фізиком Киргофом. Гіпотеза прямих нормалей стверджує, що будь-яка пряма лінія, нормальна до серединної площини недеформованою пластини, залишається прямою і нормального до серединної поверхні деформованої пластини, а довжина прямої лінії не змінюється. Суть її полягає у відсутності зсуву між шарами по товщині пластини. Якщо осі декартових координат розміщені так, що площині X 1 , X 2 збігаються з серединною площиною, то з першої частини гіпотези випливають наступні рівності: y 13 =0 y 23 =0. Гіпотеза про незмінність довжини прямої лінії передбачає, що лінійна деформація в напрямку осі X 3 дорівнює нулю: 33 =0. Гіпотеза про відсутність тиску між шарами пластини, паралельними серединної поверхні, передбачає, що напруженнями 33 у порівнянні з напруженнями 11 і 22 можна знехтувати, тобто 33 =0. Гіпотеза про недеформируемости серединної площини припускає, що в серединній площині пластини відсутні деформації розтягування, стиснення та зсуву. Тобто серединна площина є нейтральною. Так що в ній переміщення U 1 =U 2 =0.
Висновок
Метод кінцевих елементів, широко застосовуваний у будівництві та механіки, що дозволяє розраховувати зміщення різних елементів, що піддаються певним навантаженням. Система, сформульована ще в 1936 році радянськими вченими, почала широко застосовуватися лише через десятиліття, так як вимагала великого об'єму розрахунків. З впровадженням ЕОМ ця задача спростилася.
 Англійський фізик Р. Гук провів дослідження деформацій центрально-навантажених стрижнів, виконаних з різних пружних матеріалів, під дією статичної сили: =Pl/EA. Він також встановив залежність між величинами, що визначають цей процес: =E, де деформація виражена співвідношенням =/l, напруга позначено як =P/A (тут A – площа перерізу стрижня). Коефіцієнт пропорційності E визначає пружні характеристики матеріалу і має фізичну суть – напруга, відповідне одиничної деформації.
Англійський фізик Р. Гук провів дослідження деформацій центрально-навантажених стрижнів, виконаних з різних пружних матеріалів, під дією статичної сили: =Pl/EA. Він також встановив залежність між величинами, що визначають цей процес: =E, де деформація виражена співвідношенням =/l, напруга позначено як =P/A (тут A – площа перерізу стрижня). Коефіцієнт пропорційності E визначає пружні характеристики матеріалу і має фізичну суть – напруга, відповідне одиничної деформації. 





