Вернутися назад
Друкувати
Комплексні числа та дії над ними
Комплексні числа , у традиційному розумінні цього слова, не є числами, що застосовуються при підрахунках і вимірюваннях, а є математичними об'єктами, які визначаються представленими нижче властивостями. 
Використовують 3 форми комплексного числа: алгебраїчну, показову, тригонометрическую.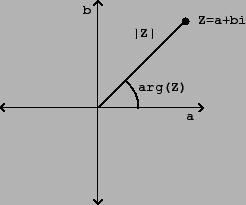 
Рівними вважаються комплексні числа, коли еквівалентні їх і дійсні та уявні частини. Рівним нулю вважається комплексне число, якщо його частини, дійсна та уявна, дорівнюють нулю. 
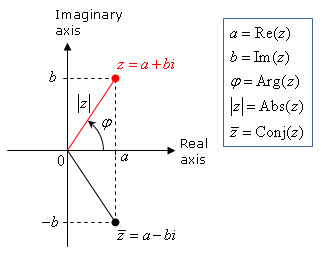Комплексне Число + i можна записати так: =k(cos+isin), де k 2 = 2 + 2 . Це вираз - форма запису комплексних чисел, яка носить назву тригонометричної. Модуль комплексного числа - дійсне число k , а кут , що вимірюється в радіанах - його аргументом. Якщо комплексне число дорівнює нулю, то модуль його позитивний; якщо ж =0 інакше кажучи ==0 , то й модуль його дорівнює нулю. Модуль визначений однозначно. Твором тригонометричних комплексних чисел є модуль комплексного числа, який еквівалентний добутку множників, вірніше, їх модулів, а аргумент еквівалентний сумі аргументів множників:
1 2 =k 1 k 2 [cos(β1+β2)+isin(β1+β2)]. Приватним тригонометричних комплексних чисел, які не дорівнюють нулю, є комплексне число, модуль якого еквівалентний приватному діленого і дільника (їх модулів), а аргумент еквівалентний різниці аргументів діленого і дільника: 1 / 2 =k 1 /k 2 [cos(β1-β2)+isin(β1-β2)].
Алгебраїчна Форма
Комплексні числа позначають виразом + i, де є дійсними і , а символ i , визначається умовою i 2 - 1 - уявна одиниця. Відповідно число комплексне + i ділиться на дійсну і уявну частину. Для зручності зображують його однією буквою (наприклад ): = + i . Частини комплексного числа = + i , дійсну та уявну, позначають = Re, = It відповідно.Арифметичні дії
Додавання Сумою комплексних чисел називають комплексне число, дійсна частина якого еквівалентна сумі дійсних частин, а уявна еквівалентна сумі уявних частин: =( 1 + 2 )+( 1 + 2 )i. Кажуть що в числі комплексному знайшли в результаті додавання комплексних чисел : = 1 + 2. Комплексні 1 і 2 іменують доданками. Закони операції додавання: 1) закон асоціативності; 2) закон комутативності . Комплексне Число --bi називають комплексного числа +i протилежним. Сума протилежних комплексних чисел дорівнює нулю. Різниця Різницею комплексних чисел називають число комплексне дорівнює сумі числа 1 і числа протилежної 2 : = 1 +(- 2 )=( 1 - 2 )+( 1 - 2 )i. Про числі комплексному кажуть, що його знайшли в результаті віднімання 2 і 1 (комплексних чисел), і записують: = 2 - 1 . Твір Добутком чисел комплексних є комплексне число: =( 1 2 - 1 2 )+( 1 1 + 2 1 )i. Про числі комплексному кажуть, що його отримали множенням 1 на 2 (числа 1 і 2 - комплексні), і записують: = 1 2 . Комплексні 1 і 2 називають множниками. Закони множення комплексних чисел: 1) закон асоціативності ; 2) закон комутативності . Поділ Приватним комплексних чисел називають таке комплексне , що 1 = 1: 2 ( 2 /= 0 ) . Приватне комплексних чисел обчислюють за формулою: =( 1 2 - 1 2 )/( 2 + 2 )+( 1 1 + 2 1 )i/( 2 + 2 ). Про числі кажуть, що його отримали в результаті поділу 1 на 2 , і записують: = 1 / 2 . Додавання і множення комплексних чисел пов'язані правилом, яке називається дистрибутивним закон множення відносно додавання .Тригонометричні комплексні числа
Застосовують також іншу форму запису комплексних чисел, яка називається тригонометричної.1 2 =k 1 k 2 [cos(β1+β2)+isin(β1+β2)]. Приватним тригонометричних комплексних чисел, які не дорівнюють нулю, є комплексне число, модуль якого еквівалентний приватному діленого і дільника (їх модулів), а аргумент еквівалентний різниці аргументів діленого і дільника: 1 / 2 =k 1 /k 2 [cos(β1-β2)+isin(β1-β2)].